Основные типы задач и методы их решения
а) Классификация
1. Расчет электростатических полей в диэлектрических средах. Определение напряженности, индукции и потенциала электростатического поля внутри однородного, изотропного диэлектрика.
Метод решения. Использование теоремы Гаусса для вектора  и соотношения, связывающего между собой
и соотношения, связывающего между собой  и
и  . Воспользоваться аналогичной теоремой для поля
. Воспользоваться аналогичной теоремой для поля  не представляется возможным, поскольку не известен связанный заряд.
не представляется возможным, поскольку не известен связанный заряд.
2. Нахождение напряженности и индукции поля на границе раздела двух сред.
Метод решения. Использование соотношений между нормальными и тангенциальными составляющими векторов  и
и  на границе раздела двух сред.
на границе раздела двух сред.
б) Примеры решения задач
1. Точечный заряд 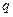 находится в центре шара радиусом
находится в центре шара радиусом 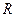 из однородного изотропного диэлектрика проницаемостью
из однородного изотропного диэлектрика проницаемостью 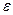 . Найти напряженность поля как функцию расстояния
. Найти напряженность поля как функцию расстояния 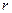 от центра шара. Представить графики зависимостей
от центра шара. Представить графики зависимостей 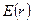 и
и 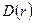 .
.
Решение.
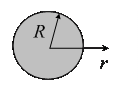 В любой точке поля векторы
В любой точке поля векторы  и
и  направлены радиально. Поток вектора
направлены радиально. Поток вектора  через сферическую поверхность радиусом
через сферическую поверхность радиусом 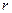
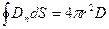 .
.
По теореме Гаусса: 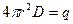 , откуда
, откуда 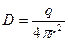 .
.
Так как 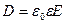 , то
, то
1) для 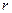 <
< 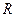 ,
, 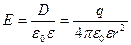 .
.
2) для 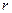 >
> 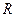 ,
, 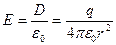 .
.
 Графики зависимостей
Графики зависимостей  и
и  имеют следующий вид:
имеют следующий вид:
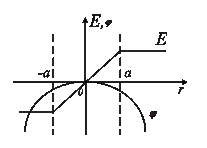
 2. Бесконечно большая пластина из однородного диэлектрика с проницаемостью
2. Бесконечно большая пластина из однородного диэлектрика с проницаемостью 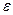 заряжена равномерно сторонним зарядом с объемной плотностью
заряжена равномерно сторонним зарядом с объемной плотностью 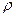 >0. Толщина пластины 2а. Найти
>0. Толщина пластины 2а. Найти 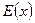 и
и 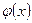 как функции расстояния
как функции расстояния 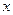 от середины пластины (потенциал в сере
от середины пластины (потенциал в сере 
 дине пластины положить равным нулю). Определить поверхностную плотность связанного заряда.
дине пластины положить равным нулю). Определить поверхностную плотность связанного заряда.
Решение.
Из соображений симметрии ясно, что в середине пластины 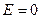 , а во всех остальных точках вектор
, а во всех остальных точках вектор  перпендикулярен поверхности пластины. Воспользуемся теоремой Гаусса для вектора
перпендикулярен поверхности пластины. Воспользуемся теоремой Гаусса для вектора  . В качестве замкнутой поверхности возьмем прямой цилиндр высотой
. В качестве замкнутой поверхности возьмем прямой цилиндр высотой 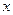 , один торец которого совпадает со средней плоскостью пластины. Пусть площадь сечения этого цилиндра равна
, один торец которого совпадает со средней плоскостью пластины. Пусть площадь сечения этого цилиндра равна 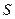 , тогда
, тогда
1) для  :
: 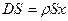 ,
, 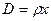 ,
,  ;
;
2) для  :
:  ,
, 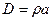 ,
, 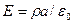 .
.
Используя выражение 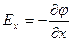 , получаем
, получаем
1) для 
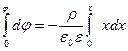 ;
; 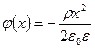 и
и 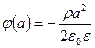 ;
;
2) для 

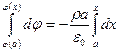 ;
; 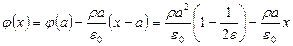 .
.
Графики функции 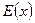 и
и 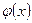 представлены на рисунке.
представлены на рисунке.
Поверхностную плотность связанного заряда определим из выражения
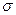 ’=
’= 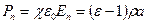 /
/ 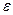 >0.
>0.
Таким образом, если сторонний заряд 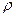 > 0, то на обеих поверхностях пластины будет также положительный связанный заряд.
> 0, то на обеих поверхностях пластины будет также положительный связанный заряд.
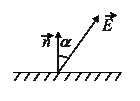
3. Вблизи границы раздела вакуум - диэлектрик напряженность электрического поля в вакууме равна  , причем вектор
, причем вектор 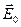 составляет угол
составляет угол 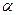 с нормалью к поверхности раздела. Проницаемость диэлектрика
с нормалью к поверхности раздела. Проницаемость диэлектрика 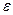 . Найти отношение
. Найти отношение 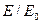 , где
, где 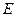 напряженность поля внутри диэлектрика.
напряженность поля внутри диэлектрика.
Решение.
Напряженность поля внутри диэлектрика
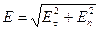 .
.
Воспользовавшись условиями на границе раздела диэлектрика, найдем
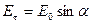 ;
; 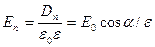 , откуда
, откуда
 < 1, т.е
< 1, т.е 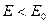 .
.
Дата добавления: 2016-03-22; просмотров: 3556;
