Основные типы задач и методы их решения. 1. Определение емкости уединенного проводника, емкости конденсатора и "батареи" конденсаторов.
а) Классификация
1. Определение емкости уединенного проводника, емкости конденсатора и "батареи" конденсаторов.
Метод решения. Использование соотношений, определяющих емкость уединенного проводника и конденсатора. При этом первоначально определяется с использованием теоремы Гаусса напряженность поля уединенного проводника или конденсатора, при сообщении им некоторого заряда 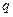 , а затем путем интегрирования выражения
, а затем путем интегрирования выражения  находится приобретаемая разность потенциалов.
находится приобретаемая разность потенциалов.
Для определения емкости "батареи" конденсаторов используются закон сохранения заряда и формула электроемкости конденсатора.
2. Определение энергии взаимодействия точечных зарядов, энергии заряженного проводника и конденсатора, энергии поля, локализованного в заданном объеме.
Метод решения. Использование формул для энергии взаимодействия точечных зарядов, энергии заряженного конденсатора.
Интегрирование выражения для объемной плотности энергии электрического поля:
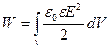 .
.
3. Определение работы при раздвижении пластин конденсатора.
Метод решения.
1) Использование уравнения энергетического баланса при внешнем воздействии на конденсаторы. Работа внешних сил идет на приращение электрической энергии.
2) Непосредственное интегрирование выражения
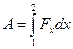 .
.
б) Примеры решения задач
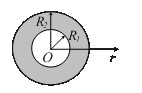 1. Найти емкость шарового проводника радиусом
1. Найти емкость шарового проводника радиусом 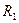 , окруженного примыкающим к нему слоем однородного диэлектрика с наружным радиусом
, окруженного примыкающим к нему слоем однородного диэлектрика с наружным радиусом 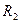 и проницаемостью
и проницаемостью 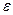 .
.
Решение.
Для нахождения емкости проводника по формуле 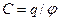 надо мысленно зарядить данный проводник зарядом
надо мысленно зарядить данный проводник зарядом 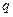 и вычислить его потенциал
и вычислить его потенциал 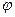 . С этой целью, воспользовавшись теоремой Гаусса для вектора
. С этой целью, воспользовавшись теоремой Гаусса для вектора  , найдем
, найдем 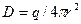 , после чего, с учетом соотношения
, после чего, с учетом соотношения 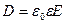 , получим
, получим
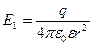 для
для 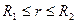 ;
;
 для
для 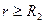 .
.
Зная зависимость 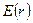 можно непосредственно приступить к нахождению потенциала шара. В. силу различной зависимости
можно непосредственно приступить к нахождению потенциала шара. В. силу различной зависимости 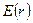 интеграл разбивается на два:
интеграл разбивается на два:
 ;
;
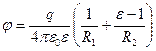 .
.
Окончательно
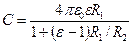 .
.
2. Вычислить энергию взаимодействия четырех одинаковых точечных зарядов q, расположенных в вершинах квадрата со стороной а.
Решение.
Воспользуемся формулой
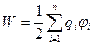 .
.
В данном случае 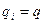 ,
, 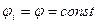 , где
, где 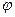 -потенциал в месте нахождения одного из зарядов, обусловленный полем всех остальных зарядов.
-потенциал в месте нахождения одного из зарядов, обусловленный полем всех остальных зарядов.
В соответствии с формулой для потенциала, точечного заряда и принципа суперпозиции найдем
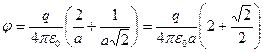 .
.
Окончательно  .
.
3. Заряд 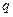 распределен равномерно по объему шара радиусом
распределен равномерно по объему шара радиусом 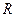 . Полагая диэлектрическую проницаемость всюду равной единице, найти собственную электрическую энергию шара и отношение энергии
. Полагая диэлектрическую проницаемость всюду равной единице, найти собственную электрическую энергию шара и отношение энергии  , локализованной внутри шара, к энергии
, локализованной внутри шара, к энергии  в окружающем пространстве.
в окружающем пространстве.
Решение.
Прежде всего найдем с помощью теоремы Гаусса напряженность поле внутри и вне шара
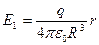
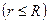 ;
;
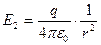
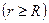 .
.
Объемная плотность энергии будет также являться функцией расстояния:
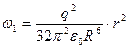
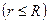 ;
;
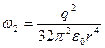
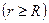 .
.
Поскольку зависимость 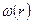 различна для областей пространства внутри и вне шара, то нахождение полной энергии электрического поля разбивается на два интеграла
различна для областей пространства внутри и вне шара, то нахождение полной энергии электрического поля разбивается на два интеграла

где 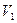 - объем пространства, занимаемый зарядом;
- объем пространства, занимаемый зарядом;
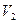 - объем остального пространства.
- объем остального пространства.
Объем 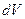 следует выбрать в виде тонкого шарового слоя толщиной
следует выбрать в виде тонкого шарового слоя толщиной 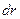 (в пределах такого объема
(в пределах такого объема 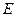 и
и  постоянны):
постоянны):
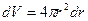 .
.
Подставляя выражения для  и
и 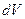 и проводя интегрирование, получаем
и проводя интегрирование, получаем 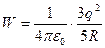 .
.
Аналогично найдем, что 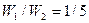 т.е не зависит от радиуса шара.
т.е не зависит от радиуса шара.
4. Плоский воздушный конденсатор (S=200  , d1=0,3см) заряжен до разности потенциалов
, d1=0,3см) заряжен до разности потенциалов 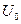 = 600 В. Какую работу надо совершить, чтобы увеличить расстояние между обкладками до
= 600 В. Какую работу надо совершить, чтобы увеличить расстояние между обкладками до 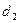 =0,5см, не отключая конденсатор от источника.
=0,5см, не отключая конденсатор от источника.
Решение.
Первый способ.
Конденсатор соединен с источником, поэтому при любых манипуляциях разность потенциалов на его зажимах остается постоянной и равной 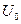 , при этом заряд может изменяться. При раздвижении пластин внешняя сила равна и противоположна силе взаимодействия и ее работа
, при этом заряд может изменяться. При раздвижении пластин внешняя сила равна и противоположна силе взаимодействия и ее работа
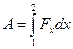 .
.
Поскольку поле, создаваемое каждой из пластин, на небольших расстояниях однородно, то
 ,
,
где  - напряженность поля, создаваемого одной из пластин;
- напряженность поля, создаваемого одной из пластин; 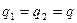 - абсолютное значение заряда пластин. Напряженность поля, созданного одной пластиной, вдвое меньше напряженности между обкладками конденсатора и равна
- абсолютное значение заряда пластин. Напряженность поля, созданного одной пластиной, вдвое меньше напряженности между обкладками конденсатора и равна
 .
.
Подставляя найденные соотношения в выражение для силы, получаем
 .
.
При раздвижении обкладок 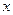 изменяется в пределах от
изменяется в пределах от  до
до 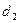 , тогда
, тогда
 .
.
Второй способ.
В соответствии с уравнением энергетического баланса
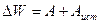 ,
,
где 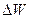 - изменение энергии конденсатора;
- изменение энергии конденсатора; 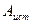 - работа, совершаемая источником.
- работа, совершаемая источником.
Так как 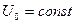 изменение заряда конденсатора
изменение заряда конденсатора
 , откуда
, откуда 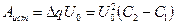 .
.
Изменение энергии конденсатора найдем по формуле
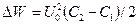 .
.
где 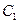 и
и 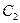 - соответственно конечная и начальная емкости конденсатора.
- соответственно конечная и начальная емкости конденсатора.
Из уравнения энергетического баланса с учетом того, что 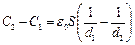 , Окончательно получим
, Окончательно получим
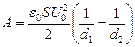 .
.
Дата добавления: 2016-03-22; просмотров: 1089;
