Основные типы задач и методы их решения. 1. Определение напряженности и потенциала заданного распределения точечных зарядов.
а) Классификация
1. Определение напряженности и потенциала заданного распределения точечных зарядов.
Метод решения. Прямое суммирование выражений для потенциала и напряженности электростатического поля каждого заряда из заданного распределения точечных зарядов:
 ;
; 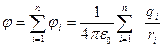
2.Определение потенциала и напряженности электростатического поля заданного непрерывного распределения линейных, поверхностных или объемных зарядов.
Метод решения. Интегрирование выражений для потенциала и напряженности поля заданного непрерывного распределения заряда:
 ;
;  ,
,
где  ,
, 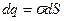 или
или  .
.
3. Определение напряженности электростатического поля и потенциала заданного непрерывного распределения зарядов, обладающих плоской, осевой или центральной симметрией.
Метод решения. Применение теоремы Гаусса и формулы, связывающей напряженность поля и потенциал:
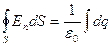 ;
;  .
.
б) Примеры решения задач
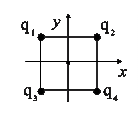
I. В вершинах квадрата со стороной 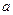 находятся точечные заряды
находятся точечные заряды 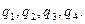 Определить напряженность электростатического поля и потенциал в центре квадрата. Рассмотреть случаи, когда:
Определить напряженность электростатического поля и потенциал в центре квадрата. Рассмотреть случаи, когда:
а)  ;
;
б) 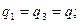
 ;
;
в) 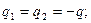
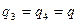 .
.
|
Решение.
Напряженность поля и потенциал системы точечных зарядов определяются соотношениями
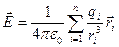 ;
; 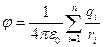
Учитывая, что  :
:
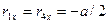 ,
, 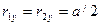 ,
,
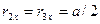 ,
, 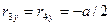 ,
,
получаем 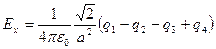 ,
,
 ,
,
 ,
,  ;
;
а) если  , то
, то
 ,
, 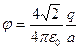 ;
;
б) если 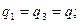
 , то
, то
 ,
, 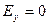 ,
, 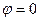 ;
;
в) если 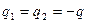 ;
; 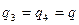 , то
, то
 ,
, 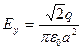 ,
, 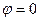 .
.
2. Положительный заряд равномерно распределен по тонкому кольцу радиусом 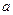 с линейной плотностью
с линейной плотностью 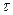 . Найти напряженность
. Найти напряженность 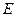 электрического поля на оси кольца как функцию расстояния x от его центра. Исследовать случаи:
электрического поля на оси кольца как функцию расстояния x от его центра. Исследовать случаи:
 а)
а) 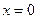 , б)
, б) 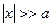 .
.
Решение.
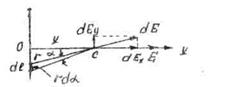
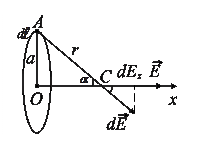
Выделим на кольце около точки А элемент 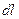 . Выражение для
. Выражение для 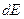 от этого элемента в точке С:
от этого элемента в точке С:
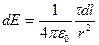 .
.
В силу симметрии вектор  направлен по оси x, следовательно,
направлен по оси x, следовательно, 
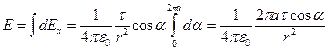 .
.
Учитывая, что 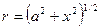 и
и 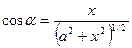 ,
,
получаем 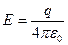
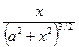 .
.
а) Если 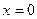 , то
, то 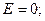 б) если
б) если 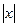 >>a, то
>>a, то  ,
,
т.е. на больших расстояниях эта система ведет себя как точечный заряд.
3. Тонкая прямая нить длиной 2 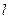 заряжена равномерно с линейной плотностью
заряжена равномерно с линейной плотностью 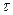 . Найти напряженность
. Найти напряженность 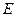 поля в точке, отстоящей на расстоянии x от центра нити и расположенной симметрично относительно ее концов. Исследовать случаи: a) x>>
поля в точке, отстоящей на расстоянии x от центра нити и расположенной симметрично относительно ее концов. Исследовать случаи: a) x>> 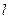 ; б)
; б) 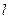

 .
.
Решение.
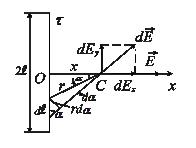 Напряженность поля, создаваемого элементом
Напряженность поля, создаваемого элементом 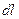 , равна
, равна
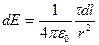 .
.
Из соображений симметрии ясно, что
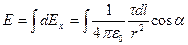 .
.
Приведем это выражение к виду, удобному для интегрирования. Из рисунка видно, что
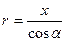 ;
; 
Поэтому  ,
,
где  .
.
Окончательно имеем
 .
.
а) Если х>> 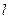 , то
, то 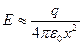 как поле точечного заряда; б) Если
как поле точечного заряда; б) Если 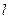

 , то
, то 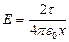 .
.
4. Очень тонкий диск равномерно заряжен с поверхностной плотностью 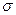 >0. Найти напряженность электрического поля на оси этого диска в точке, из которой диск виден под телесным углом
>0. Найти напряженность электрического поля на оси этого диска в точке, из которой диск виден под телесным углом 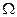 .
.
Решение.
 Из соображений симметрии ясно, что вектор
Из соображений симметрии ясно, что вектор  на оси диска должен совпадать с направлением этой оси. Поэтому достаточно найти составляющую
на оси диска должен совпадать с направлением этой оси. Поэтому достаточно найти составляющую 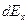 в точке А от элемента заряда на площади
в точке А от элемента заряда на площади  и затем проинтегрировать это выражение по всей поверхности диска:
и затем проинтегрировать это выражение по всей поверхности диска:
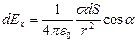 .
.
В данном случае 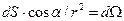 - телесный угол, под которым площадка
- телесный угол, под которым площадка  видна из точки А, и с учетом этого
видна из точки А, и с учетом этого
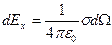 ;
;  .
.
Заметим, что на больших расстояниях от диска
 ,
,
где 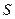 - площадь диска. Тогда
- площадь диска. Тогда 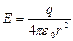 как поле точечного заряда
как поле точечного заряда 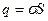 .
.
В непосредственной же близости от точки 0 телесный угол 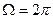 и
и  .
.
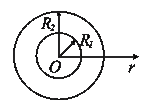
5. Две концентрические сферы с радиусами 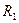 и
и 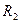 (
( 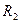 >
> 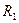 ) равномерно заряжены с поверхностными плотностями
) равномерно заряжены с поверхностными плотностями 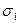 и
и 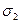 . Найти выражение для напряженности и потенциала электростатического поля как функции расстояния
. Найти выражение для напряженности и потенциала электростатического поля как функции расстояния 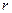 от центра сфер.
от центра сфер.
 Решение.
Решение.
Поле такой системы центрально-симметричное, поэтому используем теорему Гаусса и в качестве замкнутой поверхности выберем концентрическую сферу радиусом 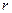 .
.
Для 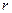 <
< 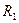 :
: 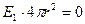 и
и  .
.
Для 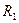 <
< 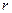 <
< 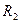 :
: 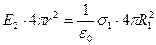 и
и 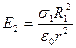 .
.
Для 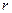 >
> 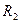 :
:  .
.
и 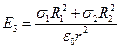 .
.
Для определения потенциала используем связь между 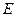 и
и 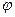 в сферических координатах:
в сферических координатах:
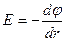 и
и 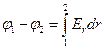 .
.
Для 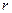 >
> 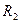 :
:  ,
,  ,
,
 .
.
Для 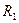 <
< 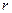 <
< 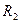
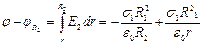 ,
,
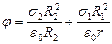 ;
;  .
.
Для 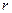 <
< 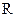 1:
1: 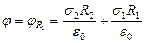 .
.
Дата добавления: 2016-03-22; просмотров: 2372;
