Способы записи ФАЛ.

Основными способами описания ФАЛ являются: словесная форма, таблицы истинности, математическое описание и описание кубическими комплексами.

Словесная формаявляется наиболее простой и используется на начальных этапах анализа и проектирования цифровых устройств. Она отражает те свойства, которым это устройство должно отвечать.

Упражнение 7.1. ФАЛ трех переменных равна единице, если хотя бы две входные переменные равны единице.

Таблицы истинностиявляются наиболее простой формой формализации алгоритма функционирования цифрового устройства. Она содержит все возможные комбинации входного кода 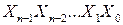с соответствующими ими значениями выходного кода 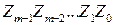. Поэтому она содержит 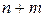столбцов и 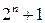строк.

Упражнение 7.2. Записать таблицу истинности для ФАЛ из упражнения 7.1.

Решение.

Описанное устройство содержит 3 входа и 1 выход. Для трех входных переменных 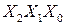возможно 8 различных комбинаций входного кода. Сведем их в левую часть таблицы. В правой части запишем соответствующие значения выходного кода .

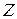Таблица 7.4. Таблица истинности для упражнения 7.2.

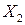
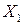
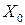
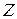
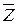
Математическое описаниеэто форма, наиболее точно соответствующая данному определения ФАЛ, так как содержит связь входных и выходных переменных логического устройства, выраженную через основные функции алгебры логики. Классическими являются совершенная дизъюнктивная и совершенная конъюнктивная формы записи.

Совершенной дизъюнктивной нормальной формой (СДНФ) называется логическая сумма элементарных логических произведений, в каждое из которых входят все аргументы или их инверсии. Каждое произведение этой суммы принято называть конституентой единицы.

СДНФ может быть легко получена из таблицы истинности с использованием следующего алгоритма:

а) для каждого набора переменных, на котором ФАЛ равна единице, записывают элементарные логические произведения входных переменных (конституенты единицы), причем переменные, равные нулю, записывают с инверсией;

б) логически суммируют все конституанты единицы.

Упражнение 7.3. Для таблицы истинности из упражнения 7.2 записать СДНФ.

Решение.

Из таблицы 7.4. следует, что функция равна единице на четырех наборах переменных. Записываем четыре конституенты единицы и логически суммируем их:

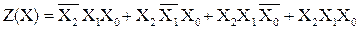
Совершенной конъюнктивной нормальной формой (СКНФ) называется логическое произведение элементарных логических сумм, в каждую из которых все аргументы или их инверсии входят один раз. Каждую сумму этого произведения принято называть конституентой нуля.

СКНФ может быть легко получена из таблицы истинности с использованием следующего алгоритма:

а) для каждого набора переменных, на котором ФАЛ равна нулю, записывают элементарные логические суммы входных переменных (конституенты нуля), причем переменные, значения которых равны единице, записывают с инверсией;

б) логически перемножают все полученные конституанты нуля.

Упражнение 7.4. Для таблицы истинности из упражнения 7.2 записать СКНФ.

Решение.

Из таблицы 7.4. следует, что функция равна нулю на четырех наборах переменных. Записываем четыре конституенты нуля и логически перемножаем их:

.

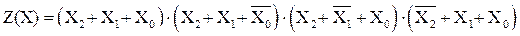Рассмотренный подход позволяет получить выражения для самой функции. В ряде случает удобнее записать ФАЛ не для функции для ее инверсии. При этом используют те же алгоритмы.

Упражнение 7.5. Для таблицы истинности из упражнения 7.2 записать СДНФ и СКНФ инверсной функции.

Решение.

Добавим в таблицу 7.4. столбец с инверсными значениями функции и для него запишем соответствующие выражения:

СДНФ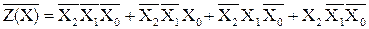

СКНФ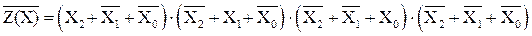

Кубические комплексы используют отображение ФАЛ в виде совокупности 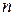-мерных векторов, каждая координата которых принимает только два значения 0 или 1. Вершины этих векторов геометрически можно представить как вершины 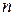-мерного куба. Их число соответствует совокупности всех возможных комбинаций входной переменной, записанной в двоичной системе счисления. На рис.7.2. для трехразрядного кода 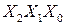представлена графическая интерпретация такого представления. Если перечислить все вершины куба, соответствующие единичным значениям функции, то получим описание ФАЛ через совокупность его конституент единицы, подобное СДНФ. При этом коды, соответствующие конституентам единицы могут быть выражены в произвольной системе счисления. Такая запись носит название нулевого кубического комплекса ( 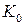) функции.

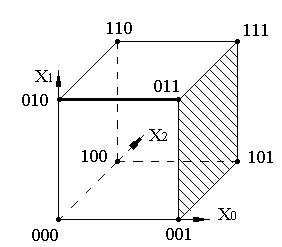
Рис.7.2. Геометрическая интерпретация кубического представления ФАЛ.

Очевидно, что вершины, лежащие на ребрах куба, всегда отличаются только одной переменной, а их коды – только в одном разряде. Коды, отличающиеся только в одном разряде, назовем соседними. Поэтому характеризуя положение этого ребра несовпадающую координату можно опустить. Таким образом, два куба из нулевого комплекса могут образовать новый куб, именуемый единичным кубом. Его характерной особенностью является исключение из описания одной переменной. Например (см. рис.7.2.), соседние ноль кубы 011 и 010 не совпадают только по младшей координате 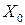. Поэтому образованное ими ребро (на рисунке выделено жирным) можно описать только двумя переменными - 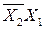. То есть описание ребер уже не является набором конституент единицы ФАЛ. Совокупность единичных кубов образует единичный кубический комплекс ( 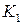) ФАЛ (комплекс ранга 1).

Рассуждая аналогично можно сказать, что описывая грани куба, можно опустить еще одну несовпадающую координату. Соответствующий ей код будет содержать уже на две переменных меньше. Например, грань, образованная ноль кубами 001, 011, 111 и 101 (см. рис.7.2., грань заштрихована) образуют четыре единичных куба 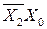, , 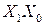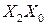и и 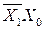только один единичный куб 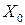. Совокупность таких кодов образует двоичный кубический комплекс ( 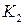) ФАЛ (комплекс ранга 2).

В 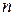-мерном пространстве так можно рассуждать вплоть до получения описания, состоящего только из одной координаты (переменной), создавая при этом кубические комплексы все более высокого ранга.

Объединяя существующие кубические комплексы 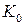, , 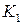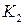и так далее, получим кубический комплекс ФАЛ ( 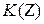), являющийся ее описанием.

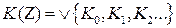(7.2)

Из вышесказанного следует, что нулевой кубический комплекс всегда однозначно определяет исходную ФАЛ. В комплексы более высоких рангов могут входить не все кубы нулевого комплекса, поэтому эти комплексы не всегда однозначно определяют исходную ФАЛ.

Заметим, что в записи соответствующих кубов, обычно сохраняется позиционность расположения переменных. Поэтому, вместо отсутствующих переменных в записи куба ставится, например, прочерк, или другой символ. Такое представление удобно при обработке ФАЛ на ЭВМ.

Упражнение 7.6. Представить ФАЛ, соответствующую таблице истинности из упражнения 7.2, в виде кубического комплекса.

Решение.

Данная функция содержит 4 конституенты единицы, поэтому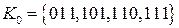

Ранее отмечалось, что запись кодов конституент единицы может быть выполнена в любой системе счисления. Например, в десятичной системе счисления для нулевого кубического комплекса можно записать .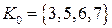

Ноль кубы комплекса 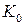образуют три куба ранга 1 и .

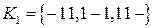Кубы из комплекса 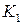не образуют кубы ранга 2. Поэтому для заданной ФАЛ кубический комплекс имеет вид: .

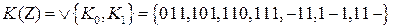На рис.7.3. показана графическая интерпретация кубов комплекса 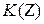функции.

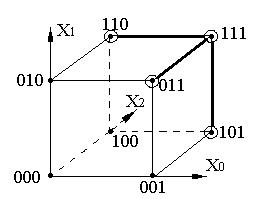
Рис.7.3. Графическая интерпретация кубических комплексов из упражнения 7.6: 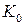- отмечены окружностями, 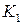- жирными линиями.