Логические основы цифровых устройств.

Напомним, что в отличие от аналоговых и импульсных устройств, преобразующих сигналы, поставленные в соответствие некоторым физическим величинам, цифровые устройства преобразуют числа (коды), поставленные в соответствие этим физическим величинам. Эти коды получаются путем выборки по заданному алгоритму (например, дискретизации по времени и квантованию по уровню) некоторого конечного числа значений исходной величины и присвоения этим значениям некоторого числового эквивалента, который, в общем случае, может быть никак не связан с самой описываемой физической величиной. При этом встает два важных вопроса. Как записывать эти числа, и каким образом их можно представить для обработки средствами электроники. Решение этих вопросов существенно влияет на методологию построения цифровых устройств.

7.1. Позиционная система счисления.В настоящее время для записи чисел наибольшее распространения получила позиционная система счисления, оперирующая ограниченным числом символов (цифр), в которой значимость конкретной цифры определяется ее расположением (разрядом) в записи числа. Общий формат записи 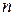-разрядного положительного целого числа 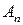в этой системе можно представить в следующем виде:

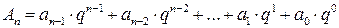, (7.1)

где: 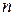- целое число (количество разрядов);

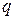- основание системы счисления;

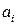- разрядные коэффициенты, принимающие 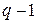значение;

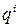- весовые коэффициенты.

Если из записи числа (7.1) удалить весовые коэффициенты и знаки сложения, получим сокращенную запись числа, называемую 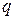-ичным кодом числа. Для записи дробного числа показатели весовых коэффициентов 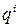должны быть отрицательными ( ).

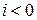В таблице 7.1 приведено представление десятичного числа 99 в позиционных системах с различным основанием.

Таблица 7.1. Представление числа в различных системах счисления

Основание системы счисления	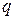Запись (код) числа

Примечание: В шестнадцатеричной системе счисления ( 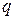=16) используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C. D, E, F.

Из таблицы следует, что чем меньше значение основания системы счисления и, следовательно, чем меньше значений может принимать один разряд числа, тем больше разрядов необходимо для записи заданного числа.

Предположим, что при построении цифрового устройства каждый разряд числа будет ассоциироваться с выходным сигналом некоторого элементарного электронного блока. Тогда каждому разрядному коэффициенту числа необходимо будет поставить в соответствие некоторое значение параметра электрического сигнала (в простейшем случае ток или напряжение), формируемого на выходе этого блока. То есть каждый элементарный электронный блок должен будет формировать на выходе 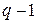значение электрического сигнала.

Очевидно, что чем меньше основание используемой системы счисления, тем больше потребуется элементарных электронных блоков, но каждый из них должен будет формировать меньшее число выходных сигналов, что, скорее всего, приведет к его упрощению. Таким образом, имеем некоторую оптимизационную задачу. Увеличение 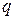ведет к уменьшению числа необходимых элементарных электронных блоков, но усложняет их. Следовательно существует такое 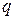для которого общие материальные затраты на реализацию устройства будут минимальными.

Однако при решении этой задачи необходимо учитывать тот факт, что уменьшение числа различных уровней выходных сигналов повысит надежность их идентификации, тот есть надежность работы всего устройства. Действительно, если, например, максимальное значение выходного напряжения составляет 5 вольт и нам необходимо сформировать 10 уровней выходного напряжения ( 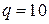), эти уровни будут отличаться на 0.5 вольта. Если число требуемых выходных уровней только два, то вероятность их идентификации во много раз возрастает. Это условие является ограничением при решении задачи нахождения оптимального значения .

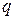Решением этой задачи является использование при разработке цифровых устройств двоичной системы счисления ( 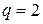) при которой разрядные коэффициенты числа могут принимать только два значения «0» или «1». Полученный таким образом код числа называется прямым двоичным кодом.

7.2. Математическое описание цифровых устройств. Для описания и анализа работы цифровых устройств используется разработанный в 19 веке английским математиком Джорджем Булем аппарат математической логики (алгебры логики). Этот аппарат оперирует двумя понятиями: событие истинно и событие ложно, которым можно поставить в соответствие два разрядных коэффициента двоичной системы счисления. Поэтому цифровые устройства часто называют логическими, а сами весовые коэффициенты – логическим нулем (лог. «0») и логической единицей (лог. «1»).

Возможно два варианта сопоставления событий и логических переменных. Первый, так называемая положительная логика, предполагает сопоставление истинности события логической единице, а ложности события – логическому нулю. Второй, так называемая отрицательная логика, сопоставляет истинность события с логическим нулем, а его ложность – с логической единицей.

Далее будем пользоваться понятием положительной логики (истинность – лог. «1», ложность – лог. «0»).

Алгебра логики предполагают выполнение над логическими переменными трех основных операций: логического сложения, логического умножения и отрицания.