Принцип двойственности и функционально полная система логических элементов.
Принцип двойственности определяет взаимосвязь логических операций И и ИЛИ. Он формулируется следующими условиями:
Если 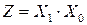 , то и
, то и 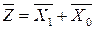 , (7.5)
, (7.5)
Если 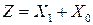 , то
, то  . (7.6)
. (7.6)
Введем понятие функционально полной системы логических элементов. Функционально полной называется совокупность логических элементов, позволяющая реализовать логическое устройство произвольной сложности.
Очевидно, что элементы И, ИЛИ и НЕ образуют функционально полную систему логических элементов. Так как согласно принципа двойственности операции И и ИЛИ взаимопреобразуемы, то функционально полными являются системы из двух элементов. Это И, НЕ и ИЛИ, НЕ. Ранее мы показали, что использование параллельной схемы преобразователя сигнала позволяет совместить в одном элементе выполнение двух операций И и НЕ или ИЛИ и НЕ (см. рис.7.5). Поэтому можно утверждать, что и один элемент И-НЕ или ИЛИ-НЕ составляют функционально полную систему логических элементов.
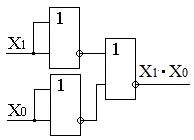
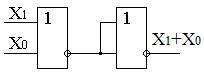
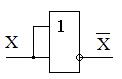
В качестве примера, в таблице.7.5 показана реализация основных логических операций с использованием только одного элемента И-НЕ и ИЛИ-НЕ
Таблица 7.5. Реализация основных логических операций
с использованием штриха Шеффера и стрелки Пирса
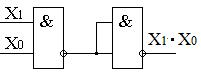
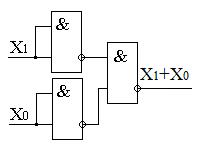
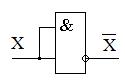
| Операция | И | ИЛИ | НЕ |
Штрих Шеффера
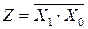
| 
| 
| 
|
Стрелка Пирса
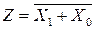
| 
| 
| 
|
Дата добавления: 2016-03-10; просмотров: 745;
