Табличный метод минимизации.
Данный метод базируется на табличном представлении ФАЛ. Ранее мы показали, что два куба ранга ноль образуют куб ранга один только в том случае, когда соответствующие им коды отличаются только в одном разряде. Такие коды мы назвали соседними. Если составить таблицу, в которой рядом расположенным клеткам поставить в соответствие соседние коды и в эти клетки записать соответствующие значения ФАЛ, получим аналог таблицы истинности. Однако теперь объединение двух соседних клеток фактически означает выделение ребра, объединение четырех рядом расположенных клеток эквивалентно выделению грани куба и так далее. Таким образом, если в полученной таблице выделять прямоугольные области, содержащие 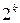 , где
, где 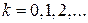 клеток, получим кубы ранга
клеток, получим кубы ранга 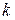 . Для получения МДФ остается только выбрать минимальное число максимально больших областей, охватывающих все выбранные значения функции и просуммировать соответствующие им коды. Такое табличное представление ФАЛ получило название карт Вейча или Карно. На рис.7.11 приведены карты Вейча для функций 2, 3 и 4 переменных.
. Для получения МДФ остается только выбрать минимальное число максимально больших областей, охватывающих все выбранные значения функции и просуммировать соответствующие им коды. Такое табличное представление ФАЛ получило название карт Вейча или Карно. На рис.7.11 приведены карты Вейча для функций 2, 3 и 4 переменных.
 а)
а)
|  б)
б)
|  в)
в)
|
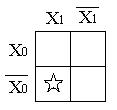
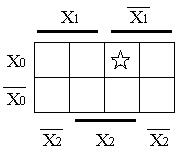
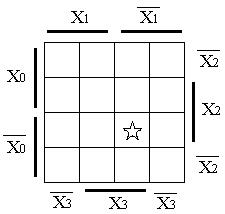
Рис.7.11. Карты Вейча для функций 2 а), 3 б) и 4 в) переменных.
Принцип записи переменных вокруг карты базируется на том, что для половины входных кодов любая переменная принимает значение 1, а для другой половины – 0. Порядок чередования переменных при этом не имеет значения. Так клетка, отмеченная звездочкой, для рис.7.11.а) соответствует коду 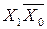 , для карты рис.7.110.б) – коду
, для карты рис.7.110.б) – коду 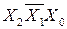 , а для рис.7.11. в) – коду
, а для рис.7.11. в) – коду 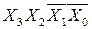 .
.
Методику получения МДФ с помощью карт Вейча можно представить в следующем виде:
- на карте Вейча ФАЛ выделяют прямоугольные области и объединяют клетки с выбранным значением функции «лог 1» или «лог. 0». Каждая область должна содержать 2k клеток, где k - целое число (0, 1, 2,…). Выделенные области могут пересекаться, т. е. одна клетка может входить в несколько различных областей;
- каждая из выделенных областей является 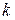 кубом ФАЛ и описывается произведением переменных, которые для этой области остаются неизменными. Каждое произведение должно содержать n – k переменных;
кубом ФАЛ и описывается произведением переменных, которые для этой области остаются неизменными. Каждое произведение должно содержать n – k переменных;
- из полученного множества выбирают минимальное число максимально больших областей, включающих все выбранные значения ФАЛ;
- логически суммируют выбранные произведения.
При выборе единичных значений ФАЛ получаем саму функцию, а при выборе нулевых значений – ее инверсию.
Следует отметить, что карты Вейча 3 и 4 переменных фактически не являются плоскими фигурами. Карта для 3 переменных это поверхность цилиндра, а для 4 переменных – поверхность тора. Поэтому клетки, расположенные в крайних столбцах и строках карт так же являются соседними и могут образовывать самостоятельные области.
Упражнение 7.9. С помощью карт Вейча найти МДФ для ФАЛ соответствующей таблице истинности из упражнения 7.2.
Решение.
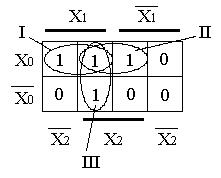
| Заполним карту Вейча для заданной ФАЛ. Согласно таблице истинности четыре клетки таблицы заполнены единичными значениями и четыре нулевыми. Выберем единичные значения и объединим их в области. Имеем три области, причем клетка, соответствующая коду 111 входит во все области. Для области I неизменными остаются переменные 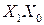 . Для области II неизменны . Для области II неизменны 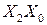 , а для области III - , а для области III - 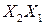 / Суммируя полученные коды получим: / Суммируя полученные коды получим:
|
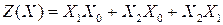 .
.
Это выражение соответствует ранее полученному в упражнении7.8ю
Выберем нулевые значения функции. В этом случае так же имеем три области: 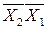 ,
, 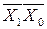 и
и 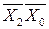 . Этим областям соответствует МДФ вида:
. Этим областям соответствует МДФ вида: 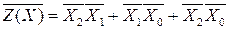 .
.
Дата добавления: 2016-03-10; просмотров: 1276;
