Общий подход к минимизации ФАЛ

Ранее мы показали, что техническая реализация логического устройства может быть выполнена с применением ее ФАЛ. Однако использование для этой цели выражений в виде СДНФ или СКНФ приводит к неоправданному усложнению устройства. Поэтому первоначально полученную ФАЛ необходимо минимизировать. Целью минимизации является упрощение технической реализации устройства, которую можно связать с уменьшением числа и упрощением (уменьшением числа входов) используемых логических элементов. Наиболее просто решить эту задачу можно с применением кубического представления ФАЛ. В разделе 7.2.3. было показано, что ФАЛ можно описать не только перечислением ее конституент, соответствующих вершинам 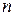-мерного куба, но и перечислением его ребер, граней и т.д. При этом число членов в выражении сокращается. Таким образом, задача минимизации ФАЛ сводится к отысканию такой совокупности кубов, которая, во-первых, содержит все ноль кубы функции и, во-вторых, эти кубы должны иметь максимально возможный ранг. Такая совокупность кубов называется минимальным покрытием или покрытием минимальной стоимости ФАЛ. Этому покрытию соответствует минимальная дизъюнктивная форма (МДФ) ФАЛ, получаемая суммированием произведений переменных, соответствующих выбранным кубам. Таким образом, минимизация ФАЛ сводится в выбору из его кубического комплекса покрытия минимальной стоимости, включающего все кубы ранга ноль исходной ФАЛ.

Упражнение 7.8. Найти покрытие минимальной стоимости и МДФ для кубического комплекса из упражнения из упражнения 7.6.

Решение.

Полученный кубический комплекс ФАЛ имеет вид:

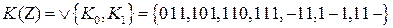. В него входят кубы рангов 0 и 1. Из рисунка 7.3. следует, что единичный кубический комплекс 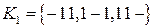полностью включает все ноль кубы исходной функции. Так как этот комплекс не образует кубы более высокого ранга, то он и является покрытием минимальной стоимости ФАЛ.

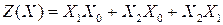
Очевидно, что полученное выражение содержит в 2 раза меньше членов, чем исходное и его техническая реализация будет проще. Приведем полученное выражение к базису элементов 2И-НЕ и построим его схему. Схема разработанного устройства приведена на рис.7.9. Сравнение этой схемой с полученной ранее (см. рис.7.8) показывает, что минимизация ФАЛ позволила значительно упростить техническую реализацию логического устройства.

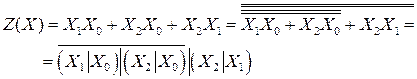
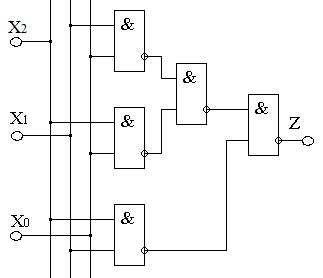
Рис.7.10. Логическая схема устройства из упражнения 7.8.

Процесс нахождения кубического комплекса ФАЛ и выделения из него покрытия минимальной стоимости легко реализуется на ЭВМ. Однако при ручной минимизации необходимы более наглядные методы его отыскания. Такой метод в 1952 году был предложен американским ученым Эдвардом Вейчем и год спустя усовершенствован Морисом Карно.