Лекции № 5, 6. Основные уравнения подземной гидромеханики.

Рассматривается процесс, для которого температура флюидов равна температуре пласта (изотермический процесс).

В число дифференциальных уравнений фильтрации входят уравнение баланса массы в элементе пористой среды – уравнение неразрывности, дифференциальное уравнение движения – закон Дарси в дифференциальной форме, а также уравнения состояния флюида и пористой среды.

Уравнение неразрывности потока

Уравнение неразрывности (сплошности) фильтрационного потока для однородного сжимаемого флюида в деформируемой пористой среде представляет собой уравнение баланса массы в элементарном объеме пористой среды.

Математически это выражается следующим образом. Рассматривается прямоугольный параллелепипед со сторонами dx, dy, dz, параллельных осям координат X, Y, Z соответственно. В единицу времени в параллелепипед по направлению по оси X входит масса 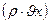dy·dz, а с противоположной стороны выходит масса, равная:

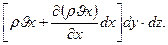
За время dt разность (изменение массы флюида между массами, которые входят и выходят в направлении оси X), равна:

-

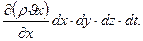
Для направлений, параллельных осям Y и Z аналогично получим:

- -

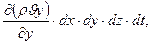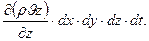
Общее изменение массы во всем объеме за время dt равно:

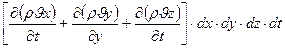- (1)

С другой стороны, масса флюида рассматриваемого элемента равна 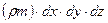. Изменение массы за время dt выражается как

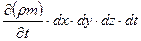(2)

Приравняв (1) и (2), получим

- (3)

Уравнения состояния флюидов и пористой среды

Закон Дарси в дифференциальной форме и уравнение неразрывности потока содержит плотность ρ, коэффициент пористости m, коэффициент проницаемости k.

При изотермическом процессе зависимость плотности однородного флюида от давления представляет собой уравнение состояния.

1. При установившейся фильтрации капельной жидкости можно считать ее плотность независящей от давления, т.е. рассматривать жидкость как несжимаемую. Тогда,

ρ=const. (4)

2. Соотношение между плотностью к давлению для сжимаемой жидкости может быть получено, исходя из уравнения, определяющего коэффициент сжимаемости жидкости βж:

βж= - 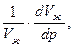(5)

где, Vж – начальный объем жидкости.

Если массу рассматриваемого объема жидкости обозначим через М,

то Vж=М/ρ и 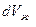= 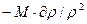и уравнение (5) принимает вид : βж= 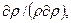откуда после интегрирования получим:

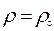
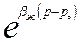(6)

Природные газы можно считать идеальными, если пластовые давления газовых месторождений невелики (до 6-9 МПа) и депрессия до 1 МПа.

Уравнением состояния идеального газа является уравнение Клайперона-Менделеева

P/ρ=RT

где, R – газовая постоянная.

Если 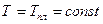, а - плотность газа при атмосферном давлении, то уравнение состояния идеального газа принимает вид:

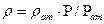(7)

Для газовых месторождений с высоким пластовым давлениями (до 40-60 МПа), эксплуатирующихся с большими депрессиями (15-30 МПа), используется уравнение состояния реального газа:

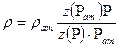(8)

где z – коэффициент сверхсжимаемости газа.

4. Вследствие малой деформации твердой фазы считают обычно, что изменение пористости зависит от изменения давления линейно. Вводя коэффициент объемной упругости пласта 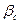, закон сжимаемости породы записывают в виде:

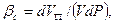(9)

где 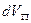– изменение объема пор в элементе пласта, имеющим объем V, при изменении давления на dp. Закон сжимаемости (9) можно записать в виде:

dm=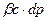

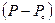или m= m +β_с (10)

При малых изменениях давления, зависимость проницаемости от давления можно принять линейной

,

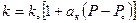а при больших – экспоненциальной

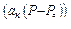k = k e (11)

где, 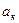– коэффициент, определяемый экспериментально, зависит от состава породы.

Основная литература: 2 [39-49]

Дополнительная литература: 4 [44-51]

Контрольные вопросы:

1. Уравнение неразрывности потока.

2. Уравнение движения флюида.

3. Уравнение состояния флюида.

4. Уравнение состояния породы.

5. Коэффициент объемного расширения жидкости.

6. Коэффициент сжимаемости породы.