Лекции № 8, 9. Установившееся движение несжимаемой жидкости по закону Дарси
Дифференциальное уравнение установившейся фильтрации несжимаемой жидкости.
Если жидкость несжимаема, то ее уравнение состояния 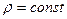 . Также пористость m=const. Тогда уравнение неразрывности потока примет вид:
. Также пористость m=const. Тогда уравнение неразрывности потока примет вид:

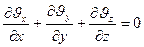 (1)
(1)
Подставляя в (1) V 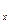 , V
, V 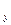 , V
, V  , получим
, получим
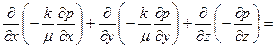 0
0
или
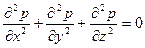 (2)
(2)
Расчет основных гидродинамических характеристик одномерного прямолинейно-параллельного фильтрационного потока.
Пусть в горизонтальном пласте постоянной толщины h и ширины В на контуре питания поддерживается постоянное давление P 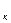 , а на добывающей галерее, отстоящей на расстоянии Lк от контура питания (КП), постоянное давление P
, а на добывающей галерее, отстоящей на расстоянии Lк от контура питания (КП), постоянное давление P  . Направляем ось координат ОХ вдоль линии тока, ось OY вдоль КП.
. Направляем ось координат ОХ вдоль линии тока, ось OY вдоль КП.
Так как меняется только координата Х, то уравнение (2) принимает вид:
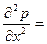 0 (3)
0 (3)
которое, решается при следующих граничных условиях
P=P 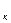 при x=0;
при x=0;
P=P 
 при x=L
при x=L 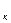 (4)
(4)
Дважды интегрируя (3) и удовлетворяя условиям (4) получим закон распределения давления в пласте:
P=P 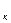 -
- 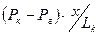 (5)
(5)
найдем градиент давления 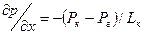
Тогда скорость фильтрации
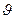 =
=  (6)
(6)
Дебит галереи определяется выражением
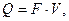
где, F=Bh – площадь поперечного сечения пласта.
с учетом (6) получим, что
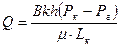 (7)
(7)
Закон движения частицы жидкости найдем по формуле:
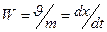
 (8)
(8)
Разделяя переменные и учитывая (6), получим после интегрирования
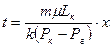 (9)
(9)
Время полного выбора жидкости из пласта (Т) определяется по (9) при x=L 
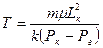 (10)
(10)
Средневзвешенное по объему пластовое давление (Р) найдем по формуле:
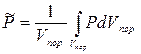 (11)
(11)
где, V  =BhLкm, dV
=BhLкm, dV  = Bhmdx (12)
= Bhmdx (12)
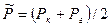 (13)
(13)
3. Расчет основных гидродинамических характеристик одномерного плоскорадиального фильтрационного потока.
Будем считать, что несжимаемая жидкость притекает к гидродинамически совершенной скважине радиусом r 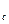 , расположенной в центре однородного горизонтального кругового пласта постоянной толщины h. На внешней круговой границе пласта радиусом r
, расположенной в центре однородного горизонтального кругового пласта постоянной толщины h. На внешней круговой границе пласта радиусом r 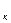 , служащей контуром питания, поддерживается постоянное давление Р
, служащей контуром питания, поддерживается постоянное давление Р 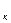 , на забое скважине давление Р
, на забое скважине давление Р 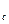 , тоже постоянно.
, тоже постоянно.
Дифференциальное уравнение в этом случае имеет вид:
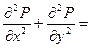 0 (14)
0 (14)
Введя замену r= 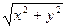 после соответствующих преобразований из (14) получим:
после соответствующих преобразований из (14) получим:
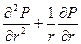 = 0 или
= 0 или 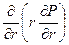 = 0 (15)
= 0 (15)
Уравнение (15) будем решать при следующих граничных условиях:
P=P 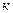 при r = rк ;
при r = rк ;
P=P 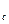 при r = r
при r = r 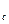 (16)
(16)
Дважды интегрируя (15) и учитывая (16), найдем закон распределения давления
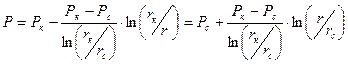 (17)
(17)
Скорость фильтрации 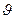 =
=  (18)
(18)
Дебит скважины  , где
, где 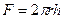 - поверхность, через которую происходит фильтрация с учетом (18) будем иметь
- поверхность, через которую происходит фильтрация с учетом (18) будем иметь
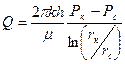 (19)
(19)
Формула (19) называется формулой Дюпюи.
Отношение дебита скважины Q к перепаду давления ∆Р называется коэффициентом продуктивности скважины (К). Из (19)
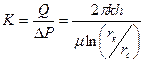 (20)
(20)
Закон движения частицы жидкости найдем из формулы 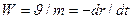
или 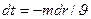 (21)
(21)
Подставив (18) в (21) и производя интегрирование в пределах от 0 до t и от r 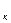 до r, получим
до r, получим 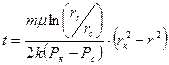 (22)
(22)
Время Т полного отбора жидкости из пласта определяется из (22) подстановкой r = r 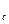 , т. е.
, т. е. 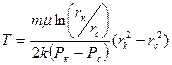 (23)
(23)
Средневзвешенное по объему порового пространства пластовое давление определяется из соотношения
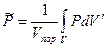 (24)
(24)
где V  =
= 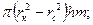
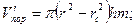
 (25)
(25)

Подставляя (17) и (25) в (24) и интегрируя полученное выражение в пределах от r 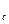 до r
до r 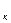 , получим
, получим
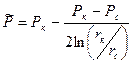 (26)
(26)
В (26) принято, что r 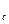 <<r
<<r 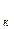 , т. е. r
, т. е. r 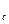
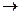 0 .
0 .
4. Расчет основных гидродинамических характеристик радиально-сферического фильтрационного потока.
Будем считать, что несжимаемая жидкость притекает к скважине, вскрывшей кровлю однородного пласта весьма большой толщины. Выделим на достаточно удаленной от забоя скважине полусферическую границу радиусом r 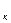 , на котором сохраняется постоянное давление Р
, на котором сохраняется постоянное давление Р 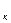 . На забое скважины радиуса r
. На забое скважины радиуса r 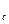 , поддерживается постоянное давление Р
, поддерживается постоянное давление Р  .
.
Дифференциальное уравнение установившейся фильтрации для рассматриваемого потока
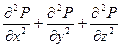 =0, (27)
=0, (27)
которое после замены r = 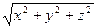 принимает вид:
принимает вид:
 0 или
0 или 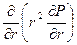 =0 (28)
=0 (28)
Уравнение (28) решаем при условиях:
P=P 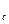 при r=r
при r=r 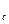
P=P 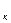 при r=r
при r=r 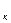 (29)
(29)
Решая уравнение (28) при условиях (29), найдем
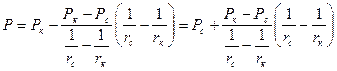 (30)
(30)
Далее
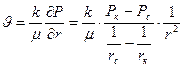 (31)
(31)
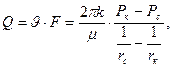 где
где 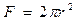 (32)
(32)
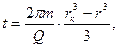
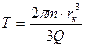 (33)
(33)
 (34)
(34)
Основная литература: 2 [51-68]
Дополнительная литература: 4 [51-65]
Контрольные вопросы:
1. Установившаяся фильтрация.
2. Простейшие фильтрационные потоки.
3. Средневзвешенное по объему пластовое давление.
4. Формула Дюпюи.
5. Индикаторная диаграмма.
6. Закон движения частицы.
7. Коэффициент продуктивности скважины.
Дата добавления: 2016-03-10; просмотров: 1589;
