Лекции № 11, 12. Интерференция скважин

Явление интерференции (взаимодействия) скважин заключается в том, что под влиянием пуска, остановки или изменения режима работы одной группы скважин изменяются дебиты и забойные давления другой группы скважин, эксплуатирующих тот же пласт. Вновь вводимые скважины взаимодействуют с существующими. Это явление взаимодействия и взаимовлияния скважин называется интерференцией.

Назовем точечным стоком (источником) на плоскости точку, поглощающую (выделяющую) жидкость. Сток (источник) можно рассматривать как центр добывающей (нагнетательной) скважины.

Введем потенциал Ф точечного стока, определяемый по формуле:

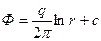(1)

где q=Q/h – дебит скважины-стока, приходящейся на единицу толщины пласта;

r – расстояние от стока до точки пласта, в которой определяется потенциал;

c – постоянное число.

Для точечного источника в формуле (1) дебит q считается отрицательным.

При совместном действии в пласте нескольких стоков (источников) потенциал Ф определяется для каждого стока (источника) по формуле (1). Потенциал, обуславливаемый всеми стоками и источниками, вычисляется путем сложения этих независимых друг от друга значений потенциалов, т. е. 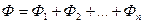или

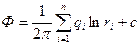(2)

где .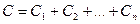

1. Приток жидкости в группе скважин в пласте с удаленным контуром питания (КП).

Пусть в горизонтальном пласте толщиной h расположена группа скважин 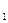А , А , … А 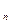радиусами r 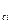, работающих с различными забойными потенциалами , где i = 1,2,…n.

Расстояние между центрами i – ой j – ой скважин известны ( 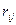= 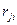). Так как контур питания (КП) находится далеко от скважин, то можно приближенно считать, что расстояние от всех скважин до всех точек КП одно и то же и равно r 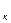. Потенциал Ф на КП считается заданным.

Потенциал в любой точке пласта М определяется по формуле (2). Потенциал на забое i – й скважины

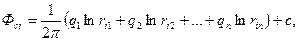(3)

где i = 1,2, … n.

Система (3) состоит n уравнений и содержит (n+1) неизвестных (n дебитов и постоянную интегрирования С). Дополнительное уравнение получим, поместив точку М на контур питания.

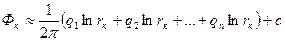(4)

Вычитая численно каждое из уравнений (3) из (4), исключим, постоянную C и получим систему из n уравнений, решив которую, можно определить дебиты скважин q если заданы забойные и контурный 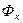потенциалы.

2. Приток жидкости к скважине в пласте с прямолинейным контуром питания (КП)

Пусть в полубесконечном пласте с прямолинейным КП, на котором потенциал равен 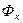, работает одна добывающая скважина с забойным потенциалом 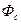. Необходимо найти q.

Для решения задачи зеркально отображаем скважину-сток относительно КП и дебиту скважины – отображению (источник) припишем знак минус.

Потенциал в любой точке пласта М:

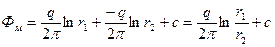(5)

Помещая последовательно точку М на стенку скважины (сток) радиуса r 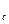и наКП, найдем

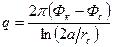(6)

где a – кратчайшее расстояние от скважины стока до КП.

3. Приток жидкости к скважине, эксцентрично расположенной в круговом пласте.

Пусть в плоском пласте постоянной толщины h с круговым КП радиуса r , на котором поддерживается постоянный потенциал 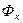, на расстоянии a от центра круга расположена скважина – сток 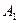с постоянным потенциалом .

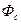Отобразим скважину-сток 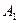фиктивной скважиной-источником 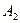относительно КП.

Потенциал в точке М пласта определяем по формуле (5). Помещая точку М на стенку скважины 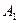и КП, определяем потенциалы 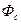и 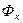, после чего находим

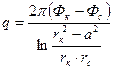(7)

4. Взаимодействие скважин кольцевой батареи

Рассмотрим совместное действие в пласте большой протяженности добывающих скважин, центры которых помещаются так, что скважины-стоки образуют кольцевую батарею радиуса a ( a< ).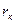

На КП радиуса 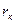потенциал 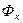, на стенке всех скважин – .

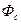По формуле (2) потенциал в точке М:

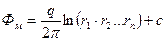(8)

Помещая точку М поочередно на КП и стенку скважины-стока и пренебрегая значением a по сравнению с 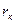, найдем дебит скважины:

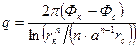(9)

Формула (9) приближенная.

Если величиной a по сравнению с 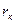, пренебречь нельзя, то необходимо пользоваться более точной формулой:

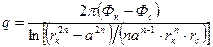(10)

Обозначим дебит скважины, определяемый по формулам (9) или (10) через , а дебит, определяемый по (7) через q.

Коэффициентом взаимодействия (интерференции) I, называют отношение дебита одиночно работающей скважины q к дебиту ее при совместной работе с группой скважин :

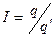(11)

Коэффициентом суммарного взаимодействия U, называют отношение суммарного дебита группы совместно работающих скважин, 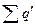к дебиту одиночно работающей скважины q:

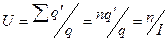(12)

Основная литература: 2 [52-96]

Дополнительная литература: 4 [125-155]

Контрольные вопросы:

1. Явление интерференции скважин.

2. Источники и стоки

3. Дебит скважины в пласте с прямолинейным контуром питания.

4. Дебит скважины эксцентрично размешенной на залежи.

5. Взаимодействие скважин кольцевой батареи.

6. Коэффициент взаимодействия скважин.

7. Коэффициент суммарного взаимодействия скважин.