Лекции № 14, 15, 16. Установившаяся фильтрация газа в пористой среде
Исследования показали, что хотя при установившейся фильтрации газа и происходит понижение температуры, оно относительно невелико даже при больших перепадах давления. Во многих случаях можно принимать для практических целей, что установившаяся фильтрация газа в пористых породах совершается в условиях изотермического изменения его состояния.
1. Дифференциальное уравнение установившейся фильтрации идеального газа.
Как было сказано ранее, для вывода дифференциального уравнения необходимо совместное решение уравнения неразрывности потока, уравнения движения и уравнения состояния.
Уравнение неразрывности потока:
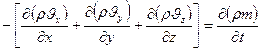 (1)
(1)
Уравнение движения:
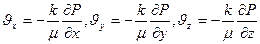 (2)
(2)
Уравнение состояния идеального газа:
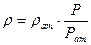 (3)
(3)
При установившейся фильтрации идеального газа
 = 0 (4)
= 0 (4)
С учетом (2) – (4) уравнение (1) принимает вид:
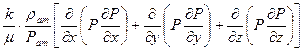 = 0
= 0
или 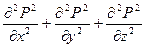 = 0 (5)
= 0 (5)
Сравнивая дифференциальное уравнение установившейся фильтрации идеального газа (5) с дифференциальным уравнением установившейся фильтрации несжимаемой жидкости, можно сделать вывод о аналогии, т. е. решения уравнения (5) должны быть аналогичны решениям дифференциального уравнения установившейся фильтрации несжимаемой жидкости. Только вместо Р необходимо брать 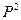 .
.
2. Прямолинейно-параллельный поток идеального газа.
Дифференциальное уравнение (5) в этом случае будет иметь вид:
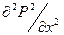 = 0 (6)
= 0 (6)
Примем граничные условия:
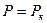 при x=0;
при x=0; 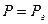 при x=L (7)
при x=L (7)
По аналогии с установившимся движением несжимаемой жидкости решение уравнения (6) при условиях (7) дает закон распределения давления в виде:
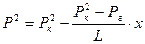
или 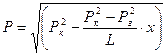 (8)
(8)
Скорость фильтрации:
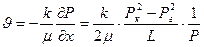 (9)
(9)
Дебит галереи, приведенный к атмосферному давлению
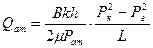 (10)
(10)
Средневзвешенное по объему пластовое давление
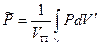 (11)
(11)
где 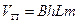 ,
,  ,
, 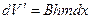 .
.
Тогда 
После интегрирования получим
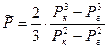 (12)
(12)
3. Плоскорадиальный фильтрационный поток идеального газа.
Дифференциальное уравнение (5) будет иметь вид:
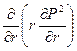 = 0 (13)
= 0 (13)
которое решается при следующих граничных условиях
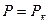 при
при 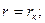
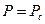 при
при 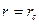 (14)
(14)
Решение уравнения (13) имеет вид:
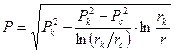 (15)
(15)
Уравнение (15) представляет собой закон распределения давления в пласте.
Скорость фильтрации
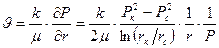 (16)
(16)
Дебит газовой скважины, приведенный к атмосферному давлению,
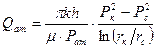 (17)
(17)
Средневзвешенное по объему пластовое давление определяется по (11) при 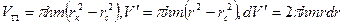 . После интегрирования (11) получим, пренебрегая величиной
. После интегрирования (11) получим, пренебрегая величиной  ,
,
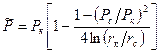 (18)
(18)
4. Плоскорадиальный фильтрационный поток реального газа по закону Дарси.
Если пластовое давление выше 10МПа и депрессия не слишком мала ( 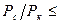 0,9), то уравнение состояния газа значительно отличается от уравнения состояния идеального газа и плотность газа определяется по формуле:
0,9), то уравнение состояния газа значительно отличается от уравнения состояния идеального газа и плотность газа определяется по формуле:
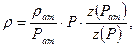 (19)
(19)
где z – коэффициент сверхсжимаемости газа. Кроме того, для высоких пластовых давлений нужно учитывать зависимость вязкости от давления
 (20)
(20)
или при малых изменениях давления
 (21)
(21)
где µ0 - вязкость при фиксированном давлении;
αµ - коэффициент, определяемый экспериментально и зависящий от состава газа.
Проницаемость пласта принимается постоянной.
Дебит газовой скважины, приведенный к атмосферному давлению,
 (22)
(22)
Имеется несколько способов вычисления интеграла в формуле (22), наиболее употребляем из которых следующий: по графикам зависимостей 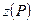 и
и  определяются значения
определяются значения 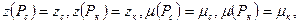 переменные
переменные 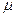 и z под знаком интеграла заменяются постоянными, равными
и z под знаком интеграла заменяются постоянными, равными 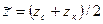 ,
, 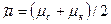 .
.
Тогда интеграл в формуле (22) вычисляется и (22) принимает следующий вид:
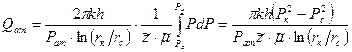 .
.
Основная литература: 2 [112-127]
Дополнительная литература: 4 [68-74]
Контрольные вопросы:
1. Какой газ называется идеальным?
2. Уравнения состояния идеального и реального газов.
3. Дифференциальное уравнение установившейся фильтрации идеального газа.
4. Закон распределения давления при фильтрации идеального газа.
5. Дебит газовой скважины.
6. Средневзвешенное по объему пластовое давление.
7. Коэффициент сверхжимаемости.
8. Зависимость вязкости реального газа от давления.
9. Дебит газовой скважины при фильтрации реального газа.
Дата добавления: 2016-03-10; просмотров: 2218;
