Лекция № 3. Закон Дарси – линейный закон фильтрации. Причины нарушения закона Дарси и пределы его применимости.

Подземная гидромеханика (ПГМ) – наука о движении (фильтрации) нефти, воды, газа и их смесей в пористых и трещиноватых горных породах, слагающих продуктивные пласты и массивы.

Так как ПГМ изучает разновидность механического движения, то её можно считать отделом механики.

Те или иные положения ПГМ устанавливаются и развиваются строгими или упрошенными математическими методами на основе данных о движении жидкости и газа в реальных пластах.

Существуют естественные подземные потоки пластовой жидкости. Движение жидкости и газа в пластах возникают каждый раз, когда начинают добывать из залежи нефти и газ. Это движение обладает специфическими особенностями, отличающими его от движения жидкости и газа по трубам и по открытым руслам. Знать особенности движения их движения в пористой и трещиноватой среде необходимо для того, чтобы вести успешную разработку нефтяных и газовых месторождений.

ПГМ – наука, применяемая не только для решения вопросов рациональной, разработки нефтяных и газовых месторождений. Гидротехнические сооружения (плотины, каналы, шлюзы, водоспуски и др.) проектируют на основе законов движения воды в грунтах. Законы ПГМ лежат в основе расчетов, относящихся к водоснабжению, ирригация, подземной газификации угля и др.

Чтобы успешно решать задачи ПГМ необходимо знание математики, физики, геологии, физики пласта, жидкости и газа и др. наук.

Начало развития ПГМ было положено в середине XIX столетия трудами французского инженера А.Дарси как и всякая наука ПГМ прошла до настоящего времени определенные этапы развития.

Основная литература: 2 [3-5]

Дополнительная литература: 4 [5-13]

Контрольные вопросы:

1. Что понимается под подземной гидромеханикой?

2. Кто считается основоположником подземной гидромеханики?

3. Этапы развития подземной гидромеханики.

Лекция № 2. Основные понятия подземной гидромеханики.

Под пористой средой подразумевается множества твердых частиц, тесно прилегающих друг другу, сцементированных или несцементированных, пространство между которыми (поры, трещины) может быть заполнено жидкостью и газом.

Фильтрацией называют движение жидкостей, газов и их смесей через твердые тела (вообще говоря, деформируемые) связанные между собой порами или трещинами.

Чрезвычайно малые размеры поровых каналов (единицы и десятки микрометров), их неправильная форма, большая поверхность шероховатых стенок все это создает огромные сопротивления движению жидкости и газа. Эти сопротивления служат главной причиной очень низкой скорости перемещения жидкости и газа в пористой среде.

Если объем пространства, занятого порами, не изменяется так, что его изменениями можно пренебречь, то пористая среда считается недеформируемой. Если же под влиянием упругих сил происходят такие изменения объема порового или трещиноватого пространства, величиной которых пренебрегать нельзя, то среду следует рассматривать как упругую (деформируемую).

В виду того, что поровые каналы имеют неправильную форму и самые разнообразные размеры, невозможно исследовать движение частиц жидкости или газа по всему множеству каналов. С самого начала развития теории фильтрации пошли по пути построения упрощенных моделей реальной пористой среды, называемых идеальными и фиктивными грунтами. Под идеальным грунтом понимается модель пористой среды, поровые каналы которой представляют собой пучок тонких цилиндрических трубок (капилляров) с параллельными осями. Фиктивным грунтом называется модель пористой среды, состоящая из шаров одинакового диаметра.

Одним из важных параметров, характеризующих пористую среду является пористость, измеряемая коэффициентом пористости (m), равного отношению объема пор V_п в некотором элементе пористой среды ко всему объему V данного элемента. Другим параметром пористой среды служит просветность (площадная пористость), измеряемая коэффициентом просветности n, равная отношению площади просветности F_п в некотором сечении пористой среды ко всей площади этого сечения F.

Средняя просветность по пласту 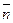равна пористости ( 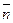=m).

Рассмотрим величину, называемую скоростью фильтрации 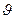, под которой понимается объемный расход жидкости (газа) в единицу времени Q через единицу площади поперечного сечения F, т.е.

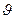=∆Q/∆F (1)

Так как расход (∆Q) делится на полную площадь (∆F), а не на ее часть, занятую порами, то очевидно, что скорость фильтрации 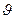не является действительной средней скоростью движения W в живом сечении фильтрационного потока. Учитывая, что 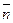=m, будем иметь:

W= 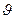/m (2)

Основная литература: 2 [6-9]

Дополнительная литература: 4 [14-20]

Контрольные вопросы:

1. Что понимается под фильтрацией?

2. Коэффициент пористости.

3. Коэффициент просветности.

4. Скорость фильтрации.

Лекция № 3. Закон Дарси – линейный закон фильтрации. Причины нарушения закона Дарси и пределы его применимости.

В середине ХIХ века в результате экспериментального изучения движения воды через песчаные фильтры был установлен закон Дарси – основной закон фильтрации или линейный закон фильтрации. В результате тщательно проведенного эксперимента Анри Дарси получил формулу

Q=kф·F·∆H/L (1)

где Q – объемный расход жидкости через песчаный фильтр, длина которого L, а площадь поперечного сечения F, ∆H=H1-H2 – разность напоров воды над фильтром и у его основания; kф – коэффициент фильтрации, который зависит от структуры пористой среды и от свойств фильтрующейся жидкости.

Коэффициент фильтрации kф используется обычно в гидромеханических расчетах, где приходится иметь дело с одной жидкостью – водой. При исследовании фильтрации нефти, газа и их смесей необходимо разделить влияние свойств пористой среды и жидкости. В этом случае формула Дарси имеет вид

Q= 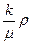g F (2)

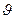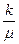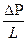или = · (3)

где, μ – динамический коэффициент вязкости, Па с;

P=ρgh, гидростатическое давление, Па;

k - коэффициент проницаемости, .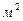

Проницаемость – способность породы пропускать через себя жидкость, газ или их смеси под воздействием приложенного перепада давления.

Сравнивая (1) и (2), получим:

K_ф = kρg/μ (4)

Формула (3) носит название линейного закона Дарси.

В процессе исследования пределов применимости закона Дарси показано, что существуют две основные группы причин отклонения от закона Дарси:

1) отклонения, связанные с проявлением инерционных сил при высоких скоростях фильтрации (верхняя граница применимости закона Дарси);

2) отклонения при достаточно малых скоростях фильтрации с проявлением неньютоновских реологических свойств жидкости, ее взаимодействием с твердым скелетом пористой среды (нижняя граница применимости закона Дарси).

Верхнюю границу применения закона Дарси связывают обычно с некоторым критическим (предельным) значением числа Рейнольдса (Reкр):

Reкр= 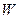d/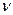

где, d – некоторый характерный размер пористой среды;

W – средняя скорость течения по трубам;

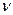- кинематический коэффициент вязкости флюида ( 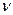= 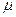/ρ).

Удобную для практики разработки нефтяных и газовых месторождений формулу числа Re предложил В. Н. Щелкачев:

Re= 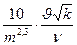(5)

По В. Н. Щелкачеву критические значения Re, заключены в интервале:

Reкр=0,032÷14.

Нижняя граница применимости закона Дарси связана с проявлением неньютоновских свойств фильтрующихся флюидов, что характеризуется повышенным содержанием в нефти высокомолекулярных компонентов (смол, асфальтенов, парафина и др.). В этом случае предлагается нелинейный закон фильтрации неньютоновских жидкостей, в основе которого лежит модель фильтрации с предельным градиентом, в виде:

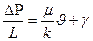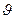, >0,

(6)

где γ – предельный (начальный) градиент давления, по достижении которого начинается движение жидкости; при меньших значениях градиента движение отсутствует.

Основная литература: 2 [9-22]

Дополнительная литература: 4 [20-33]

Контрольные вопросы:

1. Что понимается под проницаемостью пласта?

2. Линейный закон Дарси.

3. Число Рейнольдса.