Формальное описание понятий предметной области (ПО)

Знак – это заменитель некоторого предмета, явления или события, используемый для накопления, хранения, переработки и передачи информации.

Объем понятия - это множество (класс) всех сущностей, обладающих существенными признаками понятия.

Содержание понятия - совокупность всех существенных признаков (свойств) данного понятия, которые позволяют однозначно идентифицировать данное понятие. Другими словами, объем понятия включает все предметы и объекты ПО, которые могут быть описаны данным понятием.

Имя понятия - это символьное обозначение понятия, играющее роль ссылки.

Денотат понятия - это пара, состоящая из имени и знака, обозначающая сущность ПО, при этом отдельно выделяют понятия - денотат знака и денотат имени. Денотат знака - это значение, которое может иметь в рамках данной знаковой ситуации. Следует иметь в виду, что связь "имя-денотат" многозначна. Некоторое имя может обозначать множество денотатов - омонимия, и наоборот, одному денотату можно поставить несколько имен - синонимия.

Признаки понятия подразделяются на три типа:

- дифференциальные - используются в качестве характеристики содержания понятия;

- характеристические - это признаки, позволяющий отличать сущности, относящиеся к объему одного и того же понятия;

- валентные - это признаки, обеспечивающие связь между различными понятиями. Без потери общности можно считать такие связи бинарными.

Признак характеризуется именем и значением. Обычно выделяют следующие типы значений признаков: логические, числовые, символьные и др. Имя признака позволяет указать ту семантическую роль, которую играет его значение в организации связи между сущностью и признаком, её характеризующим.

Схема понятия – совокупность имен дифференциальных, характеристических и валентных признаков составляет схему понятия, обозначаемую как shm P. Тогда

shm P = <D, H, V>,

D = {D_i | i=1, .... n} - множество имен дифференциальных признаков;

Н = {h_j | j=1, ..., т} - множество имен характеристических признаков;

V= {V_k | k=1, .... l} - множество имен валентных признаков;

D={d_i | i=1,...,n}.

Пара (A_i, aⁱ_j) обозначает, что признак с именем A_i может принимать значение aⁱ_j, при этом аⁱ_j Î domA_i. Здесь domA_i обозначает множество – домен всех возможных значений признака А_i.

Тогда каждая сущность может быть представлена тройкой пар:

е = {(D_i, dⁱ_n), (Н_j, h^j_m), (V_k,v^k_l)}.

Более подходящей формой представления понятия является логическая формула.

Логические формулы понятий.

Любое понятие может быть представлено формулой:

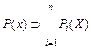(1)

P_i(X) - предикаты, которые могут интерпретироваться как другие понятия или как признаки понятия Р(Х).

Если учесть классификацию признаков, то формулу можно представить в виде:

(2)

Устанавливая различные значения дифференциальных признаков, можно получить класс понятий с однородной структурой, т.е. все понятия обладающие одинаковой схемой.

Формуле (1) эквивалентна запись

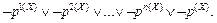(3)

Эта форма записи называется хорновским дизъюнктом, т.е. дизъюнкт который содержит не более одного позитивного элемента.

Концепт понятия - включает в себя как собственные признаки, идентифицирующие понятие, так и признаки, позволяющие установить связь данного понятия с другими (валентные признаки). Если понятие является сложным, то в концепт могут входить правила, необходимые и достаточные для принятия решения о принадлежности данной сущности объему понятия. Другими словами концепт - это то знание, которое выражается данным понятием при концептуальном моделировании предметной области.

Категории денотат и концепт используются в семиотике, в логике их аналогами являются термины "экстенсионал" и "интенсионал"'.

Множество всех объектов, предметов или сущностей, являющихся денотатами понятия, составляет объем, или экстенсионал понятия. Будем обозначать экстенсионал через extP,

ext P={e₁, e₂, ..., e_n},

где e₁, е₂,.... е_n - сущности, являющиеся денотатами понятия Р.

Экстенсионал понятия - это совокупность всех его допустимых денотатов, соответствующих концепту этого понятия.

Если понятие имеет одно значение некоторого признака, то между экстенсионал понятия и его признаками может быть установлена функциональная связь вида /₁: extP ® domA_i.

Эта функциональная связь сопоставляет любые сущности eⁱ_j Î extP некоторое значение признака zⁱ_j Î domA_i.. Разные понятия могут иметь один и тот же экстенсионал, но выражать разный смысл.

Интенсионал понятия - это тот смысл, который мы вкладываем в понятие, т.е. интенсионал характеризует концепт данного понятия, его содержание (intP).

Существует два подхода к формальному описанию интенсионала: теоретико-множественный и логический. При теоретико-множественной формализации в интенсионал обычно включают множество всех дифференциальных признаков, характеризующих понятие:

int_SPs={(D₁, d¹), (D₂, d²), .... (D_n, dⁿ)},

где D_i – имя дифференциального признака, a dⁱ – соответственно его значение, (D₁, d¹), (D₂, d²), .... (D_n, dⁿ) – совокупность дифференциальных признаков, индекс 5 идентифицирует теоретико-множественную формализацию.

Этот подход игнорирует имена характеристических и валентных признаков, т.е. в нем не заложена схема понятия, наличие которой удобно использовать для принятия решения о принадлежности некоторой сущности экстенсионалу данного понятия (необходимое и достаточное условия). Поэтому для сложных понятий используется логическая форма (хорновские дизъюнкты)представления интенсионала. Под интенсионалом понятия будем понимать правую часть импликации (1), т.е. 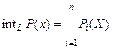(4)

Соответственно если понятие представлено логической формулой (2), то интенсионал может быть определен выражением

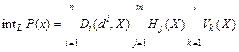(5)

Логическая формула допускает следующую интерпретацию: интенсионал понятия Р принимает истинное значение на всех сущностях е_i Î extP.

Суммируя вышеизложенное, можно представить понятие в виде

P=<intP, extP, shmP> (7)

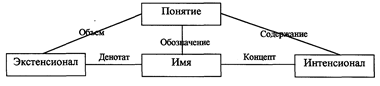
Связь между различными категориями, используемыми в логике и семиотике для описания понятия следующая