Облическое преобразование факторных решений
6.24 Практика научных исследований показывает, что очень часто группы антропологических признаков, выделяемые факторным анализом, оказываются скоррелированными друг с другом. Вследствие этого при проведении ортогональной ротации факторных осей бывает невозможно так провести эти оси, чтобы они одновременно проходили бы через центры точек, представляющих признаки (рис.6.10). Это приводит к тому, что те нагрузки, которые в соответствии с принципом простой структуры должны были бы быть практически нулевыми, оказываются все еще далекими от нуля. Вместе с тем, если пренебречь условием ортогональности факторов, которое значительно упрощает применение факторного анализа, но не всегда соответствует реальной ситуации, и осуществлять переход к облическим осям, то каждая из новых координат может быть достаточно точно проведена через центр группы конечных точек векторов, представляющих исходные признаки (рис.6.10). Угол между косоугольными осями a определит их коэффициент корреляции r = arccos a. Если ортогональная ротация, например, системы двух факторов заключалась в повороте координат на некоторый угол j, то облическое преобразование предполагает поворот первого косоугольного фактора u1 на угол f1 и аналогичное вращение второй оси u2 на угол f2.
- 144 -
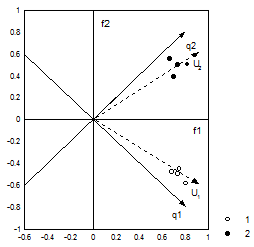
Рисунок 6.10. Принцип вращения исходных факторных осей f1 и f2 к новым ортогональным q1 и q2 и облическим u1 и u2 факторным осям. Обозначения: 1 и 2 – признаки из двух разных групп
При работе с ортогонально преобразованными факторами требовалось анализиро-вать одну матрицу факторного отображения A2, элементы которой одновременно явля-лись коэффициентами корреляции факторов с признаками. Использование облических осей резко увеличивает количество результатов факторного анализа, так как в этой ситуации приходится рассматривать три матрицы: отображения - A, структуры - Rf и корреляций между факторами - Ф. Теперь элементы матрицы A перестают быть коэффициентами корреляциями признаков с факторами или нагрузками. Эти коэффициенты теперь содержит матрица Rf. Между тремя матрицами результатов облического факторного решения существуют простые соотношения: Rf = AФ и A = Rf Ф-1.
На самом деле усложнение результатов факторного анализа в облических осях оказы-вается еще большим. Дело в том, что часто бывает так, что для матрицы факторного отображения A может наблюдаться простой вид, тогда как для матрицы факторной струк-туры Rf этого не будет (рис.6.11). Пусть имеется некоторый признак, конечная точка век-тора которого располагается вблизи облического фактора u1. Тогда в соответствии с принципами работы в косоугольной системе координат его элемент факторного отображения на фактор u1 может быть получен как проекция, образованная линией, проведенной параллельно другой оси u2. Аналогично, элемент отображения признака на ось u2 может быть найден как проекция на нее, полученная при помощи линии, параллельной оси u1. Нетрудно видеть, что элемент отображения признака на фактор u1 - велик, а для оси u2 - мал, что соответствует желаемой простоте описания.
Однако, значения коэффициентов корреляции (нагрузки) признака с факторами u1 и u2 находятся по иным геометрическим принципам. Для их определения требуется из точки конца вектора-признака опустить перпендикуляры на эти оси. На рисунке 6.11 видно, что корреляция признака с фактором u1 имеет большую величину, но можно также найти, что аналогичная корреляция с осью u2 весьма далека от желательного для нас нулевого уровня.
- 145 -
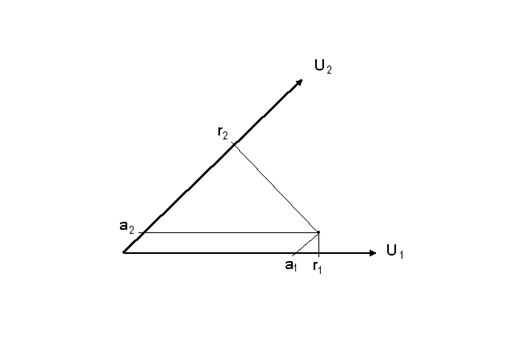
Рисунок 6.11. Определение элементов отображения aij и нагрузок rij на облические факторы u1 и u2
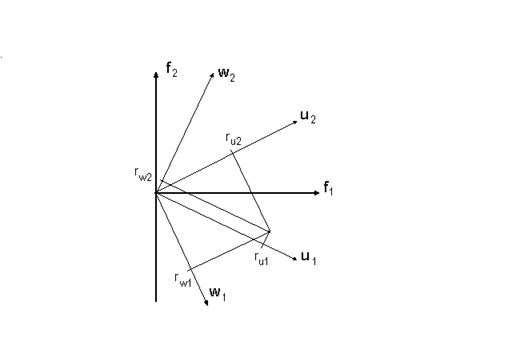
Рисунок 6.12. Облическая ротация с использованием первичных u1 и u2 и вторичных w1 и w2 факторов. Показаны нагрузки некоторого признака на эти факторы - ru1, ru2, rw1, rw2
- 146 -
Таким образом, применение облической ротации в стремлении к наиболее полному достижению простого вида одной из матриц - факторного отображения A , часто приводит к тому, что исследователь получает еще одну матрицу - факторной структуры Rf, которая может включать только достаточно высокие по величине коэффициенты корреляции.
6.25 Парадоксальность облической ротации может быть устранена введением дополнительной системы факторных осей. Для простейшего примера двух факторов это может быть наглядно изображено графически (рис.6.12). Пусть при помощи облической ротации были введены факторы u1 и u2, которые можно назвать первичными осями. Пусть для них факторное отображение имеет простой вид, а факторная структура его не имеет. Введем новую факторную ось w2 так, чтобы она была бы перпендикулярной первичной координате u1. Аналогично, введем новую ось w1 перпендикулярную u2. Оси u1 и u2 называются первичными, а w1 и w2 - вторичными облическими факторными координатами. Смысл введения вторичной облической системы координат заключается в следующем.
Для некоторого признака величина элемента факторного отображения на ось u2 - мала (рис.6.12), а коэффициент его корреляции с фактором u2 - довольно далек от нуля. Нетрудно видеть, что аналогичная связь с вторичной факторной осью w2 будет столь же малой, что и нагрузка на u2, что является желательным. Таким образом, если матрица факторной структуры для первичных осей Rf uбыла далеко не простого вида, то для аналогичной матрицы структуры у вторичных факторов Rf w такая простота может быть достигнута.
Таким образом, при работе с системами первичных (u1 и u2 ) и вторичных (w1 и w2 ) факторных осей мы получим шесть матриц. Для факторов u1 и u2 будут свойственны: матрица факторного отображения Au , матрица факторной структуры Rf u , матрица коэффициентов корреляции между факторами Фu. Для факторов w1 и w2 можно получить аналогичные матрицы Aw , Rf w и Фw. Из этих шести результатов простым видом будут отличаться только матрица отображения первичных факторов Au и матрица структуры вторичных факторов Rf w. В соответствии с принципами косоугольной ротации эти две матрицы и должны интерпретироваться. Наибольший интерес представляет матрица Rf w, так как именно в ней содержатся коэффициенты корреляции вторичных факторов и исходных признаков.
6.26 Общие принципы облической ротации факторных осей принципиально сходны с ортогональным вращением, хотя оказываются заметно более сложными. В ортогональном случае новая матрица факторного отображения для простейшего случая двух факторов A2 в соответствии с принципами аналитической геометрии находилась по формуле A2 = A1T, где элементы матрицы трансформации T определялись углом поворота системы факторных осей f

 cos j -sin j
cos j -sin j
T =
sin j cos j
Облическая ротация к системе первичных факторов осуществляется аналогичным образом. Так, матрицу первичной факторной структуры можно получить из равенства
- 147 -
Rf u = ATu, (6.56)
где A- отображение ортогональных факторов, а трансформационная матрица Tu находится в виде

 cos j1 cos j2
cos j1 cos j2
Tu = , (6.57)
sin j1 sin j2
при j1 - угле поворота фактора u1 и j2 - аналогичном значении для u2. Эти углы отсчитываются от одной из ортогональных факторных осей.
Корреляционная матрица первичных факторов Фu может быть найдена по формуле
Фu = Tu' Tu , (6.58)
а матрица факторного отображения - получена по стандартному равенству
Au = Rf uФu-1 . (6.59)
Для перехода к вторичным косоугольным факторам w1 и w2 следует найти трансформационную матрицу Tw, для чего применима формула
Tw = TuФu-1D , (6.60)
где D - диагональная матрица, включающая значения коэффициентов корреляции между факторными осями u1 и w1, u2 и w2. Корреляции осей u1 и w2, u2 и w1 равны нулю, что следует из принципа их взаимной перпендикулярности. Тогда для системы вторичных факторов w1 и w2 можно получить матрицу факторного отображения
Aw= ATw , (6.61)
где A- отображение ортогональных факторов. Корреляционная матрица вторичных факторов равна
Фw = Tw' Tw , (6.62)
и факторная структура может быть найдена по формуле
Rfw = AwФw-1 . (6.63)
Кроме этого, определенные соотношения существуют и между результатами факторных решений для первичных (u1 и u2) и вторичных (w1 и w2) облических осей. Так, имею-щие простой вид первичная матрица отображения Auи вторичная матрица структуры Rf w связаны формулой
Rf w = AuD , (6.64)
где D - диагональная матрица, включающая значения коэффициентов корреляции между факторными осями u1 и w1, u2 и w2. Аналогично, можно выписать также соотношение вторичной матрицы отображения Aw и первичной матрицы структуры Rf u
Rf u = AwD . (6.65)
Вид трансформационных матриц Tu и Tw, зависящих только от углов поворота двух осей j1 и j2, остается таким лишь для простейшего случая двух факторов. При работе с большим числом косоугольных осей ситуация усложняется. С подробностями применения формул (6.56) - (6.65) можно познакомиться в книге Г.Хармана (1972).
6.27 Очевидно, что облическая ротация факторных осей определяется в конечном счете значениями их углов поворота. Нахождение их конкретных величин может быть осуществлено несколькими способами, из которых в настоящее время обычно применяются аналитические. Вместе с тем, существуют способы облического преобразования факторных осей, предполагающие значительное диалоговое участие исследователя в этой про-
- 148 -
цедуре, причем его субъективные решения имеют основное значение и в большой степени определяют конечный результат.
Использование аналитических методов облического преобразования основано на тех же самых логических посылках, на которых базируются приемы ортогональной ротации. Здесь также конструируются специальные критерии, которые должны принимать свои экстремальные значения в случаях, когда достигается необходимая простота структуры одной из матриц, являющихся искомым результатом облической ротации.
Правда, количество таких критериев оптимальности косоугольного преобразования довольно велико и среди них трудно выбрать наилучший. Эта ситуация резко отличается от той, которая сложилась для ортогональной ротации, где метод варимакс как правило считается стандартным и дающим обычно наилучшие результаты.
Как мы видели, целью облической ротации является получение матрицы вторичной факторной структуры

 r1w1 r1w2 r1w3 ... r1wn
r1w1 r1w2 r1w3 ... r1wn
r2w1 r2w2 r2w3 ... r2wn
Rf w = r2w1 r2w2 r2w3 ... r2wn ,
... ... ... ... ...
rmw1 rmw2 rmw3 ... rmwn
где ri w j - корреляция i-го признака с j-м вторичным фактором wj. Очевидно, эта матрица должна содержать как можно больше крупных по абсолютной величине или близких к нулю коэффициентов корреляции.
Одним из возможных критериев простоты матрицы вторичной факторной структуры может служить выражение
m n
S S ri w j4
i = 1 j = 1
 K = . (6.66)
K = . (6.66)

 m n 2
m n 2
S S ri w j2
i = 1 j = 1
Формула K основана на тех же самых соображениях, что и критерий квартимакс (6.49), предназначенный для ортогональной ротации. В ситуации, когда матрица Rfw будет включать большое количество крупных элементов, близких по абсолютной величине к 1, их общая сумма четвертых степеней, найденная по всей матрице, будет иметь заметно большее значение, чем в случае, когда Rf w окажется заполненной средними по величине элементами. Знаменатель формулы позволяет осуществлять нормировку этой суммы. Итак, условием простоты матрицы Rf w может быть достижение наибольшего значения K, т.е. K = max , что приводит к так называемому облимакс подходу Саундерса. По существу здесь представлена облическая аналогия ортогонального метода квартимакс-ротации.
Другой подобный критерий может быть основан на сумме вида
m n
N = S S ri w j2 ri w k2 . (6.67)
i = 1 k > j=1
- 149 -
Здесь для каждого исходного i-го признака получается сумма всех попарных произведений квадратов его коэффициентов корреляции со всеми вторичными факторами, т.е. - ri w12 ri w22 + ri w12 r iw32 + ri w12 ri w42 + ... и т.д. Затем эти суммы складываются для всех m признаков. Эта формула основана на тех же соображениях, что и критерий (6.50), предназначенный для ортогональной ротации. Если матрица Rf w будет содержать большое количество близких к нулю элементов, то значительная часть произведений ri wj2 ri wk2 также будет очень близкой к нулю, а их общая сумма N будет иметь малую величину. Таким образом, одним из условий простоты вида матрицы вторичной факторной структуры сможет являться достижение минимальной величины критерия (6.74) N = min, что приводит к так называемому методу квартимин Кэррола для облической ротации.
При проведении ортогонального вращения максимизация критерия (6.49) и минимизация выражения (6.50) давали один и тот же результат и приводили к единому методу квартимакс-ротации. В облическом случае их аналоги (6.66) и (6.67) не равноценны, и каждый из них приводит к своему методу косоугольного преобразования факторов (облимаксу или квартимину).
Третий подход к получению аналитического критерия облического вращения факторов привел к целому семейству подходов, называемому облимин-методами Кэррола. Здесь были использованы соображения, сходные с теми, которые легли в основу варимакс-критерия ортогонального вращения. В тех случаях, когда матрица Rfw будет содержать много близких к нулю элементов, ковариация квадратов этих элементов

 n m m m
n m m m
C = S m S ri wj2 ri wk2 - S ri wj2 S riwk2 (6.68)
k>j=1 i = 1 i = 1 i = 1
будет иметь иметь минимальную величину. Достижение минимального значения этого критерия называется коваримин методом облической ротации. Позже, на основе этого критерия была получена другая более общая формула облимин-критерия

 n m m m
n m m m
В = S m S ri wj2 ri wk2 - g S ri wj2 S riwk2 (6.69)
k>j=1 i = 1 i = 1 i = 1
где g некоторый параметр, который может принимать разные значения, давая сразу три способа облической ротации. Достижение минимума критерия B при g = 0 превращает его в формулу метода квартимин. Аналогично, при g = 1 наблюдается равенство B = C, что приводит к методу коваримин. Наконец, минимизация критерия B при g = 0.5 дает особый метод биквартимин. При практическом применении различных частных случаев облимин-критерия установлено, что метод квартимин склонен давать косоугольные факторы, связанные чрезмерно высокой корреляцией, тогда как коваримин-метод обычно дает систему осей, близкую к ортогональной. Биквартимин-критерий дает какое-то промежуточное решение.
Четвертый подход к построению критерия облической ротации привел к бинормамин-методу, основанному на формуле


 n m m m
n m m m
D = S S ri wj2 ri wk2 S ri wj2 S ri wk2 . (6.70)
k > j=1 i = 1 i = 1 i = 1
- 150 -
По своим свойствами этот критерий должен избегать крайностей квартимин- и коваримин-ротации.
В формулы (6.66) - (6.70) входят квадраты коэффициентов корреляции признаков со вторичными факторами ri wj2. Вместе с тем, так же как для случая ортогональной ротации, для устранения влияния различий величины общностей признаков, обычно вместо нагрузок в эти формулы входят нормированные на общности значения этих элементов матрицы вторичной факторной структуры
ri wj2
 vi w j = .
vi w j = .
hi2
С подробностями применения перечисленных критериев для проведения облической ротации можно познакомиться в книге Г.Хармана (1972). Эти вычислительные процедуры организованы по итерационному принципу, когда шаг за шагом получаются все более точные результаты. Вычисления завершаются, когда величина соответствующего критерия перестает сколько-нибудь значительно изменяться.
Все перечисленные выше аналитические подходы к облической ротации были ориентированы на получение простого вида для матрицы вторичной факторной структуры. Существует метод, который оптимизирует вид матрицы первичного факторного отображения, что позволяет избежать работы с системой вторичных факторов. Он называется прямым методом облимин. Его критерием служит функция

 n m d m m
n m d m m
 G = S S ai u j2 ai uk2 - S ai uj2 S ai uk2 , (6.71)
G = S S ai u j2 ai uk2 - S ai uj2 S ai uk2 , (6.71)
k > j=1 i = 1 m i = 1 i = 1
где параметр d может принимать различные значения. В этой формуле вместо коэффициентов корреляции признаков с вторичными факторами ri wj используются ai uj - элементы факторного отображения на первичные факторы. При d = 0 метод дает наиболее косоугольные оси. При отрицательных значениях d результаты облической ротации становятся все более близкими к ортогональному случаю.
Кроме перечисленных существуют и другие аналитические методы облической ротации факторов: максплейн, ортоблик, иерархический факторный анализ, подход с использованием целевой матрицы и др.
6.28 Из приведенного краткого обзора методов получения облической ротации можно видеть, что стремление максимально упростить факторное решение с применением косоугольных факторов может не приводить к однозначным результатам, вследствие существования большого количества подходов, дающих существенно неодинаковые факторные решения. Но даже при получении какого-то, удовлетворяющего интуицию исследователя, простого вида матрицы первичного факторного отображения Au или матрицы вторичной факторной структуры Rw это решение в целом оказывается все-таки громоздким, так как кроме них включает также матрицы коэффициентов корреляции первичных Фu и вторичных факторов Фw. В результате приходится интерпретировать все эти четыре матрицы. Таким образом, стремление к простоте некоторых результатов факторного анализа ведет к значительному их усложнению в целом.
- 151 -
Вместе с тем, при проведении только одного лишь ортогонального преобразования исследователь имеет дело всего лишь с единой матрицей A. К тому же, во многих случаях облические факторы обнаруживают не слишком высокие взаимные корреляции и получающаяся система осей может считаться объективно близкой к ортогональной. Более того, использование некоторых методов косоугольной ротации (коваримин, прямой облимин с отрицательными значениями параметра d) обычно приводит к результатам с невысокими корреляциями факторных осей.
Поэтому, в отношении целесообразности применения облической ротации среди специалистов по факторному анализу единой точки зрения нет. Сторонники американ-ской школы Терстона-Кеттела считают косоугольное преобразование факторов необходимым и лучше соответствующим реальным закономерностям коррелированности признаков. Специалисты, принадлежащие к английской школы Барта, считают возможным ограничиваться применением только ортогональных факторов, так как это позволяет достигнуть большей компактности всего факторного решения в целом.
По-видимому, при достижении достаточно интерпретируемых результатов с применением ортогональной ротации в дополнительном облическом преобразовании особой необходимости нет. Однако, если смысл ортогональных факторов остается неясным, облическая ротация - неизбежна.
Таблица 6.8 Результаты облической ротации факторного решения для 20 размеров черепа
| Признаки | |||
| Косоугольное факторное отображение | |||
| 1.Продольный диаметр | 0.081 | 0.312 | 0.301 |
| 2.Поперечный диаметр | 0.738 | -0.151 | -0.074 |
| 3.Высота черепа от br | 0.093 | 0.070 | 0.149 |
| 4.Длина основания черепа | -0.024 | 0.289 | 0.130 |
| 5.Наименьший диаметр лба | 0.600 | 0.124 | 0.018 |
| 6.Наибольший диаметр лба | 0.675 | -0.207 | 0.016 |
| 7.Ширина основания черепа | 0.705 | -0.004 | -0.059 |
| 8.Ширина затылка | 0.458 | -0.043 | 0.138 |
| 9.Длина основания лица | -0.161 | 0.821 | 0.073 |
| 10.Верхняя ширина лица | 0.624 | 0.371 | 0.010 |
| 11.Биорбитальный диаметр | 0.565 | 0.272 | 0.082 |
| 12.Скуловой диаметр лица | 0.640 | 0.146 | 0.049 |
| 13.Средняя ширина лица | 0.310 | 0.415 | 0.090 |
| 14.Верхняя высота лица | -0.033 | 0.129 | 0.808 |
| 15.Ширина правой орбиты | 0.320 | 0.084 | 0.328 |
| 16.Высота правой орбиты | 0.076 | -0.206 | 0.542 |
| 17.Ширина носа | 0.201 | 0.465 | -0.196 |
| 18.Высота носа | -0.045 | 0.061 | 0.703 |
| 19.Длина неба | -0.114 | 0.642 | 0.108 |
| 20.Ширина неба | 0.140 | 0.500 | -0.165 |
- 152 -
Таблица 6.8 (Продолжение)
| Признаки | |||
| Косоугольная факторная структура | |||
| 1.Продольный диаметр | 0.231 | 0.395 | 0.381 |
| 2.Поперечный диаметр | 0.681 | 0.038 | 0.052 |
| 3.Высота черепа от br | 0.144 | 0.126 | 0.183 |
| 4.Длина основания черепа | 0.083 | 0.308 | 0.183 |
| 5.Наименьший диаметр лба | 0.638 | 0.293 | 0.170 |
| 6.Наибольший диаметр лба | 0.621 | -0.018 | 0.117 |
| 7.Ширина основания черепа | 0.691 | 0.178 | 0.089 |
| 8.Ширина затылка | 0.476 | 0.111 | 0.227 |
| 9.Длина основания лица | 0.081 | 0.791 | 0.205 |
| 10.Верхняя ширина лица | 0.728 | 0.545 | 0.217 |
| 11.Биорбитальный диаметр | 0.657 | 0.444 | 0.257 |
| 12.Скуловой диаметр лица | 0.690 | 0.332 | 0.214 |
| 13.Средняя ширина лица | 0.443 | 0.518 | 0.240 |
| 14.Верхняя высота лица | 0.173 | 0.283 | 0.827 |
| 15.Ширина правой орбиты | 0.412 | 0.239 | 0.412 |
| 16.Высота правой орбиты | 0.134 | -0.075 | 0.516 |
| 17.Ширина носа | 0.288 | 0.481 | -0.060 |
| 18.Высота носа | 0.121 | 0.191 | 0.706 |
| 19.Длина неба | 0.085 | 0.632 | 0.214 |
| 20.Ширина неба | 0.243 | 0.505 | -0.034 |
Пример 6.7 Проведем облическую ротацию по прямому методу облимин для результатов факторного анализа 20 размеров черепа, полученных в предыдущем примере 6.6. В связи с тем, что найденный после ортогонального вращения четвертый фактор описывал связи небольшой группы признаков (биорбитального диаметра, ширины орбиты и верхней ширины лица), косоугольному преобразованию подвергались только три факто- ра. При запуске процедуры прямой облической облимин-ротации задавалось значение параметра d = 0, что соответствует получению максимально косоугольного решения.
Рассмотрим матрицу косоугольного факторного отображения (табл.6.8). Первый фактор имеет высокие коэффициенты для поперечного диаметра и ширины основания черепа, а также - для наибольшего лобного диаметра. Несколько меньшие коэффициенты проявляются для наименьшего диаметра лба, скулового диаметра, верхней высоты лица и ширины затылка. Таким образом, этот фактор описывает поперечное развитие черепа, преимущественно - нейрокраниума.
Наибольшие коэффициенты факторного отображения для второго облического фактора наблюдаются у длины основания лица и размеров неба. Заметно меньшие значения этих коэффициентов на этот фактор можно найти для ширины носа и средней ширины лица.
- 153 -
Таблица 6.9 Матрица коэффициентов корреляции облических факторов для 20 размеров черепа
| Фактор | |||
| 1.000 | 0.276 | 0.212 | |
| 0.276 | 1.000 | 0.202 | |
| 0.212 | 0.202 | 1.000 |
Третий облический фактор описывает продольное развитие лица, имея наибольшие значения коэффициентов матрицы факторного отображения у верхней его высоты и высоты грушевидного отверстия. Несколько меньшая нагрузка наблюдается для высоты
орбиты.
При сопоставлении результатов облической ротации и варимакс-преобразования (табл.6.7) можно видеть принципиальное сходство. Для матрицы факторной структуры интерпретация облического факторного решения оказывается сходной с той, которую можно провести для факторного отображения. Однако, следует заметить, что для нагрузок наблюдается меньшая простота решения. Это проявляется в том, что большие и малые значения нагрузок у разных признаков на каждый фактор различаются не столь отчетливо как это характерно для элементов факторного отображения. Это - вполне естественный результат, так как метод прямой облимин-ротации ориентирован на упрощение именно матрицы факторного отображения, которая и должна здесь интерпретироваться.
Достоинством облических факторов является то, что можно получить представление о коррелированности соответствующих им закономерностей вариации групп признаков (табл.6.9). Можно видеть, что три основные закономерности связей размеров черепа, описываемые тремя косоугольными факторами, скоррелированы с теснотой 0.2 - 0.3, что примерно соответствует средним значениям корреляций между исходными признаками.
Дата добавления: 2016-02-13; просмотров: 1125;
