Метод главных факторов
6.12 Метод главных факторов логически сходен с методом главных компонент. Основным отличием является то, что главные компоненты основываются на собственных числах и собственных векторах корреляционной матрицы R, тогда как главные факторы опираются на такие же числа и векторы, но найденные для редуцированной ее формы R*. Отличие, таким образом, заключается в том, что главные компоненты описывали всю суммарную вариацию исходных признаков, тогда как главные факторы учитывают толь-ко суммарную общность этих признаков
tr R* = h12 + h22 + h32 + ... + hm2.
Первый главный фактор, таким образом, описывает максимум суммарной общности, второй - следующую по величине ее часть и т.д. Главные факторы нескоррелированы друг с другом, т.е. - являются ортогональными.
В связи с тем, что до нахождения нагрузок оценки общностей признаков можно получить только в приближенном виде, вычислительная процедура строится по итерационному принципу, изложенному в разделе 6.9. Здесь на каждом i-м шаге в результате нахождения собственных чисел и векторов матрицы R*i получается очередное приближение факторного отображения Ai. По нему находится следующее приближение общностей, которое вновь размещается на главной диагонали следующего приближения редуцированной матрицы R*i+1 и процесс продолжается до получения достаточно близких результатов.
Вследствие того, что на главной диагонали редуцированной корреляционной матрицы R*i стоят общности, которые по величине меньше 1, количество ненулевых собственных чисел n оказывается заметно меньше числа исходных признаков m (m > n). При этом остальные m - n собственных чисел равны нулю.
В результате применения факторизации по методу главных факторов, получаются значения n собственных чисел l1, l2, l3, ..., ln, и соответствующих им n собственных векторов a1, a2, a3, ..., an, включающих нагрузки. Иными словами, сумма квадратов элементов каждого вектора ai равна собственному числу li. Столбцы ai составляют матрицу факторного отображения A, которая также является одним из результатов вычислений. Кроме этого, по разным собственным числам находится факторная доля изменчивости
li
 Pi = . (6.38)
Pi = . (6.38)
m
Эта формула равносильна общему равенству (6.24).
6.13 Матрица факторного отображения A, получаемая по методу главных факторов, обычно имеет вид, сходный с нагрузками, которые можно найти при компонентном ана-
- 116 -
лизе. Если признаки связаны положительными корреляциями, как это характерно для большинства антропо-, остео- и краниометрических признаков, изучаемых по однородной выборке, первый фактор f1 имеет вектор a1, включающий положительные нагрузки той или иной величины. Тогда он называется генеральным фактором и по своей интер-претации близок к первой главной компоненте, которую можно было бы найти для этих данных. Остальные факторы f2, f3, ..., fn обычно имеют столбцы нагрузок a2, a3, ..., an с элементами разного знака для разных признаков. Поэтому, эти факторы называются - биполярными. Каждый из них по своим нагрузкам разделяет набор признаков на две части и описывает тем самым некоторый контраст формы примерно так же как это делали вторая, третья и т.д. главные компоненты.
6.14 В связи с тем, что в методе главных факторов до проведения вычислений не определено их количество, появляется та же проблема, которая возникала в компонентом анализе - вопрос о количестве новых переменных, которые следует учитывать для дальнейшей интерпретации. Для решения этой задачи в практике проведения факторного анализа используются все те же подходы, которые применяются при изучении главных компонент. Так, при работе со многими компьютерными программами очень часто до проведения вычислений можно задать минимальную величину собственного числа lmin, которое еще учитывается. Тогда в ходе вычислений нагрузки находятся только для тех главных факторов, у которых собственные числа больше этого минимума (li > lmin). Наиболее распространенным минимальным уровнем является lmin = 1, что фактически приводит к применению метода Кайзера (см. раздел 5.10). Иногда задается несколько меньшая величина lmin = 0.5, что приводит к более подробным, но и более громоздким результатам.
Другой подход к определению числа рассматриваемых факторов основан на применении критерия отсеивания Кеттела, изложенного в разделе 5.10. Здесь строится график значений всех n ненулевых собственных чисел (рис.5.4), на котором находится участок, где эти значения образуют пологую и примерно прямолинейную линию. Начало этой линии содержит собственное число, которое все еще должно учитываться при вычислении нагрузок на общие факторы.
Наконец, имеется подход, основанный на исследовании так называемой остаточной матрицы. Дело в том, что после получения матрицы факторного отображения A, учитывающей определенное количество факторов, можно выяснить насколько хорошо она описывает исходные данные. Для этой цели можно найти произведение
R^ = AA' , (6.39)
которое воспроизведет редуцированную корреляционную матрицу на основе ее описания результатами факторного анализа. Отличие этой формулы от аналогичного выражения (6.28) заключается в том, что здесь получается реально воспроизведенная на основе факторного отображения матрица корреляций R^, тогда как (6.29) дает теоретическое взаимоотношение между исходной матрицей R* и теми результатами, которые должны быть получены. Остаточная матрица Ro получается как мера несовпадения воспроизводимого результата R^ и исходных данных R*
Rо = R* - R^ . (6.40)
Остаточная матрица в качестве своих внедиагональных элементов содержит значения разностей roij = rij - r^ij эмпирических коэффициентов корреляции rij и воспроизведенных
-117 -
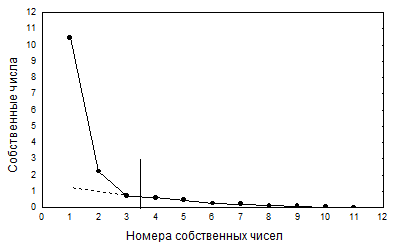
Рисунок 6.2. График значений собственных чисел, найденных при факторном анализе (главные факторы) 22 размеров тела в выборке 242 женщин
по результатам факторного анализа их величинами r^ij. Большинство компьютерных программ в качестве результатов факторного анализа выводят матрицу Rо.
Очевидно, что в ситуации, когда факторное решение адекватно описывает эмпирические данные, в остаточной матрице должны содержаться весьма малые значения разностей roij. Простейший способ определения малости разностей roij заключается в том, что они сравниваются с каким-то заведомо небольшим уровнем коррелированности, которым можно пренебречь - do. Тогда условием адекватности факторного решения будет выполнение roij < do. Обычно в качестве критического уровня выбирается do= 0.10. Во многих пакетах компьютерных программ, выводимые элементы остаточной матрицы отмечаются каким-то символом, если условие roij < do o не выполняется.
Более основательным способом рассмотрения остаточной матрицы является изучение величины варьирования, составляющих ее элементов. Если остаточные корреляции имеют заведомо случайную вариацию и не отличаются существенно от нулевого значения, то для них должны выполняться некоторые условия. Так, для их распределения должна быть характерна нормальная форма с нулевой средней и величиной дисперсии, находимой по формуле
 so2 = , (6.41)
so2 = , (6.41)
N - 2
где N - объем выборки. Таким образом, по всем m(m - 1)/2 остаточным корреляциям из матрицы Ro следует найти среднюю величину, дисперсию и получить гистограмму их значений. Для того, чтобы полученная матрица факторного отображения считалась адекватно и полно отражающей закономерности коррелированности признаков, необходимо, чтобы для средней величины Mro и дисперсии sro2, найденным по остаточным корреляциям roij, одновременно выполнялось
Mro » 0 (6.42)
sro2 » so2 .
- 118 -
Таблица 6.1. Результаты выделения главных факторов для 22 размеров тела по выборке 242 женщин.
| Признаки | Общности | |||
| 1.Длина корпуса | 0.113 | 0.441 | -0.174 | 0.243 |
| 2.Длина ноги | 0.235 | 0.741 | 0.413 | 0.812 |
| 3.Длина руки | 0.248 | 0.700 | 0.268 | 0.612 |
| 4.Акромиальный диаметр | 0.418 | 0.408 | -0.009 | 0.342 |
| 5.Тазогребневой диаметр | 0.733 | 0.296 | 0.068 | 0.625 |
| 6.Обхват груди | 0.912 | 0.008 | -0.124 | 0.832 |
| 7.Обхват живота | 0.906 | -0.066 | -0.078 | 0.817 |
| 8.Обхват бедра | 0.900 | -0.077 | 0.007 | 0.819 |
| 9.Обхват голени | 0.558 | -0.009 | -0.187 | 0.349 |
| 10.Обхват плеча | 0.879 | -0.077 | -0.128 | 0.788 |
| 11.Обхват предплечья | 0.815 | 0.092 | -0.188 | 0.711 |
| 12.Складка под лопаткой | 0.851 | -0.170 | 0.123 | 0.773 |
| 13.Складка на трицепсе | 0.874 | -0.219 | 0.118 | 0.824 |
| 14.Складка на бицепсе | 0.805 | -0.232 | 0.021 | 0.707 |
| 15.Складка на предплечьи | 0.846 | -0.202 | 0.037 | 0.757 |
| 16.Складка на животе | 0.855 | -0.197 | 0.187 | 0.812 |
| 17.Складка на бедре | 0.804 | -0.177 | 0.203 | 0.703 |
| 18.Складка на голени | 0.676 | -0.163 | 0.139 | 0.461 |
| 19.Ширина локтя | 0.323 | 0.342 | -0.190 | 0.261 |
| 20.Ширина запястья | 0.362 | 0.437 | -0.341 | 0.445 |
| 21.Ширина колена | 0.530 | 0.125 | -0.123 | 0.316 |
| 22.Ширина лодыжки | 0.409 | 0.283 | -0.162 | 0.274 |
| Собственное число | 10.43 | 2.19 | 0.71 | |
| Доля вариации (%) Pi | 47.43 | 9.95 | 3.23 | |
| Сумма Pi (%) | 47.43 | 57.38 | 60.61 |
Гистограмма значений roij при этом должна хотя бы приближенно воспроизводить нормальную кривую.
Пример 6.1 Рассмотрим пример проведения факторного анализа по методу главных факторов для 22 размеров тела по выборке 242 женщин. Эти данные нами ранее подвергались компонентному анализу в примере 5.1. При вычислениях были получены 11 собственных чисел, отличных от нуля. Их график приведен на рисунке 6.2, на котором можно видеть, что, начиная с третьего числа, образуется пологая и примерно прямолинейная последовательность. В соответствии с критерием отсеивания Кеттела можно считать, что следует рассматривать только три первых главных фактора. Их нагрузки приведены в
- 119 -
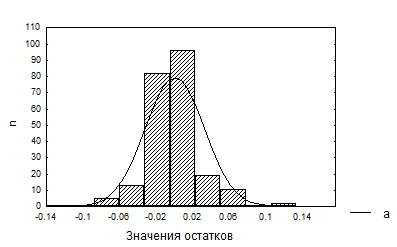
Рисунок 6.3. Гистограмма значений остаточных корреляций, найденных после учета трех главных факторов 22 размеров тела в выборке 242 женщин. Здесь: a - линия нормальной кривой
таблице 6.1. Там же находятся оценки общностей признаков, определенные в ходе итерационной процедуры.
Первый главный фактор имеет положительные нагрузки на все признаки. В наибольшей степени он скоррелирован с обхватами сегментов конечностей и жировыми складками. Здесь нагрузки имеют значения 0.56 - 0.91. Для скелетных размеров тела эти нагрузки имеют гораздо меньший уровень 0.24 - 0.53. Правда, тазогребневой диаметр по своим нагрузкам на первый главный фактор занимает промежуточное положение. Особняком стоит длина корпуса, которая практически не скоррелирована с первой главной компонентой. Поэтому, первый главный фактор может считаться интегративным показателем общей величины тела, в которой проявляется в первую очередь его поперечное развитие. При сравнении этих результатов с - полученными в примере 5.1, можно видеть их почти полное совпадение.
Второй главный фактор имеет биполярный характер. Положительные нагрузки характерны для скелетных размеров тела, где наибольшие величины 0.41 - 0.74 наблюдаются для длины корпуса и конечностей, акромиального диаметра и ширины запястья. Отрицательные нагрузки с величиной 0.16 - 0.23 характерны для жировых складок. Нетрудно видеть, что большие значения второго фактора можно будет обнаружить для индивидуальных вариантов с увеличенным продольным развитием скелетного компонента по отношению к жировому. Малые значения второго главного фактора будут наблюдаться у женщин, для которых будет характерно пониженное продольное развитие скелета при относительно повышенном развитии подкожного жира. Таким образом, второй фактор описывает общий продольно-поперечный контраст общей формы тела женщин. И здесь мы имеем полную аналогию с результатами компонентного анализа из примера 5.1.
Третий главный фактор - также биполярен и выделяет две группы признаков. Первую из них образуют продольные размеры конечностей с положительными нагрузками 0.27 - 0.41. Вторая группа признаков включает длину корпуса, диаметры локтя и запястья, обхваты голени и предплечья. Для них наблюдаются отрицательные нагрузки с ве-
- 120 -
личинами 0.17 - 0.34. Большие значения третьего фактора будут характерны для тех женщин, у которых относительно длинные конечности будут сочетаться с относительно коротким корпусом и ослабленным поперечным развитием скелетного компонента. Обратное сочетание относительно укороченных конечностей с удлиненным корпусом и усиленным развитием скелета даст малые значения третьего главного фактора. Таким образом, этот фактор описывает преимущественно контраст пропорций тела.
С какой степенью подробности выделение только первых трех факторов способно описать рассматриваемые корреляции признаков? Для ответа на этот вопрос для остаточной корреляционной матрицы, которая здесь не приводится из-за громоздкости, были найдены: средняя величина и дисперсия остаточных корреляций. Эти значения равны Mro = 0.000 и sro2 = 0.00102. Теоретическое значение дисперсии, определяемое через объем выборки по формуле (6.41), равно so2 = 0.00417. На рисунке 6.3 приведена гистограм-ма значений остаточных корреляций, найденных после учета трех главных факторов. Можно видеть, что форма их вариации примерно соответствует нормальной кривой. Таким образом, анализ остаточных коэффициентов корреляции показывает, что все три условия их малости соблюдается: средний их уровень практически равен 0, их дисперсия даже меньше теоретического случайного уровня, и форма распределения близка к нормальной.
6.15 При интерпретации матрицы факторного отображения, полученной для не слишком малого числа признаков, бывает не очень удобно рассматривать табличные данные, и всегда желательно получить эти результаты в графическом виде. Для этой цели используется так называемая векторная форма представления признаков. Ее суть заключается в следующем.
Пусть дано два признака. Тогда их можно изобразить в виде двух векторов, выходящих из одной точки. Их длины пропорциональны значениям их общностей, а угол a между представляющими векторами выбирается так, чтобы
cos a = r , (6.43)
где r - коэффициент корреляции между признаками. В случае m признаков можно получить пучок m векторов, лежащий в m-мерном пространстве. Длины этих векторов будут пропорциональны их общностям, а угол между любой парой i-го и j-го признаков будет определяться их коэффициентом корреляции в соответствии с формулой (6.43). Разумеется, эту картину нельзя представить в наглядном виде. Однако, можно определить проекцию m-мерного пучка векторов в пространство с гораздо меньшим числом осей, которым соответствуют факторы, описывающие основную долю информации о конфигурации этого пучка. Например, в случае двух факторов, можно построить векторный график на плоскости, трех факторов - в трехмерном пространстве.
Для сочетания двух факторов, координаты конечной точки любого вектора, представляющего i-й признак, определятся значениями двух его нагрузок a1i и a2i на факторы f1 и f2. Квадрат длины этого вектора будет равен a1i2 + a2i2 – общности hi2, а угол между ним и осью первого фактора будет определяться из равенства cos a = a1i, так как нагрузка a1i есть коэффициент корреляции между i-м признаком и фактором f1. В результате можно получить наглядную картину нагрузок всех m признаков на факторы f1 и f2. Эта картина может считаться отражением наиболее важной информации о взаимных корреляциях
- 121 -
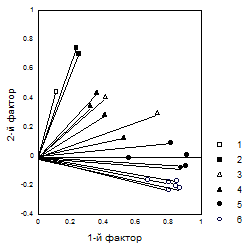
Рисунок 6.4. График нагрузок на первые два главных фактора для 22 размеров тела в выборке 242 женщин. Приняты обозначения: 1 - длина корпуса, 2 - длины ноги и руки, 3 - диаметры плеч и таза, 4 - диаметры мыщелков, 5 - обхваты сегментов тела, 6 - жировые складки
признаков. Иными словами, получив в осях факторов пучок векторов, представляющих признаки в соответствии с их нагрузками, можно считать, что мы наглядно увидим то наиболее важное, что проявляется во взаимном расположении m векторов, представля-ющих признаки. Такого рода графики часто строятся автоматически при проведении факторного анализа. Правда, обычно на них бывают представлены только конечные точки векторов, соответствующих признакам.
В ситуации, когда выделяются только два фактора, достаточно одного графика, представляющего факторное отображение в осях двух факторов f1 и f2. Когда выделяются три фактора f1, f2 и f3, можно построить единый трехмерный график, представляющий конечные точки векторов, соответствующих признакам, в пространстве факторных осей. Кроме этого, можно построить три двумерных графика, изображающих векторы признаков в попарных сочетаниях осей f1 и f2, f1 и f3, f2 и f3. Из них наиболее информативной будет первая картина, так как наиболее важную информацию о корреляциях признаков несут первые два фактора.
Пример 6.2 Построим графики нагрузок на 22 размера тела, полученные по методу главных факторов в примере 6.1. На рисунке 6.4 приведено расположение векторов, представляющих признаки в осях первых двух факторов, совместно описывающих 57.4% суммарной вариации рассматриваемых размеров тела. Неплохо видно противопоставление двух групп признаков, первую из которых образуют продольные размеры корпуса и конечностей, вторую - жировые складки. Обхватные размеры сегментов тела близки к последним, но занимают более нейтральное положение. Поперечные скелетные диаметры занимают промежуточное положение между продольными размерами тела и обхватами, зависящими в своем развитии от мягких тканей. Тазогребневой диаметр из всех поперечных скелетных размеров тела наиболее приближен к обхватам.
- 122 -
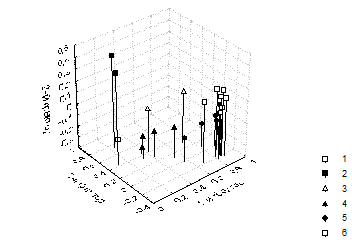
Рисунок 6.5. График нагрузок на три главных фактора для 22 размеров тела в выборке 242 женщин. Приняты обозначения: 1 - длина корпуса, 2 - длины ноги и руки, 3 - диаметры плеч и таза, 4 - диаметры мыщелков, 5 - обхваты сегментов тела, 6 - жировые складки
На рисунке 6.5 приведен график нагрузок на все три фактора. Здесь для простоты представлены не векторы, а их конечные точки. Можно видеть, что картина расположения конечных точек векторов признаков для первых двух факторов (рис.6.4) здесь модифицируется в соответствии с нагрузками на третью ось, противопоставляя продольные размеры конечностей, диаметрам мыщелков конечностей.
Дата добавления: 2016-02-13; просмотров: 3426;
