Ортогональное преобразование факторных решений
6.20 Факторы, получаемые по одному из методов факторизации, обладают опре-деленными заданными свойствами. Они могут максимально полно описывать общности признаков (главные факторы), или исчерпывающе учитывать корреляции признаков (факторы минимальных остатков) или быть хорошими статистическими оценками (максимально правдоподобные факторы). Все эти математические свойства далеко не исчерпывают те желательные качества факторного отображения, которые следовало бы достичь. Одним из таких свойств является интерпретируемость факторного решения.
- 129 -
В приведенных примерах результаты факторного анализа можно было истолковывать в терминах вариации общего размера и формы тела. Однако, такая относительно ясная картина в практике применения факторного анализа встречается далеко не всегда, и проблема интерпретируемости факторного решения может оказаться наиболее важной при его использовании. Набор приемов, входящих в факторный анализ, включает инструменты, позволяющие преобразовывать факторные отображения с целью их более легкого истолкования.
Матрица факторного отображения A имеет n столбцов нагрузок для m признаков, и может включать от нескольких десятков до нескольких сотен элементов aij. Эти элементы могут различаться по абсолютной величине от близких 1 до практически равных 0. При их истолковании логично обращать внимание в первую очередь на значительные элементы aij, тогда как близкие к нулю нагрузки игнорируются.
Очевидно, что рассмотрение и визуальный анализ матрицы отображения A будет тем проще, чем меньше нагрузок будут иметь большие по абсолютной величине значения и чем больше нагрузок окажутся близкими к нулю. В результате первоначальной факторизации такие результаты обычно не получаются, но их можно достичь при помощи специального преобразования факторов. В разделе 6.10 мы видели, что с применением специальной трансформационной матрицы T исходное факторное отображение A1 может быть преобразовано к новому решению A2 = A1T. При этом исходные факторы f1 связаны с новой их системой равенством f1 = f2T.
Эти преобразования могут преследовать цель получения в матрице A2 достаточно большого числа нулевых нагрузок и относительно малого количества нагрузок со значительной абсолютной величиной. Тогда A2 будет характеризоваться простотой своей структуры, удобной для рассмотрения и интерпретации. Условия существования простой структуры в матрице A2 были сформулированы Л.Терстоном, выделившим следующие пять ее критериев.
1.Каждая строка матрицы A2, включающая нагрузки одного признака на все факторы, должна иметь по крайней мере один нулевой элемент.
2.Каждый столбец матрицы A2, включающий нагрузки всех признаков на один фактор, должна иметь не менее n нулевых элементов, где n - число факторов.
3.В любой паре столбцов матрицы A2, включающий нагрузки всех признаков на любые два фактора, должны иметься признаки, одна из нагрузок которого имеет большую абсолютную величину, другая - близкую к нулю.
4.В любой паре столбцов матрицы A2, включающий нагрузки всех признаков на любые два фактора, должны иметься признаки, обе нагрузки которого близки к нулю.
5.В любой паре столбцов матрицы A2, включающий нагрузки всех признаков на любые два фактора, только небольшое число признаков может иметь значительные нагрузки на оба этих фактора.
Способ ортогонального преобразования двух факторных осей с целью достижения простого вида новой матрицы A2 иллюстрирует рисунок 6.6. При помощи факторизации были выделены два фактора f1 и f2, первый из которых - генеральный с положительными нагрузками на него у всех признаков, второй - биполярный, выделяющий две группы признаков 1 и 2. Очевидно, что в исходной матрице факторного отображения A1 все m * n нагрузок - велики. Повернем факторные оси так, чтобы одна из них прошла бы
- 130 -
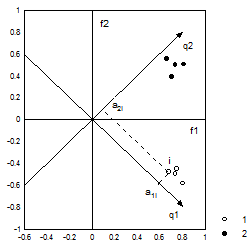
Рисунок 6.6. Принцип ортогонального вращения исходных факторных осей f1 и f2 к новым координатам факторов q1 и q2. Приняты обозначения: a1i и a2i – нагрузки i-го признака на новые факторы q1 и q2, 1 и 2 - признаки из двух разных групп
по возможности как можно ближе к центру 1-й группы точек, представляющих признаки, а вторая - к центру 2-й такой группы.
Пусть угол этого поворота осей равен j. Очевидно, в новой системе осей q1 и q2 нагрузки на признаки, которые можно найти как проекции точек на эти оси, будут иметь простую структуру. Действительно, для некоторого i-го признака, нагрузка a1i на первый новый фактор q1 будет большой, тогда как нагрузка a2i на q2 окажется малой. В результате, фактор q1 будет описывать корреляции одной группы признаков, а фактор q2 учтет взаимосвязи другой такой группы. Как это можно видеть на рисунке 6.6, в матрице A2, включающей нагрузки на новые факторные оси q1 и q2, большими по абсолютной величине будут только m нагрузок, тогда как остальные - окажутся близкими к нулю.
Новая матрица A2 может быть в соответствии с принципами аналитической геометрии найдена по формуле A2 = A1T, где матрица трансформации Tопределяется углом поворота факторных осей f
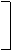
 cos j -sin j
cos j -sin j
T = . (6.48)
sin j cos j
Переход от первоначальных ортогональных факторных координат к новым также взаимно перпендикулярным осям, не изменяет ортогональности трансформированных факторов с матрицей отображения A2. Эта процедура называется ортогональной ротацией факторов.
Следует заметить, что ротация факторных осей никак не затрагивает взаимного расположения векторов, проставляющих исходные признаки. Конфигурация этих векторов, с их взаимными угловыми характеристиками и их длинами, определяется только корреляциями и общностями соответствующих им признаков. Преобразование же системы координат направлено на более ясное и более удобно истолковываемое размещение пучка всех этих векторов.
- 131 -
6.21 В случае количества факторов большем двух (n > 2), ситуация принципиально не изменится, хотя станет более громоздкой. В этом случае требуется осуществить n(n –
- 1)/2 вращений попарных сочетаний факторов. Пусть имеется три общих фактора с матрицей факторного отображения A1, включающей три столбца нагрузок a11, a12 и a13. Необходимо при помощи поворотов осей перейти к простой матрице A2, включающей столбцы a21, a22 и a23.
Вначале проводится поворот первых двух факторов. Пусть величина угла поворота равна j12. Матрица трансформации для этого поворота в соответствии с формулой (6.48) имеет вид
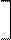
 cos j12 -sin j12 0
cos j12 -sin j12 0
T12 = sin j12 cos j12 0 .
0 0 0
Нулевые ее элементы соответствуют неучастию во вращении третьего фактора. В результате поворота получается так называемая первая промежуточная матрица
B1 = A1T12 ,
состоящая из трех столбцов нагрузок b11, b12 и a13. Первые два из них включают преобразованные нагрузки, третий - исходные элементы матрицы A1 , не участвовавшие во вращении.
На втором этапе вращения преобразуется сочетание нагрузок первого повернутого и третьего исходного факторов со столбцами b11 и a13, тогда как второй преобразованный фактор и соответствующий ему столбец b12 остаются без изменений. В результате поворота получается так называемая вторая промежуточная матрица
B2 = B1T13 ,
состоящая из трех столбцов нагрузок b21, b12 и b23. Угол поворота j13 определит вторую трансформационную матрицу

 cos j13 0 -sin j13
cos j13 0 -sin j13
T13 = 0 0 0 .
sin j13 0 cos j13
Второй, преобразованный в первом вращении, фактор с нагрузками b12 в этой ротации не участвует.
Наконец, на третьем этапе преобразуется сочетание второго и третьего факторов с нагрузками b12 и b23. Первый фактор с нагрузками b21 в этом вращении не участвует. Угол последнего поворота j23 определяет третью трансформационную матрицу

 0 0 0
0 0 0
T23 = 0 cos j23 -sin j23 ,
0 sin j23 cos j23
при помощи которой получается окончательная матрица нагрузок
A2 = B2T23 ,
состоящая из трех столбцов a21, a22 и a23. Первый из них a21 - равен столбцу b21, найденному на втором этапе преобразований.
При ротации четырех факторов число этапов вращения увеличивается до шести. Последовательно находятся углы поворота j12, j13, j14, ..., j34, которым соответствуют трансформационные матрицы
- 132 -

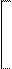 cos j12 -sin j12 0 0
cos j12 -sin j12 0 0
T12 = sin j12 cos j12 0 0 ,
0 0 0 0
0 0 0 0

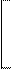 cos j13 0 -sin j13 0
cos j13 0 -sin j13 0
T13 = 0 0 0 0
sin j13 0 cos j13 0 ,
0 0 0 0
... ... ... ...

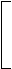 0 0 0 0
0 0 0 0
T34 = 0 0 0 0
0 0 cos j34 -sin j34
0 0 sin j34 cos j34
С их использованием последовательно находятся промежуточные матрицы нагрузок B1= = A1T12, B2 = B1T13, B3 = B2T14, ..., A2 = B5T34.
6.22 Проблема ортогональной ротации факторных осей сводится, таким образом, к нахождению углов поворота, обеспечивающих такие вращения этих осей, которые обеспечивают достижение наибольшей простоты окончательной матрицы A2. На ранних этапах развития техники факторного анализа для этих целей использовалось построение точных графиков всех исходных и промежуточных результатов ротации с прямым измерением углов поворотов. В настоящее время эти операции осуществляются с применением аналитических методов вращения. Их суть - в многократном итеративном вращении осей, в результате чего достигается максимум некоторой функции, отражающей простоту получающейся матрицы преобразованных нагрузок. В зависимости от принципов построения этих функций получаются различные методы ортогональной ротации.
Критерий простоты получаемого в результате ротации факторного отображения может основываться на следующих соображениях. Для достижения этой простоты, требуется, чтобы для каждого i-го признака строка его нагрузок a2ji на все повернутые факторы (j = 1, 2, ... n) содержала бы только либо большие по абсолютной величине, либо близкие к нулю значения. Тогда сумма четвертых степеней его нагрузок
n
Qi = S a2ji4
j = 1
будет тем больше, чем ближе к 1 будут крупные по абсолютной величине нагрузки. При возведении в 4-ю степень значения средних и малых нагрузок уменьшатся весьма значительно, тогда как для больших a2ji это уменьшение окажется не столь сильным. Например, 4-я степень нагрузки a2ji= 0.9 равна 0.66, тогда как для для a2ji = 0.5 она составит всего - 0.06. Поэтому, в качестве возможной функции, отражающей простоту ротиро-ванной факторной структуры, может быть выражение
m m n
Q = S Qi = S S a2ji4 = max . (6.49)
i = 1 i = 1 j = 1
- 133 -
С другой стороны, в случае простой структуры ротированного факторного отображения, сопровождающейся присутствием в ней большого числа почти нулевых нагрузок, для каждого i-го признака сумма попарных произведений его нагрузок на все n преобразованные факторы
n
Pi = S a2ji a2ki
k < j = 1
будет минимальной. Это позволяет получить другой вид критерия простоты ротированного факторного отображения
m m n
P = S Pi = S S a2ji a2ki = min . (6.50)
i = 1 i = 1 k<j=1
Критерии (6.49) и (6.50) тесно связаны друг с другом. Дело в том, что при проведении ротации общности признаков не изменяются. С учетом равенства (6.23) это можно записать в виде выражения для общности каждого i-го признака
n n
hi2 = S a1ji2 = S a2ji2 ,
j = 1 j = 1
где a1ji - нагрузка i-го признака на j-й фактор для исходного факторного отображения, a2ji - аналогичная нагрузка для преобразованных путем ротации факторов. Квадрат общности (hi2)2 также не изменится в результате ротации, что для нагрузок на ротированные факторы можно записать в виде формулы
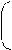
 n 2 n n
n 2 n n
(hi2)2 = S a2ji2 = S a2ji4 + 2 S a2ji a2ki = const.
j = 1 j = 1 k<j=1
Просуммировав это выражение для всех m признаков, можно получить
m n m n
S S a2ji4 + 2 S S a2ji a2ki = Q + 2P = const.
i = 1 j = 1 i = 1 k<j=1
Последнее означает, что для соблюдения постоянства суммы квадратов общностей для всех исходных признаков требуется, чтобы при достижении максимума величины Q, одновременно достигался бы минимум критерия P. Поэтому, оказывается безразличным, будет ли при вычислениях максимизироваться критерий Q, или минимизироваться функция P. Метод аналитической ортогональной ротации, основанный на применении любого из этих критериев, называется методом квартимакс.
В соответствии с этим методом по исходным нагрузкам находятся значения углов поворота j12, j13, j14, ... и т.д., по которым в соответствии с разделом 6.21 осуществляются необходимые n(n - 1)/2 ротаций факторов. Со способом определением углов j можно познакомиться по книге Г.Хармана (1972). Как правило, одного цикла n(n - 1)/2 таких поворотов бывает недостаточно для достижения условия Q = max или P = min. Поэтому, процесс ротации неоднократно повторяется до тех пор, пока эти условия не будут достиг-нуты.
- 134 -
6.23 Аналитическое вращение факторов по методу квартимакс направлено на упрощение вида строк матрицы факторного отображения - на оптимизацию описания отдельных признаков. При этом не достигается простой вид столбцов этой матрицы, соответствующих нагрузкам на отдельные факторы. Это приводит к появлению при использовании квартимакс-ротации сильной тенденции к выделению первого преобразованного фактора сходного с генеральным фактором, находимым непосредственно в результате факторизации.
Напомним, что при получении исходных факторных отображений при помощи методов главных факторов, минимальных остатков или максимума правдоподобия всегда выявлялся первый фактор, описывающий значительную долю суммарной вариации признаков и имеющий высокие нагрузки на все или большинство рассматриваемых признаков. Он учитывает наиболее важное направление коррелированности признаков. Наличие генерального фактора, имеющего значительные нагрузки на все или большинство признаков, по своему смыслу прямо противоположно принципу простой структуры факторного отображения, и тенденция к его выделению в ходе квартимакс-ротации считается недостатком этого метода.
Попытка добиться упрощения вида наборов нагрузок на факторы привела к разработке так называемого метода варимакс Кайзера. Простота j-го столбца ротированной матрицы, соответствующего j-му повернутому фактору, будет тем большей, чем больше в нем будет максимально больших и предельно малых по абсолютной величине нагрузок a2ji. Иными словами, простой вид столбца нагрузок должен характеризоваться максимальной вариацией их абсолютных значений. Эта вариация может быть описана дисперсией квадратов нагрузок
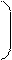
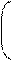 1 m 1 m 2
1 m 1 m 2

 saj2 = S (a2ji2)2 - S a2ji2 .
saj2 = S (a2ji2)2 - S a2ji2 .
m i = 1 m2 i = 1
Для всех n факторов наибольшая простота их нагрузок будет достигаться при максимальном значении сумм этих дисперсий
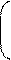
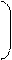 n 1 n m 1 n m 2
n 1 n m 1 n m 2

 V = Ssaj2 = S S (a2ji2)2 - S S a2ji2 = max . (6.51)
V = Ssaj2 = S S (a2ji2)2 - S S a2ji2 = max . (6.51)
j = 1 m j = 1 i = 1 m2 j = 1 i = 1
Формула (6.51) обладает недостатком, связанным с тем, что участие в ней признаков с большими общностями оказывается более заметным по сравнению с теми исходными показателями, общности которых - невелики. Для его устранения нагрузки всех признаков нормируются по Кайзеру на значения общностей
a2ji2
 b2ji2 = , (6.52)
b2ji2 = , (6.52)
hi2
и в формуле критерия (6.51) используются вместо a2ji2 величины b2ji2 . В результате получается нормированный варимакс критерий
 1 n m 1 n m 2
1 n m 1 n m 2

 Vh = S S (b2ji2)2 - S S b2ji2 = max . (6.53)
Vh = S S (b2ji2)2 - S S b2ji2 = max . (6.53)
m j = 1 i = 1 m2 j = 1 i = 1
- 135 -
Проведение варимакс-преобразования факторов сводится к определению углов поворота j12, j13, j14, ... и т.д., по которым в соответствии с разделом 6.21 осуществляются необходимые n(n - 1)/2 ротаций факторов. Способ определения углов j можно найти в книге Г.Хармана (1972). Обычно такие циклы ротаций осуществляются многократно до тех пор пока не будет достигнут максимум критерия (6.53). В соответствии с двумя видами варимакс-критерия (6.51) и (6.53) различают два вида этой ротации - нормированную и ненормированную. Обычно применяется - вторая. Аналогичным образом, нормированные нагрузки (6.52) могут применяться и при проведении вращений факторов по методу квартимакс, что точно также дает две его модификации - нормированную и ненормированную. В последнем случае применяется критерий
m n
Qh = S S b2ji4 = max . (6.54)
i = 1 j = 1
Существуют также методы ортогонального преобразования факторов которые объединяют свойства способов квартимакс и варимакс. При их использовании применяется обобщенный критерий
Wh = aQh + bVh = max ,
который также может быть записан в виде

 n m g n m 2
n m g n m 2
 Wh = S S (b2ji2)2 - S S b2ji2 = max , (6.55)
Wh = S S (b2ji2)2 - S S b2ji2 = max , (6.55)
j = 1 i = 1 m j = 1 i = 1
где
b
 g = .
g = .
a + b
Если g = 0 , обобщенный критерий превращается в критерий квартимакс, при g = 1, он становится варимакс-критерием. При g = 0.5 получается особый биквартимакс-критерий. Наконец, при g = n/2 обобщенная формула дает эквимакс-критерий. Методы биквартимакс и эквимакс должны по своему смыслу давать результаты ротации, промежуточные между теми, которые получаются с использованием критериев квартимакс и варимакс.
В практике ортогонального вращения факторных осей наиболее часто используется варимакс-ротация.
Пример 6.5 Проведем ортогональное преобразование матрицы факторного отображения, найденной с применением метода главных факторов для 22 размеров тела по выборке 242 женщин из примера 6.1. Ротация осуществлялась с использованием четырех методов: квартимакс, варимакс, биквартимакс и эквимакс. Применялись нормированные формы критериев.
Для результатов, полученных при ротации факторов с использованием всех четырех методов наблюдается очевидное сходство. Первый ротированный фактор во всех случа-ях (табл.6.5- 6.6) имеет максимальные нагрузки на обхватные размеры сегментов тела и жировые складки. При этом остальные признаки связаны с ним намного слабее. Однако, при сравнении результатов, полученных при разных способах вращения, для этого
- 136 -
фактора можно отметить, что нагрузки для других признаков имеют разную величину. Так, для акромиального диаметра варимакс-решение имеет на первом факторе нагрузку 0.24, тогда как три остальных метода - 0.30 - 0.35. Для тазогребневого диаметра нагрузка на первый варимакс-фактор равна 0.59, а для трех остальных результатов аналогичная величина составляет 0.64 - 0.68. То же самое можно наблюдать и для обхватов голени и предплечья, где варимакс-нагрузки равны соответственно 0.49 и 0.70, что меньше 0.53 - 0.55 и 0.75 - 0.79, найденных для трех остальных вращений. То же самое характерно и для ширины колена. Иными словами, первый варимакс-фактор имеет заметно меньшие нагрузки на признаках, не относящиеся к системе поперечных размеров тела, зависящих у женщин в первую очередь от развития жироотложения.
Второй фактор для всех четырех результатов вращения имеет наибольшие нагрузки у продольных размеров конечностей. В наибольшей степени это характерно именно для результатов варимакс-ротации (табл.6.5). Здесь длины ноги и руки имеют нагрузки 0.86 и 0.70, тогда как для трех остальных результатов первый признак демонстрирует нагрузки 0.81 - 0.83, а второй 0.64 - 0.66.
Третий фактор может расцениваться как описывающий общее развитие скелета, так как он имеет нагрузки 0.3 - 0.6 для габаритных размеров скелета и диаметров мыщелков. Для результатов ротации по методу варимакс и биквартимакс можно найти также небольшое участие в вариации третьего фактора у обхватов, зависящих в своем развитии от жирового и мышечного компонента. Так как нагрузки жировых складок на третий варимакс-фактор практически равны нулю, можно сделать вывод, что участие обхватов сегментов тела в вариации третьего фактора связано с мышечным компонентом. Таким образом, третий фактор, полученный по методам варимакс и биквартимакс, описывает также поперечное развитие мускулатуры. Правда, для третьего фактора, полученного при помощи остальных двух способов ротации, участие мышечного компонента не свойственно.
Подобные различия нагрузок обхватов сегментов тела на третий фактор, определенных по разным способам ротации, могут быть связаны с некоторыми свойствами самих методов вращения. Так, для квартимакс ротации характерно стремление к упрощению описания ротированных нагрузок для признаков, а не для факторов. При этом проявляется склонность этого метода к выявлению фактора, похожего на - генеральный, обычно выделяющийся в ходе факторизации. Можно заметить (табл.6.5), что для первого квартимакс-ротированного фактора нагрузки у большинства признаков действительно выше, чем у аналогичных результатов для преобразований по методам варимакс и биквартимакс. Склонность квартимакс-критерия выделять генеральный фактор проявляется также и в том, что первый квартимакс-фактор описывает 46.3% суммарной вариации признаков, тогда как аналогичные доли для методов варимакс и биквартимакс равны соответственно 41.9% и 44.7%.
Таким образом, описывая необоснованно большую долю вариации и коррелирован-ности исходных признаков первым преобразованным фактором, метод квартимакс-ротации соответствующим образом уменьшает аналогичные доли, приходящиеся на второй и третий повернутые факторы, что может преуменьшить нагрузки многих признаков на них. По-видимому, с этим эффектом связано слабое участие обхватов сегментов тела на третьем факторе. Результаты ротации по методам квартимакс и эквимакс оказа-
- 137 -
Таблица 6.5. Результаты квартимакс и варимакс ротации
| Признаки | |||
| Квартимакс-факторы | |||
| 1.Длина корпуса | 0.039 | 0.126 | 0.475 |
| 2.Длина ноги | 0.131 | 0.814 | 0.361 |
| 3.Длина руки | 0.146 | 0.643 | 0.421 |
| 4.Акромиальный диаметр | 0.350 | 0.262 | 0.387 |
| 5.Тазогребневой диаметр | 0.680 | 0.288 | 0.279 |
| 6.Обхват груди | 0.893 | -0.001 | 0.183 |
| 7.Обхват живота | 0.899 | -0.009 | 0.097 |
| 8.Обхват бедра | 0.903 | 0.017 | 0.062 |
| 9.Обхват голени | 0.547 | -0.119 | 0.187 |
| 10.Обхват плеча | 0.876 | -0.069 | 0.124 |
| 11.Обхват предплечья | 0.787 | -0.037 | 0.300 |
| 12.Складка под лопаткой | 0.871 | 0.067 | -0.100 |
| 13.Складка на трицепсе | 0.901 | 0.011 | -0.113 |
| 14.Складка на бицепсе | 0.833 | -0.067 | -0.084 |
| 15.Складка на предплечьи | 0.867 | -0.044 | -0.053 |
| 16.Складка на животе | 0.881 | 0.100 | -0.159 |
| 17.Складка на бедре | 0.824 | 0.086 | -0.128 |
| 18.Складка на голени | 0.676 | 0.005 | -0.056 |
| 19.Ширина локтя | 0.260 | 0.063 | 0.435 |
| 20.Ширина запястья | 0.281 | 0.007 | 0.605 |
| 21.Ширина колена | 0.500 | 0.002 | 0.255 |
| 22.Ширина лодыжки | 0.357 | 0.071 | 0.376 |
| Доля вариации (%) Pi | 46.344 | 5.929 | 8.146 |
| Варимакс-факторы | |||
| 1.Длина корпуса | -0.073 | 0.194 | 0.447 |
| 2.Длина ноги | 0.019 | 0.864 | 0.253 |
| 3.Длина руки | 0.026 | 0.704 | 0.340 |
| 4.Акромиальный диаметр | 0.244 | 0.337 | 0.410 |
| 5.Тазогребневой диаметр | 0.589 | 0.369 | 0.375 |
| 6.Обхват груди | 0.827 | 0.082 | 0.373 |
| 7.Обхват живота | 0.852 | 0.063 | 0.294 |
| 8.Обхват бедра | 0.864 | 0.085 | 0.256 |
| 9.Обхват голени | 0.493 | -0.055 | 0.319 |
| 10.Обхват плеча | 0.826 | 0.006 | 0.323 |
| 11.Обхват предплечья | 0.698 | 0.057 | 0.468 |
| 12.Складка под лопаткой | 0.868 | 0.109 | 0.085 |
| 13.Складка на трицепсе | 0.902 | 0.054 | 0.087 |
| 14.Складка на бицепсе | 0.832 | -0.024 | 0.112 |
| 15.Складка на предплечьи | 0.857 | 0.005 | 0.146 |
- 138 -
Таблица 6.5. (Продолжение)
| Признаки | |||
| 16.Складка на животе | 0.891 | 0.134 | 0.025 |
| 17.Складка на бедре | 0.828 | 0.121 | 0.045 |
| 18.Складка на голени | 0.671 | 0.041 | 0.094 |
| 19.Ширина локтя | 0.152 | 0.141 | 0.467 |
| 20.Ширина запястья | 0.135 | 0.111 | 0.644 |
| 21.Ширина колена | 0.429 | 0.071 | 0.356 |
| 22.Ширина лодыжки | 0.259 | 0.147 | 0.431 |
| Доля вариации (%) Pi | 41.873 | 7.569 | 10.977 |
Таблица 6.6. Результаты биквартимакс и эквимакс ротации
| Признаки | |||
| Биквартимакс-факторы | |||
| 1.Длина корпуса | -0.012 | 0.147 | 0.470 |
| 2.Длина ноги | 0.077 | 0.832 | 0.335 |
| 3.Длина руки | 0.089 | 0.664 | 0.403 |
| 4.Акромиальный диаметр | 0.303 | 0.287 | 0.408 |
| 5.Тазогребневой диаметр | 0.642 | 0.316 | 0.334 |
| 6.Обхват груди | 0.869 | 0.027 | 0.273 |
| 7.Обхват живота | 0.884 | 0.016 | 0.189 |
| 8.Обхват бедра | 0.891 | 0.042 | 0.153 |
| 9.Обхват голени | 0.527 | -0.097 | 0.248 |
| 10.Обхват плеча | 0.860 | -0.042 | 0.216 |
| 11.Обхват предплечья | 0.752 | -0.004 | 0.380 |
| 12.Складка под лопаткой | 0.875 | 0.084 | -0.013 |
| 13.Складка на трицепсе | 0.907 | 0.028 | -0.020 |
| 14.Складка на бицепсе | 0.839 | -0.050 | 0.004 |
| 15.Складка на предплечьи | 0.868 | -0.025 | 0.037 |
| 16.Складка на животе | 0.891 | 0.114 | -0.073 |
| 17.Складка на бедре | 0.831 | 0.100 | -0.046 |
| 18.Складка на голени | 0.678 | 0.018 | 0.012 |
| 19.Ширина локтя | 0.212 | 0.089 | 0.456 |
| 20.Ширина запястья | 0.216 | 0.041 | 0.630 |
| 21.Ширина колена | 0.471 | 0.026 | 0.305 |
| 22.Ширина лодыжки | 0.314 | 0.096 | 0.407 |
| Доля вариации (%) Pi | 44.748 | 6.404 | 9.268 |
| Эквимакс-факторы | |||
| 1.Длина корпуса | 0.039 | 0.126 | 0.475 |
| 2.Длина ноги | 0.131 | 0.814 | 0.361 |
| 3.Длина руки | 0.146 | 0.643 | 0.421 |
- 139 -
Таблица 6.6. (Продолжение)
| Признаки | |||
| 4.Акромиальный диаметр | 0.350 | 0.262 | 0.387 |
| 5.Тазогребневой диаметр | 0.680 | 0.288 | 0.279 |
| 6.Обхват груди | 0.893 | -0.001 | 0.183 |
| 7.Обхват живота | 0.899 | -0.009 | 0.097 |
| 8.Обхват бедра | 0.903 | 0.017 | 0.062 |
| 9.Обхват голени | 0.547 | -0.119 | 0.187 |
| 10.Обхват плеча | 0.876 | -0.069 | 0.124 |
| 11.Обхват предплечья | 0.787 | -0.037 | 0.300 |
| 12.Складка под лопаткой | 0.871 | 0.067 | -0.100 |
| 13.Складка на трицепсе | 0.901 | 0.011 | -0.113 |
| 14.Складка на бицепсе | 0.833 | -0.067 | -0.084 |
| 15.Складка на предплечьи | 0.867 | -0.044 | -0.053 |
| 16.Складка на животе | 0.881 | 0.100 | -0.159 |
| 17.Складка на бедре | 0.824 | 0.086 | -0.128 |
| 18.Складка на голени | 0.676 | 0.005 | -0.056 |
| 19.Ширина локтя | 0.260 | 0.063 | 0.435 |
| 20.Ширина запястья | 0.281 | 0.007 | 0.605 |
| 21.Ширина колена | 0.500 | 0.002 | 0.255 |
| 22.Ширина лодыжки | 0.357 | 0.071 | 0.376 |
| Доля вариации (%) Pi | 46.344 | 5.929 | 8.146 |
лись весьма сходными. На рисунках 6.7 - 6.8 приведены наглядные графики, соответству-ющие результатам варимакс-ротации. Здесь представлены сочетания 1-го преобразован-ного фактора со 2-м и 3-м.
Пример 6.6 Рассмотрим выполнение факторного анализа с проведением ортогональной ротации для набора 20 размеров черепа. Материалом для анализа послужила объединенная краниологическая выборка (N = 390), составленная из нескольких отдельных небольших серий черепов. Перед объединением этих серий внутри каждой из них проводилась нормировка всех признаков, что устранило межгрупповую неоднородность и позволяло свести все материалы в единую выборку.
При факторизации по методу главных факторов были найдены 9 ненулевых собственных чисел, приведенных на рисунке 6.9. Можно видеть, что пологий и приблизительно прямолинейный участок последовательности этих чисел начинается с 4-го из них. Поэтому, в соответствии с критерием отсеивания Кеттела можно считать, что необходимо рассматривать 4 фактора, которые совместно описывают 45.6% суммарной вариации признаков, что - заметно меньше по сравнению с аналогичными результатами, получавшимися для размеров тела. Это связано с общим менее высоким уровнем взаимной коррелированности признаков черепа.
Первый главный фактор (табл.6.7) имеет положительные нагрузки на все признаки и, таким образом, описывает интегративную величину черепа. Наибольшие значения на-
- 140 -
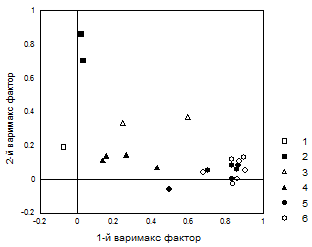
Рисунок 6.7. График нагрузок на 1-й и 2-й варимакс факторы для 22 размеров тела в выборке 242 женщин. Обозначения: 1 - длина корпуса, 2 - длины ноги и руки 3 – диамет-ры плеч и таза, 4 - диаметры мыщелков, 5 - обхваты сегментов тела, 6 - жировые складки
грузок на первый фактор можно отметить для поперечных размеров лица и нейрокраниума: верхней ширины лица, биорбитального диаметра, скулового диаметра, наименьшей ширины лба, средней ширины лица, ширины орбиты и ширины черепа. Таким образом, первый главный фактор описывает в первую очередь широтное развитие черепа.
Второй главный фактор - биполярен и по противоположным нагрузкам выделяет две группы признаков. Первую составляют поперечный диаметр черепа, наибольший лобный диаметр, и ширина основания черепа. Вторая группа признаков образована высотами лица
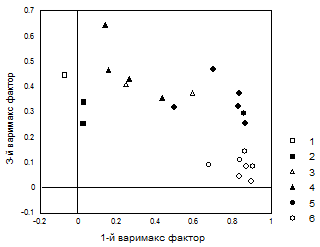
Рисунок 6.8. График нагрузок на 1-й и 3-й варимакс факторы для 22 размеров тела в выборке 242 женщин. Приняты обозначения: 1 - длина корпуса, 2 - длины ноги и руки, 3 - диаметры плеч и таза, 4 - диаметры мыщелков, 5 - обхваты сегментов тела, 6 - жировые складки
- 141 -
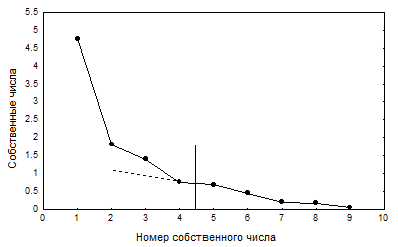
Рисунок 6.9. График значений собственных чисел, найденных при факторном анализе (главные факторы) 20 размеров черепа
и грушевидного отверстия, длинами основания лица и неба. Таким образом, второй глав-ный фактор описывает контраст формы черепа, где поперечное развитие нейрокраниума противостоит продольному и сагиттальному развитию висцеральной части черепа. По предельным значениям второго фактора можно выделить два полярных варианта, первый из которых будет характеризоваться большими значениями фактора и сочетанием относительно широкой мозговой коробки при относительно невысоком и коротком лице. Обратная комбинация узкого нейрокраниума, высокого и удлиненного в сагиттальном направлении лица будет наблюдаться для малых значений второго фактора.
Третий фактор - также биполярен и выделяет две группы признаков, одну из которых образуют длина основания лица и размеры неба, к которым примыкает ширина грушевидного отверстия. Вторая группа исходных переменных включает верхнюю высоту лица, высоты орбиты и грушевидного отверстия. Таким образом, третий главный фактор описывает контраст формы лицевой части черепа, где высотное ее размеры противопоставлены развитию преимущественно верхней челюсти. Полярные варианты, соответствующие предельным значениям третьего фактора - таковы, что большим его значениям соответствует сочетание относительно увеличенного сагиттального развития лица и крупных размеров неба с невысоким лицом, орбитами и грушевидным отверстием. Малым значениям третьего фактора соответствует комбинация относительно короткого лица с небольшими размерами неба и относительно больших высот лица, орбит и грушевидного отверстия. Размеры нейрокраниума в этот контраст формы не входят.
Четвертый главный фактор противопоставляет биорбитальную ширину и ширину отдельных орбит поперечному развитию черепа, ширине его основания, высоте лица и носа, ширине неба. Дать сколько-нибудь ясную интерпретацию, имеющую анатомический смысл - затруднительно.
Варимакс-ротация позволила получить первый преобразованный фактор, который наиболее тесно связан с поперечными размерами черепа, преимущественно - нейрокраниума. Наибольшие нагрузки характерны для поперечного диаметра и ширины основания
- 142 -
Таблица 6.7 Результаты факторного анализа 20 размеров черепа
| Признаки | ||||
| Главные факторы | ||||
| 1.Продольный диаметр | 0.410 | -0.281 | -0.033 | 0.048 |
| 2.Поперечный диаметр | 0.513 | 0.480 | -0.110 | -0.255 |
| 3.Высота черепа от br | 0.194 | -0.071 | -0.067 | -0.007 |
| 4.Длина основания черепа | 0.226 | -0.225 | 0.081 | 0.076 |
| 5.Наименьший диаметр лба | 0.607 | 0.206 | 0.004 | -0.036 |
| 6.Наибольший диаметр лба | 0.459 | 0.416 | -0.190 | -0.159 |
| 7.Ширина основания черепа | 0.585 | 0.371 | -0.031 | -0.233 |
| 8.Ширина затылка | 0.432 | 0.162 | -0.158 | -0.070 |
| 9.Длина основания лица | 0.422 | -0.529 | 0.419 | -0.036 |
| 10.Верхняя ширина лица | 0.794 | 0.099 | 0.149 | 0.187 |
| 11.Биорбитальный диаметр | 0.782 | 0.111 | 0.068 | 0.606 |
| 12.Скуловой диаметр лица | 0.671 | 0.197 | -0.013 | -0.114 |
| 13.Средняя ширина лица | 0.579 | -0.122 | 0.140 | -0.171 |
| 14.Верхняя высота лица | 0.435 | -0.550 | -0.503 | -0.209 |
| 15.Ширина правой орбиты | 0.509 | -0.073 | -0.226 | 0.410 |
| 16.Высота правой орбиты | 0.187 | -0.151 | -0.492 | 0.165 |
| 17.Ширина носа | 0.383 | -0.039 | 0.374 | -0.094 |
| 18.Высота носа | 0.330 | -0.457 | -0.462 | -0.225 |
| 19.Длина неба | 0.366 | -0.442 | 0.291 | -0.059 |
| 20.Ширина неба | 0.371 | -0.110 | 0.391 | -0.244 |
| Доля вариации (%) Pi | 24.26 | 9.267 | 7.242 | 4.850 |
| Варимакс-факторы | ||||
| 1.Продольный диаметр | 0.090 | 0.312 | 0.303 | 0.230 |
| 2.Поперечный диаметр | 0.756 | -0.016 | 0.002 | 0.014 |
| 3.Высота черепа от br | 0.098 | 0.087 | 0.151 | 0.085 |
| 4.Длина основания черепа | -0.025 | 0.266 | 0.126 | 0.164 |
| 5.Наименьший диаметр лба | 0.554 | 0.203 | 0.064 | 0.243 |
| 6.Наибольший диаметр лба | 0.654 | -0.084 | 0.062 | 0.080 |
| 7.Ширина основания черепа | 0.718 | 0.123 | 0.027 | 0.061 |
| 8.Ширина затылка | 0.441 | 0.036 | 0.162 | 0.144 |
| 9.Длина основания лица | -0.084 | 0.768 | 0.144 | 0.130 |
| 10.Верхняя ширина лица | 0.516 | 0.403 | 0.033 | 0.517 |
| 11.Биорбитальный диаметр | 0.376 | 0.253 | -0.004 | 0.889 |
| 12.Скуловой диаметр лица | 0.623 | 0.242 | 0.118 | 0.203 |
| 13.Средняя ширина лица | 0.361 | 0.476 | 0.179 | 0.100 |
| 14.Верхняя высота лица | 0.090 | 0.195 | 0.861 | 0.043 |
| 15.Ширина правой орбиты | 0.182 | 0.052 | 0.275 | 0.610 |
| 16.Высота правой орбиты | 0.036 | -0.197 | 0.466 | 0.264 |
| 17.Ширина носа | 0.221 | 0.481 | -0.112 | 0.064 |
- 143 -
Таблица 6.7(Продолжение)
| Признаки | ||||
| 18.Высота носа | 0.077 | 0.126 | 0.748 | -0.021 |
| 19.Длина неба | -0.043 | 0.614 | 0.173 | 0.092 |
| 20.Ширина неба | 0.220 | 0.552 | -0.055 | -0.075 |
| Доля вариации (%) Pi | 15.61 | 11.78 | 9.379 | 8.849 |
черепа, а также - для наибольшего лобного диаметра. Несколько меньшие нагрузки проявляются для наименьшего диаметра лба, скулового диаметра и верхней высоты лица.
Второй варимакс-фактор описывает коррелированность признаков нижней лицевой зоны, особенно - верхнечелюстного отдела. Наибольшие нагрузки наблюдаются у длины основания лица и размеров неба. Меньшие значения нагрузок на этот фактор можно найти для ширины носа и средней ширины лица.
Третий варимакс-фактор описывает продольное развитие лица, имея наибольшие нагрузки на верхнюю его высоту и высоту грушевидного отверстия. Несколько меньшая нагрузка наблюдается для высоты орбиты. Наконец, четвертый фактор описывает поперечное развитие лица в зоне орбит. Здесь наибольшие нагрузки можно найти для биорбитального диаметра, ширины орбиты и верхней ширины лица.
Таким образом, вариации размера и формы черепа связаны с соотношениями четырех выделенных варимакс-ротацией групп признаков, описывающих:
1) поперечное развитие черепа, особенно - размеров нейрокраниума;
2) общее развитие верхнечелюстного отдела;
3) общее высотное развитие лица;
4) широтное развитие лица в орбитальной зоне.
Дата добавления: 2016-02-13; просмотров: 906;
