Другие техники факторного анализа
6.30 Все изложенное до сих пор в настоящей главе относится к так называемой R-технике факторного анализа. Вместе с тем, существуют другие такие техники: Q, P, O, S,
- 155 -
T, предназначенные для рассмотрения данных, которые получены при постановки других задач исследования. Эти различия заключаются в количестве рассматриваемых признаков, одно- или неоднократном их измерении, в способах нахождения коэффициентов корреляции. R-техника является основной, наиболее разработанной и часто используемой. Можно представить ситуации, когда задачи антропологических исследований будут такими, что применение иных техник факторного анализа окажется вполне уместным, а порой - и необходимым. В первую очередь это может касаться Q и T-техник.
6.31 В обычном, до сих пор рассматривавшемся случае, коэффициенты корреляции вычислялись по парам признаков для оценки тесноты связей между ними. Иными словами, они находились для сочетаний столбцов матрицы данных. Так, при рассмотрении, например, элементов 2-го и 3-го столбцов этой матрицы X можно было найти коэффициент корреляции r23 между признаками X2 и X3. При этом в вычислениях участвуют пары индивидуальных значений признаков X2i X3i у всех N наблюдений. Если в вычислениях участвуют все m признаков, в результате может быть получена обычная корреляционная матрица R набора признаков с размером m * m.

 X11 X21 X31 ... Xm1 ï
X11 X21 X31 ... Xm1 ï
X12 X22 X32 ... Xm2 rq13
X = X13 X23 X33 ... Xm3 ï
... ... ... ... ...
X1N X2N X3N ... XmN
ñ ñ
r23

 С логической точки зрения точно таким же образом можно прокоррелировать не столбцы, а - строки матрицы данных. В этой ситуации вычисления будут проводиться по парам значений всех m признаков у двух разных индивидов. Например, коррелируя 1-ю и 3-ю строки матрицы данных, мы получим коэффициент корреляции между 1-м и 3-м наблюдениями, который можно обозначить как rq13. Если в вычислениях примут участие все N строк, в результате будет получена корреляционная матрица
С логической точки зрения точно таким же образом можно прокоррелировать не столбцы, а - строки матрицы данных. В этой ситуации вычисления будут проводиться по парам значений всех m признаков у двух разных индивидов. Например, коррелируя 1-ю и 3-ю строки матрицы данных, мы получим коэффициент корреляции между 1-м и 3-м наблюдениями, который можно обозначить как rq13. Если в вычислениях примут участие все N строк, в результате будет получена корреляционная матрица
1 rq12 rq13 ... rq1N
rq12 1 rq23 ... rq2N
Rq = rq13 rq23 1 ... rq3N (6.75)
... ... ... ... ...
rq1N rq2N rq3N ... 1
для набора N наблюдений с размером N * N. Для того, чтобы отличать коэффициенты корреляции между признаками (rij) от аналогичных коэффициентов для наблюдений (rqij) будем пользоваться во втором случае подписным индексом q.
Обычный коэффициент корреляции между двумя признаками дает меру согласованности их вариации. Если увеличению (или уменьшению) в ряду наблюдений значений одного признака более или менее точно соответствует увеличение (или уменьшение) величины другого показателя, коэффициент корреляции между нами будет отличен от нуля. Аналогичным образом, коэффициент корреляции между двумя наблюдениями описывает согласованность у них значений признаков. Так, если эта корреляция положительна, то при увеличении какого-то признака у первого индивида, значение этого же признака
- 156 -
должно быть в какой-то мере увеличено и у второго наблюдения. Большая величина обычного коэффициента корреляции между двумя признаками ничего не говорит о сходстве абсолютных размеров этих признаков. Аналогичным образом, высокая корреляция, найденная для двух индивидов по набору признаков, не позволяет ничего сказать об их сходстве по абсолютным значениям этих признаков. Такая корреляция свидетельствует лишь о сходстве в соотношениях признаков.
Значения коэффициентов корреляции может изменяться от –1 до +1. Величина rqij = 1 означает полное сходство по соотношениям всех m признаков, при rqij = 0 любое такое сходство отсутствует, в случае rqij = -1 соотношения признаков у двух индивидов прямо противоположны.
6.32 При рассмотрении корреляционной матрицы R, найденной для набора m признаков, средствами факторного анализа, можно говорить о том, что применяется R-техника этого анализа. Аналогичное изучение корреляционной матрицы Rq, полученной для набора N индивидов, с использованием тех же самых приемов, называется применением Q-техники факторного анализа. В первом случае выделяются n факторов (n < m), каждый из которых должен учитывать взаимосвязи между признаками. Во второй ситуации находятся n факторов (n < N), описывающих взаимоотношения между индивидами. Факторные нагрузки, найденные в R-технике, и образующие в ортогональном случае матрицу факторного отображения A, позволяют сгруппировать признаки и указать какие сочетания их значений находятся на полюсах вариации факторов. Аналогичным образом, нагрузки на Q-факторы, позволяют сгруппировать индивидуальные наблюдения по степени сходства у них соотношений признаков.
Математическая специфика проведения Q-факторного анализа по сравнению с его R-техникой - относительно невелика. Так, здесь часто оказывается излишним проведение ротации факторных осей, так как полученные при первоначальной факторизации нагрузки группируют индивидуальные наблюдения, а эта группировка не изменяется при повороте факторов. Не всегда проводится и оценка значений факторов.
Таким образом, основная особенность Q-техники факторного анализа заключается в вычислении исходных корреляций. Обычно в статистических пакетах компьютерных программ коэффициенты корреляции получаются для столбцов матрицы данных, в каждом из которых находятся значения одного признака у N наблюдений. Эта проблема решается просто, так как оказывается достаточным транспонировать исходную таблицу данных, для чего в любом таком пакете программ имеется специальная команда. В результате в преобразованной матрице данных любой столбец будет содержать значения всех признаков у одного наблюдения. Иными словами, вычисление обычным образом корреляционной матрицы, но по предварительно транспонированной таблице данных, даст в качестве результата корреляционную матрицу Rq (6.75) связей между наблюдениями, и обычная ее факторизация будет соответствовать Q-технике факторного анализа. Таким образом, просто применяя к транспонированным данным стандартные для R-техники действия по проведению факторного анализа, можно получить результаты этого анализа для Q-техники.
Основной проблемой вычисления матрицы Rq является возможная несопоставимость единиц измерений разных признаков и присутствие сильных различий их абсолютной
- 157 -
величины. Поэтому, при вычислениях коэффициентов корреляции между любыми индивидами одни признаки всегда будут иметь только большие значения (для длины тела, например - 140 - 190 см), для других - средние (например, для акромиального диаметра - 32 - 43 см), для третьих - только малые (для жировых складок - 3 - 60 мм). Это приведет к тому, что все коэффициенты корреляции в матрице Rq будут очень близки к 1, что повлечет неудобства работы с ними. Для устранения такого эффекта можно нормировать значения всех признаков так, чтобы для каждого из них была бы характерна нулевая средняя и единичная дисперсия. Подобная нормировка легко реализуется в любом пакете статистических компьютерных программ. Важно, чтобы эта операция была бы проведена еще до транспонирования матрицы данных, так как нормировка осуществляется для столбцов матрицы данных (т.е. – для признаков).
Таблица 6.10 Результаты Q-факторного анализа 16 наблюдений по 22 размерам тела
| No наблю- дения | |||||||
| Ненормированные данные | Нормированные данные | ||||||
| 0.980 | -0.187 | -0.057 | -0.305 | -0.677 | 0.263 | ||
| 0.993 | 0.055 | -0.071 | 0.439 | -0.587 | 0.392 | ||
| 0.996 | -0.067 | -0.005 | 0.267 | -0.340 | -0.264 | ||
| 0.997 | 0.004 | 0.008 | 0.642 | 0.061 | 0.327 | ||
| 0.993 | 0.092 | -0.051 | 0.666 | -0.286 | -0.324 | ||
| 0.996 | 0.056 | -0.006 | -0.414 | 0.501 | 0.277 | ||
| 0.996 | 0.036 | 0.070 | -0.262 | 0.543 | -0.221 | ||
| 0.988 | 0.147 | 0.019 | 0.623 | 0.361 | 0.023 | ||
| 0.982 | 0.184 | 0.018 | 0.643 | 0.304 | -0.464 | ||
| 0.987 | -0.084 | 0.033 | -0.498 | -0.106 | 0.263 | ||
| 0.998 | -0.033 | -0.000 | -0.836 | 0.227 | 0.079 | ||
| 0.984 | -0.117 | 0.071 | 0.036 | 0.139 | 0.495 | ||
| 0.992 | 0.092 | 0.018 | 0.215 | 0.542 | 0.409 | ||
| 0.985 | -0.126 | 0.078 | -0.697 | 0.229 | -0.591 | ||
| 0.996 | 0.056 | -0.033 | -0.119 | -0.378 | -0.703 | ||
| 0.988 | -0.111 | -0.093 | -0.557 | -0.634 | 0.142 | ||
| Pi(%) | 98.16 | 1.077 | 0.243 | 25.369 | 17.149 | 13.743 |
Существует также рекомендация Имбри-Парди, в соответствии с которой факторизации следует подвергать специальный "показатель сходства пропорций" анализируемых объектов


 m m m 1/2
m m m 1/2
cos Qij = S xki xkj S xki2 S xkj2 . (6.76)
k = 1 k = 1 k = 1
- 158 -
Здесь xki и xkj - значения k-го признака у i-го и j-го наблюдения. Суммирования проводятся по всем m признакам. Это выражение имеет логический смысл коэффициента корреляции, так как в соответствии с формулой (6.43) cos Qij = rij. Поэтому, при использовании "показателя сходства пропорций" можно столкнуться с той же проблемой, что и при расчетах коэффициентов корреляции наблюдений по ненормированным данным.
Пример 6.8 Проиллюстрируем возможности Q-техники факторного анализа на модельном примере. В качестве исходных материалов использовались данные по 22 размерам тела у 16 женщин, выбранных с применением таблицы случайных чисел из общей их выборки 242 наблюдения. Исходная матрица корреляций между 16 наблюдениями вычислялась тремя способами: для ненормированных значений признаков, с применением показателя Имбри-Парди и для нормированных величин переменных. В первом случае, исходная таблица данных по 22 признакам у 16 наблюдений просто транспонировалась, после чего она подвергалась факторизации. Во второй ситуации матрица значений cos Qij получалась в соответствии с существующими рекомендациями (Йереског и др., 1980), а затем подвергалась факторизации. В третьем случае сначала проводилась нормировка каждого признака к стандартной форме варьирования с нулевой средней и единичной дисперсией, после чего проводилось транспонирование таблицы данных с последующим нахождением матрицы Rq и ее факторизацией.
Для первых двух случаев были получены матрицы, включавшие только очень большие коэффициенты, близкие к 1. Они изменялись от 0.93 до 0.99, в чем проявилось влияние различий в абсолютной величине признаков, среди которых были такие показатели как обхват груди и длина ноги - с одной стороны, и жировые складки - с другой. Для норми-рованных величин признаков корреляционная матрица включала различные коэффициенты, изменявшиеся от -0.60 до +0.62.
В каждом из трех случаев были выделены по три главных фактора. Результаты факторизации матриц корреляций между 16 индивидами, полученных по ненормированным данным и для показателя Имбри-Парди оказались практически идентичными и в таблице
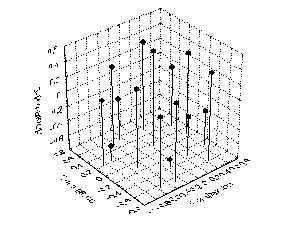
Рисунок 6.13. Размещение в пространстве первых трех факторов, найденных в Q-технике, 16 индивидуальных случаев в соответствии с их нагрузками
- 159 -
6.10 приведены только первые из них. Нетрудно видеть, что первый фактор описывает 98.2% суммарной вариации соотношений признаков у индивидов и имеет очень высокие нагрузки 0.98-0.99 у всех индивидуальных случаев. Никакой группировки наблюдений на его основе провести невозможно. Нагрузки на 2-м и 3-м факторах, напротив, практически для всех наблюдений очень близки к нулю. Таким образом, эффект различий абсолютной величины использованных признаков - налицо, и результаты Q-факторного анализа - неутешительны.
Совершенно иная картина была получена в ситуации, когда до проведения факторного анализа была осуществлена нормировка исходных значений признаков. Здесь (табл.6.10) первые три фактора описывают 56.3% суммарной вариации соотношений признаков у индивидов. Эти факторы по своим нагрузкам, имеющим самые разные величины и знаки, отчетливо разделяют 16 случаев.
На рисунке 6.13 можно видеть их размещение в пространстве первых трех факторов в соответствии с их нагрузками. Правда, в локализации этих индивидуальных точек трудно усмотреть какую-то структуру, что вполне естественно, так как здесь по существу представлен фрагмент непрерывной внутригрупповой межиндивидуальной вариабельности по соотношениям признаков.
6.33 Использование Q-техники факторного анализа для решения антропологических задач в первую очередь может быть приурочено к случаям рассмотрения межиндивидуальной вариации, содержащей некоторую структуру, обусловленную присутствием каких-то межгрупповых (межпопуляционных, таксономических и др.) явлений. Так, возможно применять этот способ анализа в исследованиях в области эволюционной антропологии, где актуальна проблема таксономической оценки отдельных индивидуальных находок. Вместе с тем, в следующем разделе нашего изложения будут рассмотрены многомерные методы, позволяющие решать эти проблемы гораздо более эффективно и с большей методической обоснованностью. По-видимому, Q-техника факторного анализа в приложении к антропологическим исследованиям является, все-таки - второстепенным инструментом.
6.34 Т-техника факторного анализа применяется к данным особого рода. Они характеризуются тем, что рассматривается только один признак X, измеренный у N индивидов, в несколько (m) моментов времени. Поэтому, матрица данных здесь имеет специальный вид. Каждый ее i-й столбец включает значения признака у всех индивидов в i-й момент времени, а каждая j-я строка содержит многократно измеренные значения этого признака у j-го индивида. Такие данные могут быть получены при решении специальных задач. Во-первых, можно представить себе, что рассматриваемый признак отличается определенной неустойчивостью своего индивидуального уровня, испытывая колебания в течение относительно коротких промежутков времени, иногда даже нескольких часов. С подобным явлением, например, можно столкнуться при изучении некоторых физиологических показателей. Тогда рассмотрение такой динамики у разных индивидов может позволить установить степень стабильности признака, закономерности его изменений и вызывающие их причины.
- 160 -
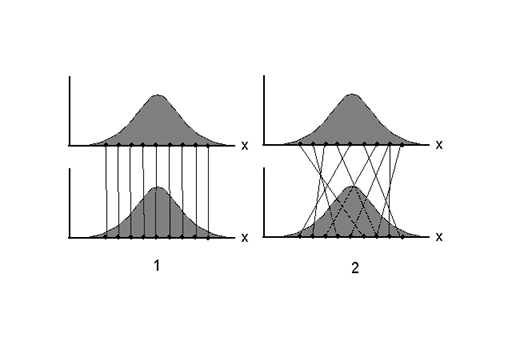
Рисунок 6.14. К истолкованию смысла коэффициента корреляции между двумя распределениями признака: 1 - случай высокой связи 2 - случай слабой связи
Второй круг задач антропологических исследований, приводящих к необходимости применения T-техники факторного анализа, связан с проведением продольных исследований роста и развития у детей и подростков. Здесь также имеются несколько моментов времени, разделенных обычно годовыми интервалами, для каждого из которых имеется распределение значений рассматриваемого признака у одних и тех же индивидов.
Наконец, аналогичная структура данных возникает при неоднократном изучении одного и того же набора групп населения в разные моменты времени, разделенные иногда десятилетиями. При этом можно интересоваться преемственностью основных межгруп-повых закономерностей вариации средних значений признака. Большая или меньшая устойчивость межгруппового распределения признака и причины его стабильности или динамичности представляют значительный научный интерес. По-видимому, вопрос о преемственности межгруппового распределения признаков возникает в практике антрополо-гических исследований чаще, чем это кажется на первый взгляд. При сборе антропологического материала по взрослым контингентам возрастной интервал выбирается обычно от 18 - 20 до 50 - 60 лет. В случае достаточного объема выборки его можно разделить на несколько отрезков в 5 - 10 лет. В результате можно получить 4 - 8 межгрупповых распределений признака, каждое из которых будет включать средние величины, найденные для нескольких групп населения применительно к определенному узкому возрастному интервалу.
6.35 Таким образом, если мы имеем m возрастных или временных срезов, которым соответствуют m распределений значений некоторого признака, то для описания сходства или различий закономерностей вариации, проявляющихся в этих распределениях, следу-
- 161 -
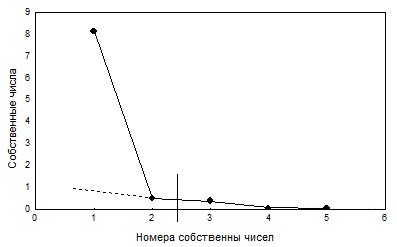
Рисунок 6.15 График собственных значений, полученных при проведении T-факторного анализа длины тела в 10 возрастных группах мальчиков
ет вычислить коэффициенты корреляции между ними. Смысл этих корреляций иллюст-рирует рисунок 6.14. Очевидно, в случае высокой стабильности структуры этого распределения за некоторый момент времени каждое наблюдение сохранит в нем свое место. Напротив, низкая стабильность приведет к тому, что со временем расположение разных случаев в распределении может значительно измениться.
Для всех m распределений можно найти корреляционную матрицу, факторизация которой стандартными средствами R-техники факторного анализа будет равносильна проведению T-факторного анализа. Если для распределений значения признака наблюдается стабильность, корреляционная матрица будет включать значительные коэффициенты корреляции, которые проявятся в первом факторе. В этом случае он будет иметь генеральный характер с высокими нагрузками на все временные точки и опишет, таким образом, стабильность структуры распределения признака со временем. Доля учитывае-мой им изменчивости признака может служить мерой стабильности вариации этого показателя в разные моменты времени. Второй и последующие факторы в силу их биполярности отразят наличие явлений динамики структуры распределений признака.
Проведение T-факторного анализа не имеет существенных особенностей по сравне-нию с его R-техникой. Исходная матрица данных в качестве строк должна включать m значений признака в разные моменты времени у некоторого индивида. Столбцами этой матрицы являются значения признака у всех индивидов, измеренные в определенный момент времени. Такая матрица может рассматриваться стандартными средствами фак-торного анализа, что будет соответствовать T-технике. При проведении такого рассмот-рения обычно ограничиваются получением ортогонального факторного отображения в ходе первичной факторизации.
Пример 6.9 Выполним T-факторный анализ данных продольных наблюдений над мальчиками г. Москвы 8 - 17 лет, проведенные В.Г.Властовским. Рассматривалась длина тела у 148 индивидов. При выделении главных факторов было найдено 5 собственных чисел,
- 162 -
Таблица 6.11 Результаты Т-факторного анализа распределения длины тела у мальчиков 8 - 17 лет
| Возрастные группы | ||
| 8 лет | 0.932 | 0.023 |
| 9 лет | 0.934 | 0.017 |
| 10 лет | 0.968 | 0.009 |
| 11 лет | 0.971 | 0.056 |
| 12 лет | 0.959 | 0.199 |
| 13 лет | 0.939 | 0.288 |
| 14 лет | 0.931 | 0.222 |
| 15 лет | 0.802 | -0.036 |
| 16 лет | 0.927 | -0.318 |
| 17 лет | 0.838 | -0.441 |
| Доля вариации (%) Pi | 81.24 | 4.81 |
график которых (рис.6.15) демонстрирует начало пологого и примерно прямолинейного участка, начиная со второго из них. Поэтому, в соответствии с критерием отсеивания Кеттела следует рассматривать только первые два фактора, которые суммарно описывают 86.1% суммарной вариации длины тела в 10 возрастных группах мальчиков.
Первый T-фактор (табл.6.11) имеет генеральный характер, так как его нагрузки на все возрастные группы положительны и довольно велики. Он отражает стабильность распределения длины тела в разных возрастных точках. Его факторная доля изменчивости имеет весьма большую величину (81.2%), и можно сказать, что возрастная стабильность структуры распределения длины тела у мальчиков 8 - 17 лет очень велика.
Второй полученный фактор - биполярен и выделяет, таким образом, две совокупности возрастных точек (рис.6.15). Первую из них образуют возрастные группы мальчиков от 12 до 14 лет - т.е. относящиеся к первой половине пубертатного периода. Для них характерны положительные нагрузки. Для возрастного периода 15 - 17 лет эти нагрузки становятся отрицательными. Годовые группы 8 - 11 лет имеют практически нулевые нагрузки на второй фактор.
Таким образом, этот фактор описывает две фазы изменений структуры распределения длины тела. Первая из них происходит в начале и середине пубертатного периода, вторая - в его конце. Они связаны с тем, что вследствие вариации биологического возраста, про-являющейся в любой хронологически однородной группе детей, некоторые акцелери-рованные индивиды рано вступают в фазу ускоренного роста, что приводит к некоторым изменениям структуры распределения длины тела в возрасте 12 - 14 лет. Эти процессы проявляются в отчетливых изменениях нагрузок второго фактора в этом возрасте (рис. 6.16). В дальнейшем в конце пубертатного периода акцелерированные дети несколько раньше завершают свой рост, по сравнению со своими ретардированными сверстниками, которые, находясь в стадии быстрого подросткового роста, наверстывают свое отставание и значительно изменяют свое место во внутригруппом распределении. Это приводит ко второй и финальной перестройке структуры распределения, проявлением чего оказываются изменение нагрузок на возрастные точки 15 - 17 лет.
- 163 -
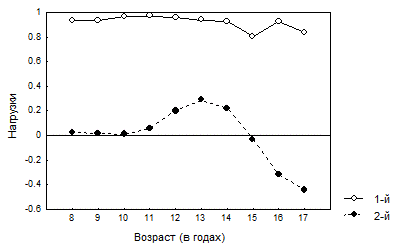
Рисунок 6.16 График нагрузок на первые два фактора при проведении T-факторного анализа длины тела в 10 возрастных группах мальчиков
Вместе с тем, второй фактор учитывает всего 4.8% суммарной вариации длины тела в разных возрастных группах мальчиков, и можно сказать, что основным явлением, которое можно обнаружить в рассматриваемых данных, оказывается относительная стабильность распределения индивидуальных значений длины тела, описываемая первым Т-фактором.
6.36 Простейшее изложение факторного анализа можно найти в книгах Я.Окуня (1974), Г.В.Суходольского (1972) и Дж.Девиса (1977). Наиболее подробно факторный анализ изложен в руководствах Д.Лоули и А.Максвелла (1967), Г.Хармана (1972), К.Иберлы (1980) , К.Г.Йерескога и др. (1980). Следует также упомянуть книги В.М.Жуковской и И.Б.Мучник (1976), В.Плюты (1980), сборник "Статистические методы для ЭВМ" (1986), книги Дж.Кима и др.(1989), С.А.Айвазяна и др. (1989), учебные пособия "Компьютерная биометрика" (1990) и А.М.Дуброва и др. (1998).
Дата добавления: 2016-02-13; просмотров: 957;
