Характеристичні функції

Дуже важливими для практики є характеристичні функції, вони дають певні фізичні величини, які можуть бути виміряні на практиці. Всі термодинамічні потенціали при природних умовах є характеристичними функціями. Так їх називають тому, що за величиною самої функції та її похідних можна просто і в явному вигляді представити всі термодинамічні властивості системи. Аналогічно, при v = const і Т = const характеристичною функцією буде вільна енергія Гельмгольца, а при р = const і Т = const – потенціал Гіббса.

Розглянемо деякі термодинамічні співвідношення. Розглянемо вільну енергію Гіббса:

G = H – TS. (2.43)

Диференціюємо

dG = dH – TdS – SdT. (2.44)

З рівняння (2.8)

dG = dU +pdv + vdp – TdS – SdT. (2.45)

З рівняння (2.5)

dG = dq + vdp – TdS – SdT. (2.46)

Оскільки dS =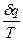

dG = vdp – SdT. (2.47)

Розділемо на dp, при постійній температурі, матимемо

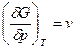. (2.48)

Можна отримати і інші співвідношення, наприклад

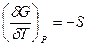(2.49)

та

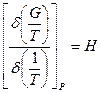. (2.50)

Підсумуємо

Функції стану системи – U, H, S, F, G.

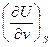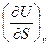U dU = TdS – pdv = –р, = T

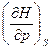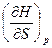H = U + pv dH = TdS + vdp = v, = T

S dS = dU/T = (C_v/T) dT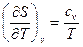

dS = dH/T = (C_p/T) dT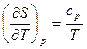

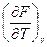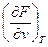F = U – TS dF = -SdT – pdv = –S, = –p

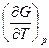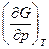G = U – TS + pv = H – TS dG = -SdT + vdp = –S, = v

Беручи різні похідні, можна отримувати значення фізичних властивостей, які представляють інтерес для фахівців, що не займаються діаграмами стану.

Наприклад, без виводу, коефіцієнт розширення

a = 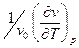(2.51)

Коефіцієнт стискуваності

b = 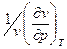(2.52)

Подібних формул дуже багато. Існують навіть таблиці, з яких можна взяти інформацію, якій властивості дорівнюють які похідні.