Формулювання другого закону термодинаміки
1. Вічний двигун другого роду неможливий.
2. Вперше висловлено М.В.Ломоносовим, а в 1850 р. сформульовано Рудольфом Юліусом Емануелем Клаузіусом:теплота не може самовільно переходити від холодного тіла до гарячого. Або неможливо здійснити такий процес, єдиним результатом якого був би перехід тепла від холодного тіла до більш гарячого.
3. За Кельвіном: не існує циклічного процесу, єдиним результатом якого було б поглинання системою теплоти з оточуючого середовища і виконання еквівалентної роботи.
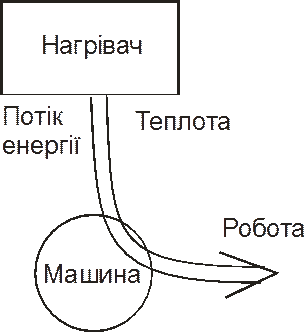
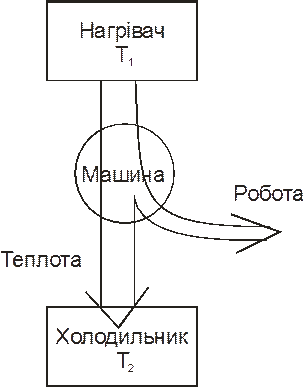
Щоб отримати роботу з теплової енергії частина її має бути витрачена марно і віддана резервуару теплоти з нижчою температурою (рис. 2.4). В термодинаміці для спрощення резервуар з вищою температурою називають нагрівачем, з нижчою – холодильником.
| 
|
| Вічний двигун 2-го роду | Реальна машина |
Рис. 2.4. Вічний двигун 2-го роду і теплова машина.
Уявімо собі металічний дріт. Частина електронів в кристалічній гратці цього металу локалізована – пов’язана з атомами у вузлах гратки, частина – утворює електронний газ і рухається хаотично. Прикладемо різницю потенціалів. Вільні електрони починають рухатися в одному напрямку, утворюючи електричний струм, тобто виконуючи роботу. Знімемо напругу. Електрони знов почали рухатися хаотично. Їх довільний рух хаотичний. Загалом, усі самочинні процеси, які відбуваються в системі, підвищують в ній хаос.
Ми вже знаємо, що з двох характеристик системи, які утворюють її внутрішню енергію – теплоти і роботи – за хаотичний рух відповідає теплота, за спрямований – робота. Отже, нас далі буде цікавити теплота.
Візьмемо газ як ізольовану систему. Молекули газу рухаються хаотично. При чому, чим вище температура газу, тобто чим більшу теплоту він має, тим хаотичніший рух молекул. При зниженні температури (відбиранні теплоти) швидкість руху молекул зменшується, частота їх стикань менше, рух менш хаотичний. При ще нижчій температурі і відтак, кількості теплоти, газ перетворюється на рідину, де можливості хаотичного руху молекул значно обмежені порівняно із газом. І так далі. В твердому тілі молекули лише коливаються навколо своїх позицій в кристалі, а при абсолютному нулі завмирають.
Отже, пов’язані між собою температура і теплота визначають ступінь хаотичності в системі. Величину 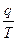 називають наведеною теплотою або ентропією S. Ця функція була введена Клаузіусом.При термодинамічному розгляді ентропії розглядають її зміну при хімічній реакції або фізичному перетворенні, глибина протікання яких залежить від енергії, переданої у вигляді теплоти, адже робота, пов’язана із впорядкованим рухом, на ентропію не впливає.
називають наведеною теплотою або ентропією S. Ця функція була введена Клаузіусом.При термодинамічному розгляді ентропії розглядають її зміну при хімічній реакції або фізичному перетворенні, глибина протікання яких залежить від енергії, переданої у вигляді теплоти, адже робота, пов’язана із впорядкованим рухом, на ентропію не впливає.
Нехай система знаходиться в стані 1 і має ентропію S1 = 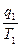 . Потім система перейшла в стан 2 з ентропією S2 =
. Потім система перейшла в стан 2 з ентропією S2 = 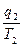 . Зміну ентропії можна записати як:
. Зміну ентропії можна записати як:
S2 – S1 = 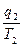 –
– 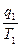 . (2.27)
. (2.27)
Якщо після цього вона повернулася в стан 1, тобто зробила коловий процес, то загальна зміна ентропії дорівнюватиме 0. Отже, для циклу можна записати:
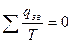 , (2.28)
, (2.28)
де Т – температура, при якій відбувається передача теплоти. Для нескінченної кількості елементарних циклів – циклів Карно – можна записати:
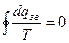 . (2.29)
. (2.29)
Підінтегральна величина представляє собою повний диференціал однозначної функції стану. Кожна система в будь-якому стані має певне і єдине значення ентропії, так само як Р, Т, U та інших властивостей. Ентропія є екстенсивною величиною. Тобто, вона ділиться на два, коли система розділяється на дві частини. Аналогічно, внутрішня енергія та об'єм є екстенсивними величинами, тоді як тиск є інтенсивною величиною.
Отже, ентропія визначається рівнянням
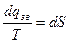 . (2.30)
. (2.30)
Цей вираз є аналітичним виразом другого закону термодинаміки для зворотних процесів. Для кінцевої зміни системи від стану 1 до стану 2 можна записати
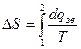 . (2.31)
. (2.31)
Щоб дати фіксовану точку відліку, ентропія чистої речовини при 0 К приймається рівною нулю (теорема Нернста, або третій закон термодинаміки). Ентропія при Т К тоді дорівнює
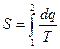 . (2.32)
. (2.32)
Бачимо, що ентропія обернено залежить від температури. Це означає, що при передачі однакової кількості теплоти холодному і гарячому тілам зміна ентропії буде різною. Приклад – кашель в тихій бібліотеці дуже чутний, а на гучній вулиці непомітний.
Розмірність ентропії 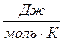 – така само, як для універсальної газової сталої R і теплоємності сV, cp.
– така само, як для універсальної газової сталої R і теплоємності сV, cp.
Оскільки, як ми знаємо з І закону, q = H, зміну ентропії при будь-якому перетворенні можна записати як:
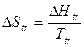 . (2.33)
. (2.33)
Але dH = cpdT. (2.34)
Тоді S = 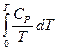 (2.35)
(2.35)
Емпірично встановлені два правила, важливі для металургії.
1. Правило Річардса. Зміна ентропії при плавленні 1 моля простих металів з однаковою кристалічною структурою і близькою структурою розплавів приблизно однакова і становить 8-16 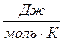 .
.
2. Правило Трутона. Зміна ентропії при випаровування 1 моля розплаву приблизно однакова і становить 88 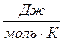 .
.
Бачимо, що зміна ентропії при випаровуванні значно більша, ніж при плавленні. Дійсно, в газах набагато більше хаосу, ніж в рідинах.
Якщо перший закон приводить до висновку, що внутрішня енергія є однозначною функцією стану системи, то другий закон – що ентропія також є функцією стану системи. Важливо пам’ятати, що аналітичний вираз першого закону термодинаміки слушний як для зворотних, так і для незворотних процесів, a вираз (2.30) – лише для зворотних. Зворотний перехід тепла можливий у тому випадку, коли температура теплоприймача на нескінченно малу величину менша за температуру теплового резервуару, що втрачає тепло, тобто різниця цих двох температур прямує до нуля. Термін "зворотний" означає, що при даних умовах напрямок переходу тепла може бути змінено на зворотний нескінченно малою зміною температури двох тіл. Зворотний перехід тепла є ідеалізованим процесом, але у принципі він є можливим.
Подивимося тепер, як змінюється ентропія у незворотних процесах. Нехай система переходить зі стану 1 в стан 2 двома шляхами – зворотно і незворотно. Запишемо для цих процесів перший закон термодинаміки:
qзв = DUзв + Азв, (2.36)
qнезв = DUнезв + Анезв, (2.37)
DUзв = DUнезв, адже початковий і кінцевий стани однакові.
З першого закону термодинаміки ми знаємо, що робота зворотного процесу максимальна. Тоді
qзв - qнезв = Азв, - Анезв, >0. (2.38)
Відтак, поглинена системою теплота у зворотному процесі більша, ніж у незворотному. Або віддана системою теплота при незворотному процесі більша, ніж при зворотному. Оскільки DS в обох процесах однакова (адже S – функція стану), то
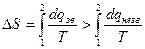 або
або 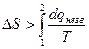 . (2.39)
. (2.39)
При зворотному адіабатному процесі dq = 0 i DS = 0. При незворотному адіабатному процесі DS > 0. Отже, для незворотних процесів рівняння другого закону термодинаміки переходить у нерівність
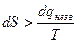 . (2.40)
. (2.40)
В загальному вигляді – для зворотних і незворотних процесів закон можна записати як
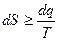 . (2.41)
. (2.41)
Цей вираз називають нерівністю Клаузіуса.
Підіб'ємо підсумок:
| Процес | Система | dS – зміна ентропії системи |
| Ізольована | Неізольована | |
| Зворотний | dS = 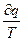 = 0 = 0
| dS = 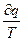
|
| Незворотний | dS > 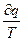 > 0 > 0
| dS > 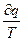
|
В ізольованій системі при зворотних процесах dS = 0 (нема теплообміну dq = 0). Це означає, що ентропія в стані рівноваги, коли можливі лише зворотні процеси, максимальна. Якщо ізольована система нерівноважна, і в ній йдуть незворотні процеси, dS > 0. Це означає, що в нерівноважній ізольованій системі всі процеси проходять із зростанням ентропії. В ізольованій системі неможливі процеси, при яких ентропія зменшується (dS < 0). В неізольованій системі це можливо.
Дата добавления: 2016-02-27; просмотров: 1287;
