Если ошибки измерений подчинены нормальному закону распределения, то метод МП сводится к методу НК.

Доказано, что получается при этом оценки - оптимальные !

То есть МНК оценки - эффективные !! ( в классе линейных оценок )

Однако Гаусс понимал, что нормальность не всегда имеет место, и поэтому подчеркивал, что основным доводом, которым он руководствовался, вводя этот метод, является вычислительная простота.

На самом деле “Нормальность - это миф. В реальном мире никогда не было и никогда не будет нормального распределения”.

“Каждый уверен в справедливости закона ошибок, экспериментаторы - потому, что они думают, что это математическая теорема, математики - потому, что они думают, что это экспериментальный факт”.

В действительности распределения часто являются «приближенно нормальными».

Поэтому еще в 1805 году Лежандр указывал, что прежде, чем воспользоваться этим методом ( и, в частности, выборочным средним ), следует тщательно просмотреть выборку и отбросить те выборочные значения, которые являются или кажутся аномальными ( то есть провести редактирование выборки ). В 1818 году Бессель при исследовании ряда выборок большой длины пришел к выводу, что большие значения ошибок измерений встречаются несколько чаще, чем это было бы при нормальном законе распределения ошибок.

В настоящее время общепринятым является утверждение, что 1-10% аномальных значений в общей массе данных - это скорее правило, а не исключение.

Пример: требуется оценить параметр сдвига ( меру положения ) 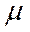для

выборки x₁, x₂,..,x_n. МНК приводит к задаче минимизации выражения 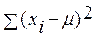и оценка математического ожидания дается в виде среднего арифметического 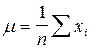. Эта

оценка является эффективной в случае нормально

распределенных случайных величин.

Теперь рассмотрим набор данных:

0.96; 1.01; 0.97; 1.02; 1.04; 1.00; 10.52

МНК: 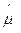₁ = 2.36

Если отбросить последние значение (10.52), то получится 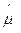₂ = 1 !