Введение в помехоустойчивое оценивание
В 1818 году Лаплас предложил метод наименьших модулей для решения задачи линейной регрессии с одним параметром ( наклон ) при произвольном симметричном распределении ошибок измерений.
f(xi, Q) = 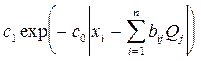
При этом функцию правдоподобия составить можно gn(x \ Q) = 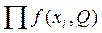 , а уравнение правдоподобия записать нельзя вследствие неаналитического характера функции ( нет производной, так как модуль - негладкая функция ). Поэтому для получения максимально правдоподобных оценок необходимо искать минимум функции Ln(x \ Q) =
, а уравнение правдоподобия записать нельзя вследствие неаналитического характера функции ( нет производной, так как модуль - негладкая функция ). Поэтому для получения максимально правдоподобных оценок необходимо искать минимум функции Ln(x \ Q) = 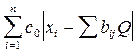 непосредственно.
непосредственно.
Решение дает оценку 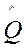 , равную медиане выборки.
, равную медиане выборки.
Медиана - значение X, при котором функция распределения Ф(x) = 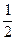 . Если выборку упорядочить по возрастанию, то медиана - значение среднего элемента выборки.
. Если выборку упорядочить по возрастанию, то медиана - значение среднего элемента выборки.
В предыдущем примере:
0.96; 0.97; 1.00; 1.01; 1.02; 1.04; 10.52
1 2 3 4 5 6 7
медиана дает оценку 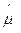 = 1.01, то есть вполне приемлемый результат.
= 1.01, то есть вполне приемлемый результат.
Робастные оценки
Реальные ряды ошибок измерений достаточно хорошо описываются распределениями с тяжелыми хвостами или 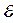 - загрязненными распределениями.
- загрязненными распределениями.
Пусть измерительное устройство с вероятностью (1 - 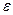 ) работает в основном режиме, при котором ошибка измерений имеет распределение P0(z) с дисперсией
) работает в основном режиме, при котором ошибка измерений имеет распределение P0(z) с дисперсией 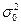 , и с небольшой вероятностью
, и с небольшой вероятностью 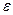 - в режиме «сбоев», при котором ошибка распределена по закону H(z) c дисперсией
- в режиме «сбоев», при котором ошибка распределена по закону H(z) c дисперсией 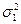 . Тогда общее распределение ошибок имеет вид
. Тогда общее распределение ошибок имеет вид
P(z) = 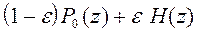 ,
,
а дисперсия выборочного среднего M 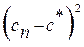 , где Сn -выборочное средние, равна
, где Сn -выборочное средние, равна 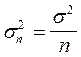 , где
, где 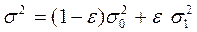 .
.
При 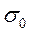 =1,
=1, 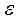 = 0.1,
= 0.1, 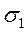 = 3 имеем
= 3 имеем 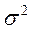 = 1.8, а при
= 1.8, а при  = 5,
= 5, 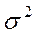 = 3.4.
= 3.4.
Таким образом, дисперсия выборочного среднего 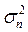 быстро растет с увеличением дисперсии
быстро растет с увеличением дисперсии 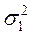 , а при
, а при  ( когда H - распределение Коши ) выборочное среднее становится несостоятельной оценкой параметра c*( то есть не сходится по вероятности к c*).
( когда H - распределение Коши ) выборочное среднее становится несостоятельной оценкой параметра c*( то есть не сходится по вероятности к c*).
Задача теории робастного оценивания:
Найти такие оценки параметров, которые были бы нечувствительными к отклонениям ошибок от нормального закона ( наличие выбросов и так далее ), но не слишком бы проигрывали в эффективности по сравнению с оценками МП, если закон распределения ошибок - нормальный.
Считается, что потери 5-10% эффективности - вполне приемлемая плата за устойчивость оценок. Наиболее удачным считается метод помехоустойчивого оценивания, основанный на приеме максимального правдоподобия - M-оценки.
М - оценки
Пусть x1, x2,..,xn- последовательность независимых, одинаково распределенных случайных величин, имеющих непрерывную плотность вероятности f(x - Q), где Q - параметр сдвига. Логарифм функции правдоподобия можно записать
lоg(Q) = L(Q) =  , где p(x) = -lоf(x)
, где p(x) = -lоf(x)
Согласно методу МП требуется максимизировать lоg(Q)или, что то же самое, минимизировать K(Q) =  .
.
Предположим, что минимум можно найти путем дифференцирования и решения уравнения K  (Q) = 0, то есть поиском соответствующего значения параметра сдвига Q, которое удовлетворяет условию
(Q) = 0, то есть поиском соответствующего значения параметра сдвига Q, которое удовлетворяет условию
(*)  , где
, где 
Решение этого уравнения, минимизирующее K(Q) называется оценкой максимального правдоподобия или М - оценкой параметра Q и обозначается 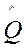
Приведем учебные примеры распределения погрешностей и соответствующие им оценки максимального правдоподобия:
1. нормальное распределение
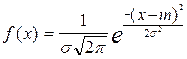 , при m = 0 и
, при m = 0 и 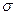 =1
=1 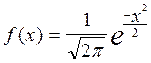
p = -lnf(x) = 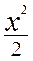 ;
; 
Уравнение (*) имеет вид  и дает оценку
и дает оценку 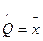
2. двойное экспоненциальное распределение
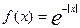 ; p = -lnf(x) = | x |
; p = -lnf(x) = | x |
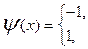

Уравнение (*) имеет вид 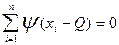 дает оценку
дает оценку  , равную медиане.
, равную медиане.
Хьюбер, используя строгое определение помехоустойчивости, нашел общий вид функций:
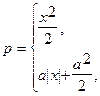
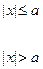
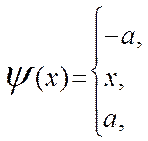
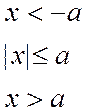
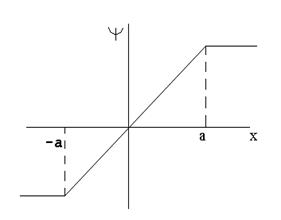
Эти функции минимизируют асимптотическую дисперсию V(T) оценок, где T- класс точности.
Использование этих функций приводит к следующим оценкам параметров сдвига:
1. 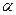 - усеченные оценки.
- усеченные оценки.
Исходная выборка упорядочивается: y(1) 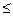 y(2)
y(2) 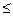 ...
... 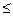 y(n)
y(n)
Отбрасывается 100% 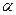 ( 0<
( 0< 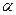
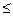 0.5 ) минимальных порядковых статистик (членов выборки) и 100%
0.5 ) минимальных порядковых статистик (членов выборки) и 100% 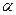 максимальных порядковых статистик. По оставшимся элементам берется выборочное среднее. Полученная таким способом оценка называется
максимальных порядковых статистик. По оставшимся элементам берется выборочное среднее. Полученная таким способом оценка называется 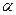 - усеченным средним и имеет вид:
- усеченным средним и имеет вид:
Ct( 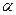 ,n) =
,n) = 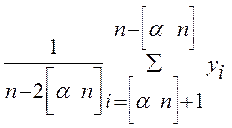
2. 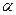 - винзорированные оценки
- винзорированные оценки
Введены в начале 40-х годов К.П. Винзором
[ 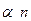 ] крайних значений не отбрасываются, проектируются в ближайшую точку оставшейся части упорядоченной выборки
] крайних значений не отбрасываются, проектируются в ближайшую точку оставшейся части упорядоченной выборки
Cw ( 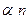 ) =
) = 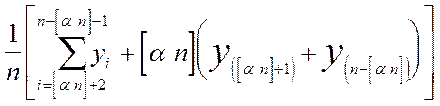
Дата добавления: 2016-02-20; просмотров: 815;
