Проверка гипотез для дисперсий.

Проверить, отличается ли выборочная дисперсия от стандартной , заранее известной – ( 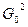) можно, используя 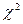распределение, которому подчиняется выборочная дисперсия.

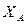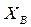Для двух случайных величин и проверка выборочных дисперсий проводится с помощью F-распределения. При этом можно пользоваться следующей таблицей:

Гипотеза	Используемый критерий	Число степеней свободы	Решение	Замечания
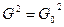
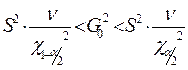
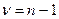
			Гипотеза принимается, если неравенства справедливы	Двусторонний критерий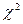
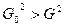
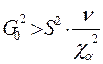
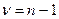
			Гипотеза принимается, если неравенства справедливы	Односторонний критерий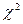
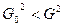
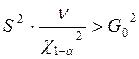
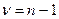
			Гипотеза принимается, если неравенства справедливы	Односторонний критерий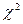
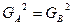
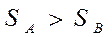
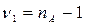
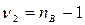
			Гипотеза принимается, если неравенства справедливы	Двусторонний критерий F. Проверять нужно только правое ограничение, так как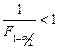
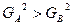
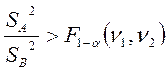
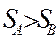
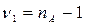
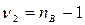
			Гипотеза принимается, если неравенства справедливы	Двусторонний критерий F.

Для примера рассмотрим критерий F из четвёртой строки. Проверяем гипотезу ; ® . Так как всегда <1, проверяем только правое неравенство, то есть .

Пример. Смонтированы две опытные установки.

Получены результаты

	Установка А (кг)	Установка В (кг)
	97, 8 98, 9 101, 2 98, 8 102, 0 99, 0 99, 1 100, 8 100, 9 100, 5	97, 2 100, 5 98, 2 98, 3 97, 5 99, 9 97, 9 96, 8 97, 4 97, 2
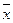
	99, 9	98, 1
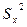
	1, 69	1, 44

Проверить равенство дисперсий Н₀: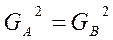

.

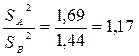При находим .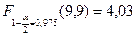

1, 17<4, 03.

Гипотеза принимается.

Отличие дисперсий незначимо.