Опыты независимы !!

g(Q₁, Q₂ \ x₁, x₂,..,x_n ) =

=

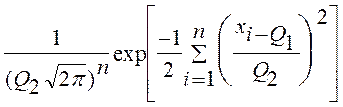
(***) lng = L =-nln(Q₂ ) -

(****)

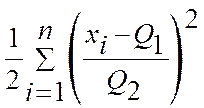
Решение системы (****) дает следующие оценки:

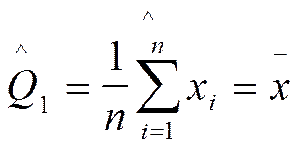
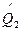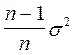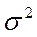E[ ] = , где - дисперсия - параметр закона распределения

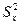- выборочная дисперсия - несмещенная оценка дисперсии

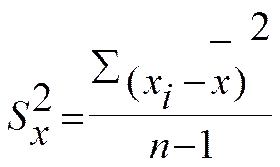
- смещенная оценка параметра 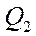- дисперсии

В (***) первый член не влияет на положение максимума, так как 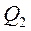- параметр масштаба, а не сдвига. Второй же член входит в L со знаком ( - ). Поэтому для максимизации функции правдоподобия необходимо минимизировать выражение 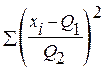, то есть сумму квадратов отклонений случайных величин от своего математического ожидания ( от среднего ). Это обстоятельство, по существу, - теоретическое обоснование метода наименьших квадратов.

МНК был разработан К. Гауссом в начале 19 века. Основное его достоинство - простота реализации и ясный физический смысл. МНК широко применяется в различных задачах, связанных с построением математических моделей. Параметры моделей подбираются таким образом, чтобы минимизировать сумму квадратов отклонений вычисленных по модели значений от наблюденных, и так далее ( такая же задача ставится при обработке измерений ).