Системы случайных величин
Функции распределения случайных величин
F(x, y) = P((X < x)(Y < y))
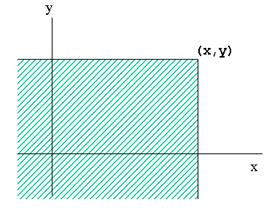
Плотность распределения вероятностей случайных величин
f(x, y) = 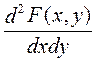 -элементарные вероятности
-элементарные вероятности
P((X,Y) 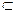 D) =
D) = 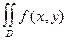 dxdy
dxdy
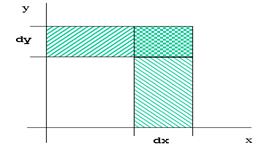
Геометрически вероятность попадания в область D изображается объемом цилиндрического тела С, ограниченного сверху поверхностью распределения и
опирающеюся на область D.
Свойства плотности распределения двух величин:
f(x,y) 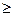 0
0
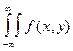 dxdy = 1
dxdy = 1
F1(x)=F 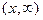 =
= 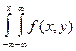 dxdy
dxdy
f1(x) = F 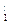 (x) =
(x) = 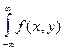 dy
dy
f2(y) = F 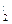 (y) =
(y) = 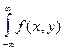 dx
dx
f(x,y) dxdy = P[(x < X < x + dx)(y < Y < y + dy)]
Условная плотность вероятности - f(x\y)
f(x\y) = 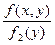 =
= 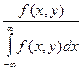
f(y\x) = 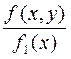 =
= 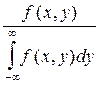 ,
,
то есть f(x,y) = f(x)f(y\x)
! Для независимых случайных величин f(x,y) = f(x)f(y)
Числовые характеристики системы двух случайных величин
1. Начальный момент порядка k,s
ak,s = M[xk ys]
2. Центральный момент порядка k,s
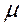 k,s = M[
k,s = M[ 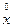 k
k 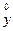 s] ;
s] ; 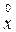 = x - mx
= x - mx
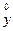 = y - my
= y - my
то есть ak,s = 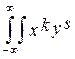 f(x,y) dxdy
f(x,y) dxdy
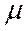 k,s =
k,s = 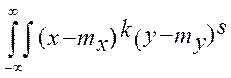 f(x,y) dxdy
f(x,y) dxdy
Первые начальные моменты
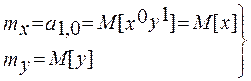 -координаты средней точки
-координаты средней точки
Вторые центральные моменты - дисперсии 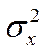 и
и 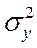
Dx = 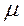 2,0 = M[
2,0 = M[ 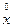 2
2 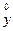 0] = M[
0] = M[ 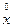 2] = D[x]
2] = D[x]
Dy = 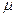 0,2 = D[y]
0,2 = D[y]
Второй смешанный центральный момент - корреляционный момент
kks = M[ 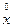
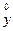 ] = M[(x-mx)(y-my)]
] = M[(x-mx)(y-my)]
kks = 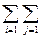 (xi - mx) (yj - my) Pij
(xi - mx) (yj - my) Pij
Rxy = 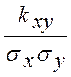 -коэффициент корреляции ( безразмерная величина )
-коэффициент корреляции ( безразмерная величина )
Дата добавления: 2016-02-20; просмотров: 616;
