Функция распределения вероятностей
Функцию распределения вероятностей определяют как вероятность события, заключающегося в том, что наблюдаемая величина X меньше или равна допустимому ее значению x, то есть
Fx(x) = P (X 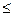 x)
x)
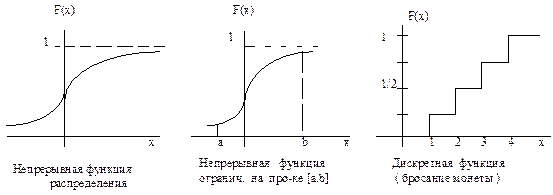
1) 0 £ Fx(x) £ 1 - 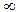 < x <
< x < 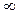
2) Fx(- 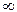 ) = 0 ; Fx(
) = 0 ; Fx( 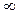 ) = 1 ;
) = 1 ;
3) Fx(x2) > Fx(x1) при x2 > x1
4) P(x1 < x £ x2) = F(x2) - F(x1)
Плотность распределения вероятности
- Производная от Fx(x).
fx(x)dx = P(x < x £ x + dx) - элемент вероятности ( вероятность того, что случайная величина лежит в диапазоне между x и x + dx )
Свойства плотности вероятности :
1. f(x) ³ 0 - 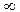 < x <
< x < 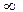
2. 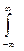 f(x)dx = 1
f(x)dx = 1
3. Fx(x) = 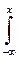 f(u)du
f(u)du
4. 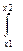 f(x)dx = P(x1 < x £ x2)
f(x)dx = P(x1 < x £ x2)
Средние значения и момент случайных величин
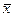 = E[x] = M[x] =
= E[x] = M[x] = 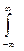 xf(x)dx -
xf(x)dx -
математическое ожидание величины x - центр тяжести стержня
1. Первый начальный момент ( начальный момент порядка n:
E[xn] = 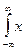 nf(x)dx )
nf(x)dx )
2. Второй начальный момент ( начальный момент второго порядка )
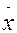 2 = E[x2] =
2 = E[x2] = 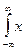 2f(x)dx
2f(x)dx
в технике - усредненный по времени квадрат случайного напряжения
или тока. Средняя мощность ( шума ).
3. Центральные моменты - моменты разности случайной величины Х и ее математического ожидания, то есть начальные моменты центрированной случайной величины. 

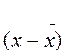 n
n  E[
E[ 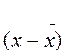 n] =
n] = 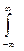
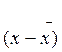 n f(x)dx
n f(x)dx
Центральные моменты характеризуют разброс случайной величины
относительно среднего ( математического ожидания ).
Первый центральный момент n=1 равен 0
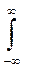
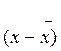 1 f(x)dx =
1 f(x)dx = 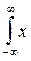 f(x)dx -
f(x)dx - 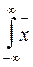 f(x)dx =
f(x)dx = 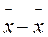
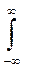 f(x)dx = 0
f(x)dx = 0
Второй центральный момент n=2 - дисперсия

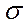 2x =
2x = 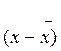 2 =
2 = 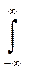
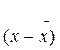 2 f(x)dx =
2 f(x)dx =  2 - (
2 - ( 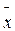 )2
)2
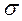 x - стандартное или среднеквадратичное отклонение
x - стандартное или среднеквадратичное отклонение
 Основные теоремы теории вероятности.
Основные теоремы теории вероятности.
Дата добавления: 2016-02-20; просмотров: 832;
