Основные задачи обработки измерений.

ОСНОВНЫЕ ЗАДАЧИ ОБРАБОТКИ ИЗМЕРЕНИЙ.

1. Основные задачи, решаемые в системах автоматизации (СА):

- регистрация данных и первичная обработка;

- прогнозирование процессов;

- многопараметрическое управлению.

2. Измерения:

2.1 погрешности (ошибки) измерений;

2.2 уравнения измерений.

3. Линеаризация задачи обработки данных.

4. Статистическая обработка измерений. Статистический и метрологический анализ.

5. Статистика и вероятность.

Измерения.

Наблюдения – регистрация различных фактов искусственного или естественного происхождения. Наблюдения подразделяются на качественные и количественные. Последние подразделяются на измерения и подсчёт.Измерения – средство регистрации физических величин и величин непрерывного типа. Обычно считают, что измерения в отличии от подсчёта состоит в сравнении измеряемой величины с эталоном. Измерения делятся на прямые и косвенные. При прямых измерениях непосредственно измеряется интересующая нас величина. При косвенных – измеряется некоторая функция интересующих величин:

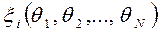
Прямое измерение – частный случай косвенного:

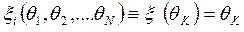
Современные измерительные приборы, как правило – многоступенчатые иерархические структуры:

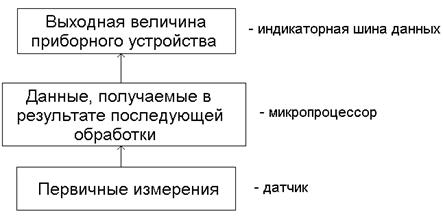
Пример: регистрация параметров механического процесса : - микропроцессор – первичная обработка на микро- (мили) – Э.В.М. – задача оценивания состояния.

Любому измерению обязательно присущи ошибки (погрешности).

Виды ошибок:

- личные;

- инструментальные;

- внешние;

- методические;

- ошибки модели;

- ошибки классификации.

Внешние ошибки – обусловлены влиянием на прибор внешней среды: толчки, вибрации и т.д.

Методические ошибки – ошибки метода: ошибки ................ , округлений, не учет различных факторов и т.д.

Ошибки модели: например, считаем, что движение равномерное, в то время как на самом деле оно равноускоренное и т.д.

Ошибки классификации: - при отношении измерений параметров постороннего объекта к изучаемому.

Все эти виды ошибок можно подразделить на систематические и случайные.

Грубой называется случайная ошибка, когда она превосходит паспортные характеристики прибора – «промах».

Характер образования суммарной ошибки измерения:

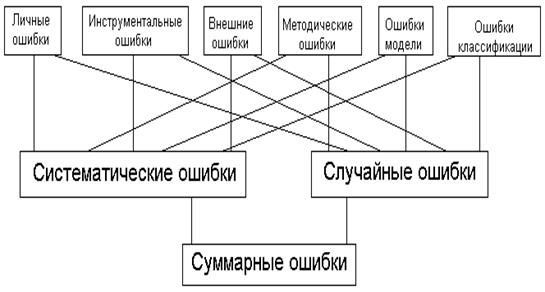
Провести точную грань между характером ошибок невозможно!

С учётом ошибок измерений связь между результатами измерений 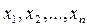и неизвестными параметрами 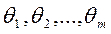описывается следующей системой уравнений: ,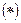

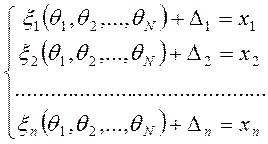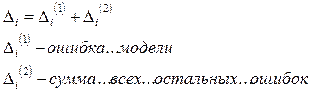
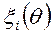- некоторые функции, чаще всего заранее заданные. Вид функции зависит от физики явления и от удобства её применения. Наиболее простые функции – линейные.

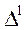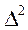Несовпадения истинных функций и принятых при обработке следует считать ошибками модели. Чаще всего предполагается, что известен вид функций распределения ошибок и . В противном случае определение вида функций распределения и их параметров входит в задачу обработки данных.

Основные задачи обработки измерений.

Чаще всего целью обработки является определение значений ряда параметров (физических), характеризующих с количественной стороны объект наблюдения. В отдельных случаях одновременно с этим ставится дополнительная задача определения параметров, характеризующих измерительную аппаратуру (точность измерений, наличие систематических ошибок и т.д.).

Основным объектом наибольшего исследования является система уравнений .

Обработка измерений ведётся в два этапа:

- определение неизвестных параметров по минимуму данных;

- обработка избыточных измерений.

1). по минимуму данных:

а). Суммарные ошибки полагают равными нулю;

б). Из фундаментальной системы отбирают N уравнений и решают их. (Если система линейная, решение ищется за один такт, если нелинейная – применяют итерационные методы).

Как только получено достаточно хорошее начальное приближение 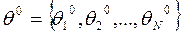, Сразу же появляется возможность упрощения системы уравнений . Обозначая 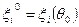, и полагая, что между малыми приращениями (вариациями) 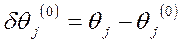определяемых параметров и 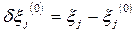измеряемой величины справедлива линейная зависимость 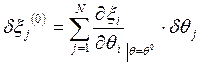(- все частичные производные вычислены в точке ),

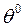Можно левые части уравнения 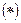заменить приближёнными соотношениями вида:

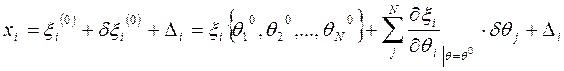
Вводя обозначения: 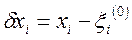, получаем

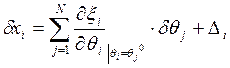
Обозначив 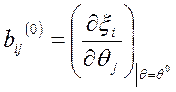, перепишем

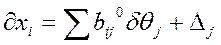
Теперь вместо непосредственного отыскания величин 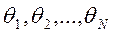целесообразно отыскивать поправки 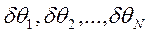к очередному приближению 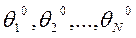, предполагая, что связь между измерениями 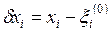и искомыми поправками 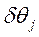, j=1,2,...,N – линейная - .

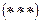Рассмотренная выше процедура - линеаризация задачи обработки данных. Поправки 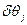обычно вычисляются при обработке данных избыточных измерений.

Если требуемая точность невелика, то можно ограничиться лишь получением начального приближения. Если решаемая задача – линейная, то можно сразу же приступить ко второму этапу, минуя первый.