Простейшие методы расчета нагрева я охлаждения электрических аппаратов и их частей 7 страница

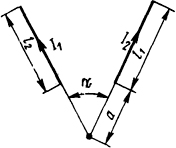
Рис. 2.5. Эскиз расположения проводников

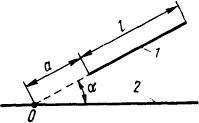
Рис. 2.6. Эскиз расположения проводников

2.1.18. Проводник 1 длиной l=2 м, по которому протекает ток i₁ = 10 кА, расположен под углом α=30° к проводнику 2, имеющему бесконечную длину, по которому протекает ток i₂=15 кΑ (рис. 2.6). Вычислить момент силы относительно точки О.и найти точку приложения равнодействующей, если а=0,5 м.

2.1.19. Определить усилие, действующее на нож рубильника (рис. 2.7), в момент, когда он размыкает цепь тока I = 500 А и между контактами горит дуга. Длина ножа рубильника t = 60 мм, угол между ножом и вертикалью α = 30°. Длины подводящих вертикальных шин принять бесконечными.

2.1.20. Определить усилие, с которым пластины ножа полюса разъединителя црижимаются к контактам во время протекания по ним тока к.з. I=50 кА, если полюс разъединителя состоит из двух параллельных пластин, расположенных на расстоянии а=20 мм друг от друга (рис. 2.8). Длина ножа разъединителя l=300 мм.

2.1.21. Определить усилие, которое во время к.з. стремится разомкнуть нож разъединителя, изображенного на рис. 2.9, ее; длина подводящих шин, расположенных горизонтально, бесконечна, а длина ножа разъединителя l = 350 мм. Ток к.з. I=35 кА

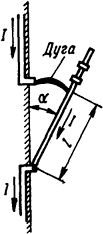
Рис. 2.7. Эскиз рубильника

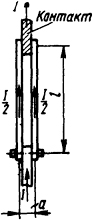
Рис. 2.8. Эскиз разъединителя

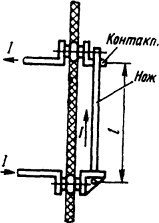
Рис. 2.9. Эскиз разъединителя

2.1.22. Определить электродинамическое усилие, действующее на 1 м круглого проводника диаметром d=20 мм. Провод ник расположен на расстоянии а/2=10 см вдоль ферромагнит ной стенки и по нему протекает ток I = 1000 А.

Решение. Так как диаметр проводника значительно меньше, чем рас стояние до ферромагнитной стенки, то к решению следует подходить, как и в случае бесконечно тонкого проводника. Методом зеркального изображени: найдем электродинамическое усилие, которое действует между данным про водником и его зеркальным изображением относительно поверхности ферро магнитной стенки с тем же током I.

Тогда F=μ₀I²l/(2πа)=4π10^-7·10⁶/(2π0,2)=1,0 Η, где μ₀=4π10^-7 Гн/м a=2·10·10^-2=0,2 м.

Ответ: F=1,0 H.

2.1.23. Определить усилие, с которым проводник, проложенный вдоль ферромагнитной стенки на расстоянии 20 см от нее притягивается к ней, если длина проводника l=0,5 м и по не му течет ток I=10 кА.

2.2. Расчет электродинамических усилий по энергетическим формулам

Приведенные в этом параграфе задачи дают возможность освоить метол расчета усилий по энергетическому принципу для наиболее часто встречающихся на практике случаев, т.е. для параллельных шин, полубесконечных петель, катушек, витков и других примеров, где индуктивность или взаимоиндуктивность контуров может быть выражена как функция координаты, в направлении которой вычисляется сила взаимодействия. При этом используются следующие расчетные формулы и соотношения.

Обобщенное усилие, действующее на проводник при i=const,

где W - электромагнитная энергия системы, Дж; g - обобщенная координата, м.

В линейных системах, поскольку

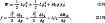
где L - индуктивность системы, Гн.

Электродинамическое усилие в проводниках при изменении поперечного сечения (усилие Двайта)

где D, d - соответственно диаметры большего и меньшего поперечного сечения, м; μ₀ - магнитная проницаемость вакуума, Гн/м.

2.2.1. Определить электродинамическое усилие, возникающее между двумя витками цилиндрического однослойного реактора, имеющего радиус R=1 м. Витки имеют шаг h=10 мм. По реактору протекает ток к.з. I=50 кА.

Решение. Для решения задачи воспользуемся формулой (2.8)

где W=I²M+W_соб - полная электромагнитная энергия системы; g - возможное перемещение в направлении действия усилия, т.е. dg=dh; W_соб - часть электромагнитной энергии, обусловленная собственной индуктивностью витков. При изменении координаты g остается неизменным W_соб, поэтому из формулы (2.1)

Если h=0,4R (это имеет место для условий задачи), взаимная индуктивность M=μ₀R[ln(8R/h)- 2] (см. табл. П.19). Тогда F_h=- I²μ₀R/h = - 50²·10·4π10^-7/(10·10^-9)= - 3140 Η.

Ответ: F=3140 H.

2.2.2. Определить усилия в условиях задачи 2.2.1, стремящиеся разорвать витки цилиндрического реактора, а также сжимающие проводники, изготовленные из круглого провода, радиус которого r =10 мм.

Решение. Полная электромагнитная энергия витков [1]

где взаимную индуктивность М определим как в задаче 2.2.1; L₁=L₂= L = μ₀R[ln(8R/r) - 7/4] - собственные индуктивности витков для r≪R; I₁ = I₂ = I (см. табл. П.19).

Доля энергии, приходящаяся на один виток, будет 0,5 W.

Из формулы (2.8) при g-R усилие, разрывающее виток,

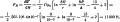
Эта сила равномерно распределена по дуге окружности витка. Сила же стремящаяся разорвать виток, F=F_R/(2π) = 1750 Η. Сила, сжимающая проводник в направлении его радиуса, определится из формулы (2.8) g=r;

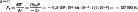
Эта сила равномерно распределена по всей поверхности витка.

Ответ: F= 1750 Η; F_r = 157000 Η.

2.2.3. Определить усилие, стремящееся разорвать круговой виток радиусом R=1 м, если по нему протекает ток I=40 кА

Диаметр поперечного сечения витка d=10 мм.

2.2.4. Определить усилие, действующее между двумя круговыми витка ми 1, 2 (рис. 2.10), если по виткам протекают токи i₁ = 10 кА, i₂=15 кА. Радиусы витков R₁ = 0,5 м, R₂=1 м диаметры проводников, из которы изготовлены витки, d₁=d₂ = 20 ММ. Расстояние между витками, находящимися в воздухе, h = 0,5 м. Вычислит усилия, разрывающие витки, и давления, сжимающие проводники, а также определить направления усилий.

Решение. Если h≈R, тο для двух витков взаимная индуктивность из табл. П. 19

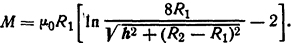
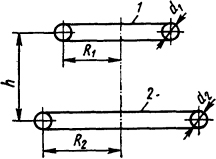
Рис. 2.10. Эскиз расположения витков

Тогда вертикальная составляющая усилия между битками в соответствии с (2.8)

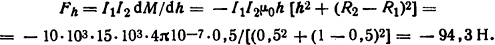
Знак минус свидетельствует о том, что с уменьшением расстояния взаимная индуктивность увеличивается.

Радиальные составляющие усилий

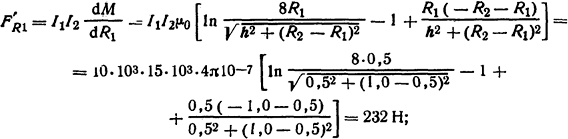
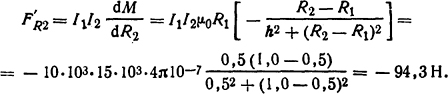
Знак минус свидетельствует о том, что данная сила сжимает виток 2.

Усилия, обусловленные собственными индуктивностями контуров, определим по формуле (2.10)

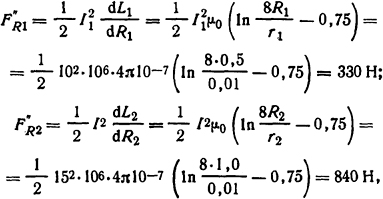
Тогда результирующие усилия, разрывающие витки, F_R1=F'_R1+F"_R1= 232+330=562 Η; F_R1= F'_R2+ F"_R2= -94,3+840=745,7 H. Эти усилия равномерно распределены по дугам окружностей соответствующих витков.

Усилия, стремящиеся разорвать витки,

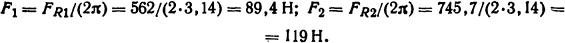
Для определения усилий, сжимающих витки, необходимо вычислить

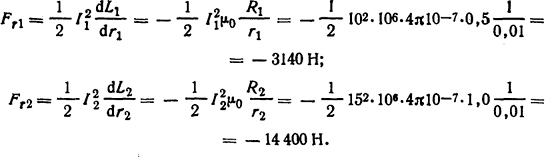
Эти усилия распределены равномерно по боковым поверхностям витков. Здесь знаки минус свидетельствуют о том, что происходит сжатие проводников. Следовательно, давления, действующие на боковые поверхности проводников,

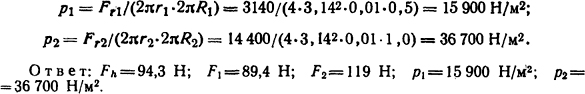
2.2.5. Вычислить электродинамическое усилие, с которым притягиваются друг к другу два круглых диаметром d = 5 мм

соседних витка цилиндрического реактора, имеющего средний радиус витков R = 0,5 м, если по реактору протекает ток I = 35 кА. Шаг витков реактора h=10 мм.

2.2.6. Определить усилия, разрывающие витки реактора, а также усилия, сжимающие проводники витков, для условий задачи 2.2.5 с той лишь разницей, что ток к.з. I=40 кА. Остальные данные без изменения. Вычислить также величины коэффициентов контуров электродинамических усилий в этих условиях.

2.2.7. Вычислить электродинамическое усилие, с которым взаимодействуют два круговых витка радиусом R = 0,8 м, лежащих в параллельных плоскостях на расстоянии 20 мм друг от друга и имеющих общую ось, если по одному из витков протекает ток I₁ = 10 кА, а по другому I₂=30 кА. Определить также величину коэффициента контура электродинамических усилий.

2.2.8. Для условий задачи 2.2.7 определить усилия, с которыми разрываются витки. Удовлетворяют ли они условиям прочности, если диаметры проводников d₁ = 10 мм и d₂ = 30 мм, а сами проводники изготовлены из меди, для которой допустимое напряжение на разрыв σ= 10⁴ Н/см². Вычислить также усилия, сжимающие проводники витков.

2.2.9. Определить усилие, действующее между двумя витками 1 и 2, радиусы которых R₁=0,25 м и R₂=0,4 м (см. рис. 2.10). Витки изготовлены из медных проводников круглого поперечного сечения диаметром d=10 мм и по ним протекают в одном направлении токи I1=I2=I=25 кА. Шаг витков h=0,25 м. Проверить, удовлетворяют ли условиям прочности поперечные сечения проводников; если не удовлетворяют, то подобрать ближайшие стандартные сечения, вычислить также давления, сжимающие проводники витков.

2.2.10. Для условий задачи 2.2.9 вычислить коэффициенты контуров электродинамических усилий между витками, разрывающих витки и сжимающих проводники витков.

2.2.11. Определить усилие, разрывающее виток прямоугольного сечения, размер которого a×b = 10×20 мм, средний радиус витка (R= 1,0 м. По витку протекает ток I=20 кА. Вычислить также давления, с которым сжимаются горизонтальные и вертикальные грани поперечного сечения.

Решение. Индуктивность витка радиуса R с прямоугольным поперечным сечением 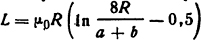(см. табл. П.19). Тогда усилие, разрывающее виток, определим из формулы (2.10) с учетом зависимостей задачи 2.2.1

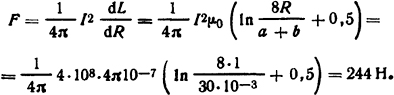
Давление, действующее на грани шириной а,

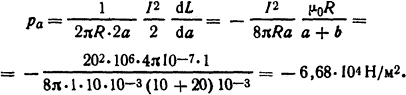
Давление, действующее на грань шириной b,

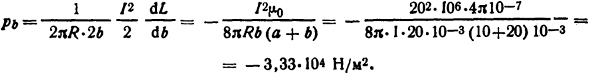
Ответ: F=244 Η; ρ_a = 6,68·10⁴ Н/м²; ρ_b = 3,33·10⁴ Н/м².

2.2.12. Определить усилие, действующее на виток в направлении изменения его радиуса, если по витку протекает ток I = 15 кА, виток имеет прямоугольное поперечное сечение с размерами a×b=5×10 мм, а его средний радиус R=0,5 м.

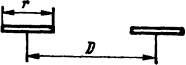
Рис. 2.11. Эскиз однослойной катушки индуктивности

2.2.13. Для условий задачи 2.2.12 вычислить давления, действующие на грани проводника, а также коэффициенты контуров электродинамических усилий, если поперечное сечение проводника выполнить квадратным с той же площадью.

2.2.14. Определить усилие, сжимающее витки однослойной катушки индуктивности, имеющей Ν=20 витков, размеры которой r=100 мм, D=500 мм (рис. 2.11), если по катушке протекает ток I=1,0 кА. Вычислить также усилие, стремящееся разорвать катушку.

Решение. Индуктивность однослойной катушки из табл. П. 19

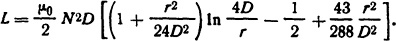
Тогда усилие, сжимающее витки катушки на основе формулы (2.10), равно

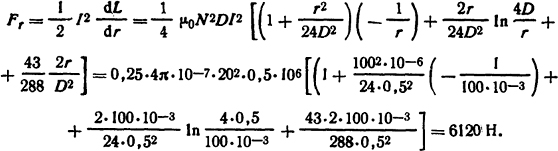
Это усилие равномерно распределено по дугам окружностей, ограничивающих витки катушки.

Усилие, разрывающее катушку, на основе формулы (2.10) равно

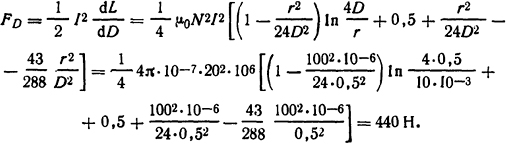
Это усилие распределено по окружности радиуса D/2.

Ответ: F=6120 Η; F_D=440 H.

2.2.15. Вычислить усилие, стремящееся сжать витки однослойной катушки индуктивности, имеющей 30 витков прямоугольного провода (см. рис. 2.11). По катушке протекает ток I=500 А, а ее размеры r=50 мм, D=300 мм.

2.2.16. Вычислить усилие, стремящееся разорвать однослойную катушку дискового реактора. Катушка состоит из 10 витков и по ней протекает ток I = 800 А, ее внутренний диаметр D_вн = 320 мм, наружный D_нар=480 мм. Определить также усилие, сжимающее витки катушки.

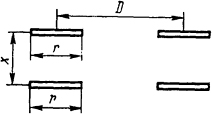
Рис. 2.12. Эскиз расположения плоских катушек

2.2.17. Определить усилие, с которым две одинаковые плоские катушки (рис. 2.12) притягиваются друг к другу, если по ним протекают токи I₁=I₂=I=100 A. Расстояние между катушками x =15 см, размеры катушек r = 10 см, D = 50 см, каждая катушка имеет по N = 20 витков провода.

Решение. Взаимная индуктивность двух плоских катушек из табл. П.19:

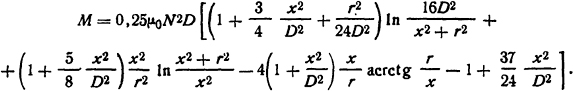
Тогда усилие, действующее между катушками, на основе формулы (2.10)

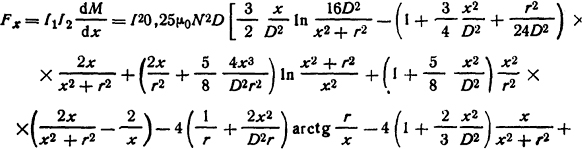
Ответ: F_x = 66,2 H.

2.2.18. Определить усилие, с которым отталкиваются Друг от друга два дисковых реактора, если по ним протекают токи I₁=80 кА, I₂=120 кА, расстояние между реакторами х=20 см (см. рис. 2.12), размеры реакторов одинаковы: r=15 см, D = 80 см. Реакторы выполнены из проводников прямоугольного поперечного сечения, имеют по 25 витков, высота поперечного сечения проводов намного меньше, чем расстояние между реакторами.

2.2.19. Для условий задачи 2.2.18 вычислить усилия, сжимающие проводники отдельных реакторов, и усилия, стремящиеся разорвать реакторы, а также определить коэффициенты контуров электродинамических усилий.

2.2.20. Определить усилие, с которым круглый проводник длиной l= 1 м и с током I = 1500 А притягивается к ферромагнитной стенке, если он находится от нее на удалении a=20 см. Ферромагнитная стенка имеет бесконечную магнитную проницаемость. Диаметр проводника 2r=10 мм. Вычислить также усилие, сжимающее проводник.

Решение. Если проводники расположены вдоль ферромагнитной стенки, то при расчете можно воспользоваться методом зеркальных отображений. Следовательно, индуктивность провода, расположенного вдоль ферромагнитной стенки на расстоянии а, равна индуктивности однофазной линии с проводами, расположенными на расстоянии b = 2а, т.е. для 1 м длины провода [10]

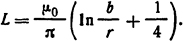
Тогда усилие, действующее на проводник, определится из формулы (2.10):

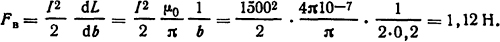
Усилие, сжимающее проводник,

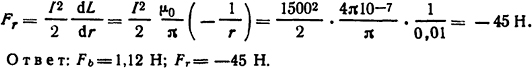
Ответ: F_b = 1,12 H; F_r= - 45 Η.

2.2.21. Определить значение электродинамического усилия, действующего на 1 м круглого проводника, расположенного вдоль ферромагнитной стенки на расстоянии 10 см от нее, если по проводнику протекает ток I=10 кА.

2.2.22. Вычислить усилие, действующее на проводник с током, находящийся в прямоугольном пазу ферромагнитной стенки, если по проводнику протекает ток I = 2,0 кА, магнитная проницаемость ферромагнитного материала μ = ∞, длина паза l = 100 мм, ширина δ = 10 мм.

2.2.23. Определить значение электродинамического усилия, которое возникает и стремится разомкнуть два круглых медных стержня диаметром d=10 мм. Торцы стержней обработаны под сферу радиуса r=40 мм, стержни стянуты силой F=98 H и по ним протекает ток короткого замыкания I=10 кА.

Решение. Так как здесь имеет место пластическая деформация (читатель это может проверить), то радиус площадки касания

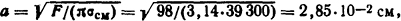
где σ_см=39300 Н/м² - напряжение смятия для меди (см. табл. П.16). По формуле Двайта (2.11) электродинамическое усилие

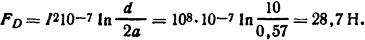
Ответ: F_D=28,7 Η.

2.2.24. Определить усилие, разрывающее проводник с током I=100 кА в месте, где проводник изменяет свое поперечное сечение от D=50 мм до d=20 мм.

Решение. Для нахождения усилия, разрывающего проводник, воспользуемся формулой Двайта (2.11)

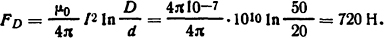
Ответ: F_D = 720 Η.

2.2.25. Электрический контакт образован путем сжатия двух круглых медных стержней силой F=400 H. Определить, с каким усилием эти стержни стремятся оттолкнуться друг от друга, если по ним протекает ток I=10 кА, диаметр стержней, изготовленных из твердой меди, d=20 мм, торцовые поверхности имеют радиус закругления r=10 мм.

2.2.26. Шина прямоугольного сечения 25×3 мм плавно переходит в шину размерами поперечного сечения 10×3 мм. Определить усилие, стремящееся разорвать шину, если по ней протекает ток I= 10,0 кА.

2.3. Расчет электродинамических усилий при переменном токе

В данном параграфе приведены задачи на расчет электродинамических усилий, когда по проводникам протекает переменный ток. Так как усилия, действующие на проводники при переменном токе, изменяются во времени,

то возникает необходимость в определении и правильном выборе собственной частоты колебаний элементов электрических аппаратов, подвергающихся воздействию этих усилий. Необходимо правильно рассчитать значения максимальных усилий, которые зависят от вида и места к.з. в системе. При этом используются следующие расчетные формулы и соотношения.

Электродинамическое усилие между двумя проводниками в однофазной системе

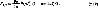
где μ₀=4π10^-7 Гн/м - магнитная проницаемость вакуума: I_m - максимальное значение тока при синусоидальном законе его изменения, Α; ω = 2πf - круговая частота тока c^-1; f - частота тока, Гц; k_1/2 - коэффициент контура электродинамических усилий.

Закон изменения тока при однофазном коротком замыкании

где а - постоянная затухания апериодической составляющей тока, с^-1.

Значение ударного тока короткого замыкания

где I - действующее значение установившегося тока короткого замыкания. Значение максимального отталкивающего усилия, действующего на крайние проводники в трехфазной системе при расположении проводников в одной плоскости на одинаковом расстоянии друг от друга,

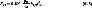
Значение максимального отталкивающего и притягивающего усилий, действующих на средний проводник в трехфазной системе при расположении проводников в одной плоскости на одинаковом расстоянии друг от друга

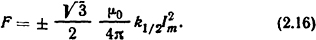
Значение максимального притягивающего усилия, действующего на крайние проводники в трехфазной системе при расположении проводников в одной плоскости на одинаковом расстоянии друг от друга,

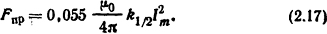
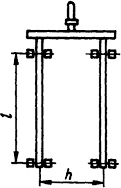
Рис. 2.13. Эскиз рубильника

2.3.1. Определить характер изменения во времени и значение электродинамического усилия, действующего на ножи рубильника (рис. 2.13), по которым протекает однофазный ток к.з. Установившееся значение тока I_уст = 800 А, частота f=50 Гц. Известно, что короткое замыкание произошло в удаленных от генератора точках сети. Размеры рубильника: l=80 мм, h = 70 мм.

Решение. Поскольку короткое замыкание произошло в удаленных от генератора точках сети, влиянием апериодической составляющей на электродинамическое усилие можно пренебречь [9], т.е. ток к.з. i = √2I_ycт sin ωt.

Тогда усилие взаимодействия между ножами рубильника в соответствии с формулой (2.7)

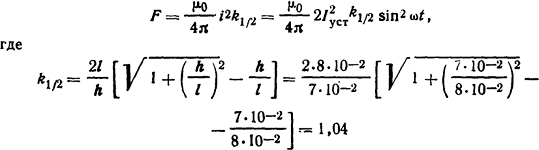
- коэффициент контура электродинамических усилий, определяемый по табл. П. 18; ω = 2π50=314 с^-1 - круговая частота тока. Тогда F = [4π10^-7/(4π)]2·800²·1,04 sin² ωt = 0,134 sin² ωt.

Разложив sin² ωt = (1 - cos²(ωt)/2, получаем F=0,067- 0,067 cos 628t. Очевидно, что максимальное значение усилия F_макс = 0,134 Н; среднее значение за период F_ср= 0,067 Н; минимальное F_мин = 0.

Ответ: F_макс=0,134 Н; F_ср= 0,067 Н; F_мин=0.

2.3.2. Для задачи 2.3.1 проверить, удовлетворяют ли условиям прочности и жесткости ножи рубильника, которые изготовлены из меди, поперечное сечение их имеет прямоугольную форму с размерами а×b = 3×15 мм. Ножи расположены широкими сторонами друг к другу.

Решение. Нож рубильника можно рассчитать как балку на двух опорах, т.е. σ_из=M/W_из≤σ_доп, где M=F_максl/8=0,134·80·10^-3/8=0,134·10^-2 Н·м - максимальное значение изгибающего момента; W_из=ba²/6=15·10^-3·3²·10^-6/6=22,5·10^-9 м³ - момент сопротивления; σ_доп=137·10⁶ Па - допустимое напряжение на изгиб для меди. Тогда

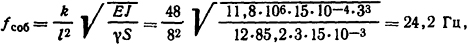
Следовательно, ножи рубильника удовлетворяют условиям прочности. Во избежание появления механического резонанса необходимо, чтобы частота собственных колебаний механической системы не была равна частоте возбуждающей силы, т.е. в нашем случае 100 Гц.

Для двух параллельных шин частота собственных колебаний

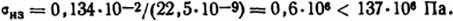
где k - коэффициент, учитывающий жесткости заделки ножа как балки на двух опорах. При жестко заделанном одном конце и свободном закреплении другого конца, это имеет место в случае рубильника, k=48 [1]; E=11,8×10⁶ Н/см² - модуль упругости материала (меди); γ=85,2 Н/см³ - удельный вес меди; S=3·15·10^-2 см² - площадь поперечного сечения; J = ba³/12 = 15·10^-4·3³/12 см⁴ - момент инерции поперечного сечения. Следовательно поскольку собственная частота меньше вынужденной, механический резонанс не будет иметь места.

Ответ: σ_из=0,6·10⁶ Па<σ_доп; f_coб=39,3 Гц<100 Гц.

2.3.3. Определить значения максимальных, средних и минимальных электродинамических усилий, действующих на ножи двухполюсного рубильника, изображенного на рис. 2.13. Через рубильник протекает однофазный ток к.з., значение которого в установившемся режиме к.з. I_уст=1000 А, а частота f = 50 Гц.

Длина ножей рубильника l=60 мм, расстояние между полюсами h = 55 мм. Влиянием апериодической составляющей тока к.з. пренебречь.

2.3.4. Написать зависимость усилия от времени электродинамического, возникающего между круглым проводником диаметром d=10 мм и ферромагнитной стенкой, вдоль которой проложен проводник с током, если по проводнику протекает ток к.з. I=1500 А частоты f = 50 Гц. Проводник находится на расстоянии h=20 см от стенки, магнитную проницаемость стенки принять равной μ=∞. Рассчитать усилие на длину проводника l=1 м.

2.3.5. Удовлетворяют ли условиям прочности и жесткости ножи рубильника, описанного в задаче 2.3.3, если поперечное сечение ножей является прямоугольным с размерами a×b = 3×20 мм. Ножи расположены широкими сторонами друг к другу и изготовлены из меди.

2.3.6. Определить значение максимального напряжения и частоту собственных колебаний отрезка проводника, имеющего длину 0,5 м и находящегося в прямоугольном пазу ферромагнитной стенки с бесконечной магнитной проницаемостью. По проводнику протекает переменный ток I=3 кА частоты f=50 Гц. Длина паза l=70 мм, ширина δ=20 мм, диаметр проводника d=10 мм. Проводник изготовлен из меди, на концах имеет жесткое закрепление.

2.3.7. Для условий задачи 2.3.4 сделать проверку проводника на прочность и жесткость, если известно, что проводник изготовлен из алюминия и через каждые 0,5 м имеет опорные изоляторы, в которых он закреплен.