Простейшие методы расчета нагрева я охлаждения электрических аппаратов и их частей 6 страница

Приведенные в этом параграфе задачи позволяют освоить тепловой рас чет электрических аппаратов и их частей с учетом совместного действия теплопроводности, конвекции и излучения, широко используя понятия теплового сопротивления и эквивалентных схем замещения.

В общем случае нагрева и охлаждения электрических аппаратов распространение теплоты происходит совместно тремя видами теплопередачи.

При расчетах в этом случае используются расчетные формулы и соотношения предыдущих параграфов данной главы.

1.6.1. Определить допустимый ток для алюминиевой круглой шины, изолированной слоем бумажной изоляции толщиной δ= 3 мм. Диаметр шины d=30 мм. Максимально допустимая температура наружной поверхности изоляции ϑ_нар = 50°С, шина расположена горизонтально в спокойном воздухе, температура которого ϑ₀ = 35°С.

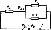
Рис. 1.22. Схема замещения изолированной шины

Решение. Составим эквивалентную схе му замещения для данного случая. В результате большой теплопроводности алюминия по сравнению с теплопроводностью бумажной изоляции тепловым сопротивлением шины пренебрегаем. Схема замещения изображена на рис. 1.22. Тепловые сопротивления на единицу длины шины определим из табл. П. 13:

где λ=0,14 Вт/(м·К) -теплопроводность бумаги (см. табл. П. 14); R=d/2+δ=15+3=18 мм; r=d/2=15 мм; k_т.к, k_т.и - соответственно коэффициет теплоотдачи конвекцией и излучением с поверхности бумажной изоляции к окружающей среде; R_т3=1/(k_т.и/F)=8,9/k_т.и.

Общее сопротивление тепловому потоку R_ΤΣ =0,207+8,9/(k_т.к+k_т.и). Тепловой поток на единице длины шины

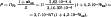
где ρ₀=2,62·10^-8 Ом·м (см. табл. П.7); ϑ_вн - температура внутренней поверхности изоляции; α=4,2·10^-3 К^-1 (см. табл. П.7).

Коэффициент теплоотдачи конвекцией определим по формуле (1.33)

Коэффициент теплоотдачи излучением определим как

где Nu_m = C[Gr Pr]_mⁿ определяем из формулы (1.38) при Pr_m = Pr_c, а р_и из формулы (1.52).

Тогда уравнениями для решения задачи будут PR_TΣ = ϑ_вн - ϑ₀, PR_т1 = ϑ_вн - ϑ_нар, т.е.

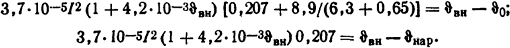
Решая эти уравнения совместно, получаем ϑ_вн = 55,6°С; I=350 А.

Ответ: ϑ_вн = 55,6°С; I=350 А.

1.6.2. Определить допустимую плотность тока для медной шины прямоугольного поперечного сечения с размерами 100×10 мм, которая изолирована слоем лакоткани толщиной δ = 2 мм. Допустимая температура наружной поверхности изоляции ϑ_доп=65°C, шина расположена в спокойном воздухе, температура которого ϑ₀=35°С.

1.6.3. Решить задачу 1.6.1 при условии, что задана допустимая температура внутренней поверхности изоляции ϑ_вн=80°С.

Решение. Исходными уравнениями для решения задачи будут

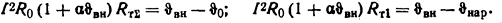
Подставляя числовые значения, получим следующую систему уравнений:

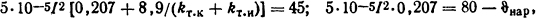
решая которую имеем

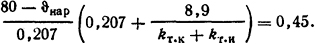
В последнем уравнении температура ϑ_нар входит в неявном виде в член (k_т.к+k_т.и), который зависит от температуры наружной поверхности. Построив зависимость у=f( ϑ_нар), решим это уравнение графически:

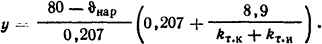
В точке, где график этой функции пересечет прямую у=45, получим искомое значение ϑ_нар=68,3°С (рис. 1.23).

Подставляя это значение в одно из уравнений системы, получаем I_доп = 1040 А.

Ответ: I_доп=1040 А.

1.6.4. Вычислить допустимую плотность постоянного тока медной шины прямоугольного поперечного сечения размером 100×10 мм, которая изолирована слоем лакоткани толщиной δ=4 мм. Шина расположена горизонтально в спокойном воздухе, температура которого ϑ₀=35°C Максимально допустимая температура поверхности изоляции ϑ_доп=80°С, степень черноты излучения для лакоткани ε=0,9 коэффициент теплопроводности λ = 0,16 Вт/(м·К).

1.6.5. Определить температуру поверхности стальной трубчатой шины, имеющей внутренний диаметр d_вн=2 дюйма, наружный ϑ_нар=60 мм, по которой протекает переменный ток I=225 А. Шина покрыта слоем бумажной изоляции толщиной δ = 5 мм. Определить также температуру наружной поверхности слоя изоляции, если шина расположена горизонтально в спокойном воздухе, температура которого ϑ₀=35°С.

1.6.6. Определить температуру наружной поверхности изоляции алюминиевой шины прямоугольного сечения размерами 80×10 мм, изолированной слоем стеклоткани толщиной δ = 3 мм. Шина расположена горизонтально и по ней протекает постоянный ток I=2800 А. Шина обдувается поперечным потоком воздуха, скорость которого w=1 м/с, а температура ϑ₀=25°C. Степень черноты излучения стеклоткани ε=0,85. При решении использовать критериальное уравнение для вынужденной конвекции при обтекании одиночного цилиндра [см. формулы (1.43) и (1.44)], в качестве определяющего размера взять d_э =4 S/П, S - площадь сечения; Π - периметр.

1.6.7. Определить допустимый ток для медной шины прямоугольного сечения, заключенной в прямоугольный короб, изготовленный из текстолита толщиной δ=4 мм. Шина расположена горизонтально в спокойном воздухе, температура которого ϑ₀ =35°С, ее поперечные размеры 50×6 мм. Зазор между коробом и шиной Δ=1 мм. Шина окислена, степень черноты излучения текстолита ε=0,8, а допустимая температура наружной поверхности текстолита ϑ_доп=80°С.

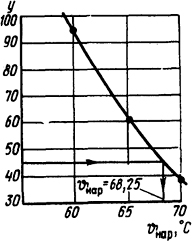
Рис. 1.23. График для определения температуры наружной поверхности шины

Решение. Эквивалентная схема замещения изображена на рис. 1.24, а.

Тепловые сопротивления на единицу длины шины определяем по формулам табл. П. 13, т.е.

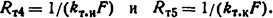
Общее сопротивление теплоотдачи с поверхности короба в окружающую среду

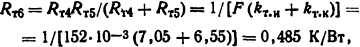
где k_т.к=7,05 Вт/(м²·К) определяем по критериальному уравнению (1.38); k_т.и=6,55 Вт/(м²·К) - из уравнения для теплоотдачи излучением [см. формулу (1.52)], F=2(50+2+8+6+2+8) = 152·10^-3 м² -площадь охлаждающей поверхности наружной части короба длиной 1 м.

Тогда тепловой поток через сопротивление R_т6

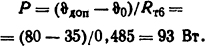
Тепловое сопротивление стенки короба толщиной δ = 4 мм

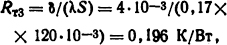
где λ=0,17 Вт/(м·К) (см. табл. П.14), S = 2(50+2+6+2) = 120·10^-3 м².

Температура внутренней стенки короба

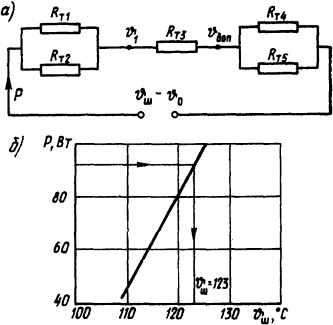
Рис. 1.24. Схема замещения (а) и зависимость мощности источников теплоты от максимальной температуры (б)

В воздушном зазоре Δ=1 мм имеет место теплопередача стесненной конвекцией и излучением. Так как расчет стесненной конвекции в конечном итоге сводится к расчету распространения теплоты теплопроводностью, то вычисления тепловых сопротивлений R_т1 = Δ/(λ_1эF₁) и R_т2 = Δ/(λ_2эF₁) производим как расчет тепловых сопротивлений плоской стенки без внутренних источников теплоты. Здесь λ_1э определим из формулы (1.40) для стесненной конвекции, а λ_2э - из приведенных ниже соображений. Если ϑ_ш - температура поверхности шины, то количество теплоты, передаваемое от шины к коробу путем излучения с поверхности шины, определится из формулы (1.51)

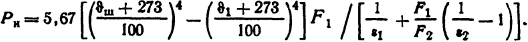
Если предполагать, что теплопередача идет теплопроводностью, то Р_и=λ_2э( ϑ_ш- ϑ₁)F₁/Δ, откуда λ_2э=P_иΔ/( ϑ_ш- ϑ₁). Так как R_т1 и R_т2 - параллельно включенные сопротивления, то R_т7=R_т1R_т2/(R_т1+R_т2)=Δ/[(λ_1э+λ_2э)]. Примем F₁=F₂, тогда ( ϑ_ш- ϑ₁)/R_т7=Р.

Поскольку ϑ_ш входит неявно в λ_1э, а следовательно, и в R_т7, задачу следует решать подбором. Задаваясь произвольными значениями ϑ_ш, построим график функций Р=Р( ϑ_ш) (рис. 1.24, б). В точке пересечения кривой с прямой Р=93 Вт определим искомое значение ϑ_ш=123°С.

Из выражения I²ρ₀(1+α ϑ_ш)/S = Ρ допустимый ток

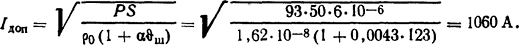
Значения ρ₀ и α приведены в табл. П.7; S=50·6·10^-6 м² - площадь поперечного сечения шины.

Ответ: I_доп=1060 А.

1.6.8. Решить задачу 1.6.7 при условии, что зазор между шиной и коробом δ=2 мм. Остальные данные остались без изменения.

1.6.9. Определить температуру наружной поверхности короба, в который заключена алюминиевая шина с размерами поперечного сечения 60×6 мм. Короб изготовлен из гетинакса толщиной δ=3 мм. По шине протекает переменный ток I=880 А частоты f=50 Гц. Шина расположена горизонтально в спокойном воздухе, температура которого ϑ₀=35°С. Степень черноты излучения с поверхности гетинакса ε =0,7, поверхность шины покрыта масляной краской, зазор между шиной и коробом Δ = 3 мм.

1.6.10. Найти температуру круглой медной шины диаметром d = 38 мм, которая проходит через достаточно длинную медную трубу, внутренний диаметр которой d_вн=40 мм, наружный d_нар=45 мм. По шине протекает постоянный ток I=1500 А. Шина расположена горизонтально и концентрично с трубой в спокойном воздухе, температура которого ϑ₀=35°С. Коэффициент теплоотдачи с наружной поверхности трубы в окружающий воздух k_т = 5,2 Вт/(м²·К).

1.6.11. Определить допустимую плотность тока в круглой медной шине диаметром d = 38 мм, расположенной горизонтально и концентрично в достаточно длинной медной трубе с внутренним диаметром d_вн=40 мм, наружным d_нар=45 мм. Труба имеет слой изоляции толщиной δ=20 мм из бакелизированной бумаги и находится в спокойном воздухе, температура которого ϑ₀ = 35°С. Допустимая температура для данной шины ϑ_доп= 115°С, степень черноты излучения для бакелита ε₁ = 0,9, для окисленной меди ε₂ = 0,6. Эквивалентная схема замещения такая же, как и в задаче 1.6.7 (если пренебречь тепловым сопротивлением медной трубы). Решение задачи отличается тем, что необходимо вести двойное графическое построение. Вначале строим график функции Р = Р( ϑ_ш), предварительно задавшись произвольным значением температуры наружной поверхности изоляции. После определения ϑ_ш для заданного значения ϑ_нар строим график ϑ_ш = f( ϑ_нар) и для заданного значения ϑ_доп определяем ϑ_нар и, следовательно, возможную отводимую мощность с поверхности изоляции. Зная мощность и температуру шины, определяем значение допустимой плотности тока.

1.6.12. Определить допустимый ток для медной трубы с размерами d_вн=12 мм, d_нар=15 мм, по которой протекает вода со

скоростью w=0,5 м/с. Температура воды на входе в трубу ϑ_вх= 20°С, на выходе ϑ_вых = 30°С. Труба расположена горизонтально в спокойном воздухе, ее поверхность окрашена масляной краской. В результате длительной эксплуатации внутренняя поверхность трубы покрылась слоем накипи, толщина которого δ = 1 мм, а теплопроводность λ=0,8 Вт/(м"К). Допустимая температура наружной поверхности трубы ϑ_доп=50°С, температура окружающего воздуха ϑ₀ = 35°С.

Решение. Схема замещения показана на рис. 1.25, где R_т1=δ/(λS) = 1·10^-3/(0,8·3,14·10·10^-3) = 0,04 К/Вт- тепловое сопротивление слоя накипи; R_т2=1/(k_т.внF_вн) = 1/2800·3,14·10·10^-3 = 0,0113 К/Вт - тепловое сопротивление теплоотдачи в воду; k_т.вн = 2800 Вт/(м²·К) определяем из критериальных уравнений (1.47) и (1.49) при протекании жидкости в гладких трубах. R_т3=1(k_т.нарF_нар) = 1/(10,6·3,14·15·10^-3)=2 К/Вт - тепловое сопротивление теплоотдачи с наружной поверхности воздуху; k_т.нар = 10,6 Вт/(м²·К), определяем из условия теплоотдачи конвекцией и излучением [1];

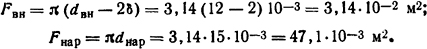
Количество теплоты, отдаваемое в воздух,

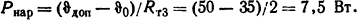
Количество теплоты, отдаваемое в воду,

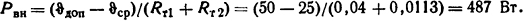
где ϑ_ср = 0,5( ϑ_вх+ ϑ_вых) =0,5(20+30) =25°С.

Суммарное количество теплоты, отведенное от трубы, Р=Р_вн+P_нар = 487+7,5=494,5 Вт. Теплоту, выделенную в трубе, определим по формуле Р=I²ρ₀(1-α ϑ_доп)/S, откуда допустимый ток

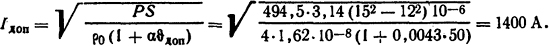
Ответ: I_доп=1400 А.

1.6.13. Решить задачу 1.6.12 при условии, что слой накипи удален полностью. Остальные данные оставить без изменений.

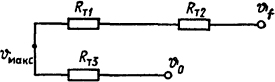
Рис. 1.25. Схема замещения

ГЛАВА 2. ЭЛЕКТРОДИНАМИЧЕСКИЕ ДЕЙСТВИЯ ТОКОВ

2.1. Расчет электродинамических усилий с использованием закона Био - Савара - Лапласа

В этом параграфе приведены задачи на вычисление электродинамических усилий на прямолинейные участки проводников как с учетом влияния размеров поперечного сечения, так, и без него.

В ряде случаев электродинамические усилия довольно легко можно вычислить, используя закон Био - Савара - Лапласа для определения значений:

и направления магнитной индукции. При этом используются следующие рас четные формулы и соотношения.

Формула Ампера для определения электродинамических усилий (э.д.у.) действующих на линейный проводник с током, находящийся в однородном магнитном поле,

где i - значение тока, А; l - длина проводника, м; В - магнитная индукция, Тл; γ - угол между направлением тока и вектором индукции.

Формула Ампера в векторном виде

Формула Ампера в дифференциальной форме в векторном виде

Закон Био - Савара - Лапласа

где i - ток в проводнике, A; dl - элементарный участок проводника, м; α - угол между направлением тока и направлением радиуса-вектора r от середины участка dl до точки пространства, в которой определяется напряженность магнитного поля dH; r - длина вектора r, м.

Закон Био - Савара - Лапласа в векторной форме

Элементарное электродинамическое усилие, действующее со стороны элементарного проводника длиной dl₂ (м), с током i₂ (А), на элементарный проводник длиной dl₁ (м) с током i₁ (А), находящегося на расстоянии r (м) от проводника dl₂,

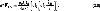
где μ₀ - магнитная проницаемость воздуха, μ₀ = 4π·10^-7 Гн/м.

Электродинамическое усилие, Н, между двумя проводниками с токами i₁ и i₂, А:

где k_1/2 - коэффициент контура электродинамических усилий (см. табл. П. 18).

2.1.1. Определить электродинамическое усилие, действующее на 10 м прямолинейного бесконечно тонкого уединенного проводника с током к.з. I=50 кА. Проводник находится в поле земли и расположен под углом γ =30° к плоскости магнитного меридиана. Горизонтальная составляющая напряженности магнитного поля Η =12,7 А/м, а угол наклонения β = 72°.

Решение. Действующее на проводник усилие определим из закона Ампера [см. формулу (2.1)].

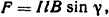
где Β = μ₀Η, μ₀=4π10^-7 Гн/м.

Тогда горизонтальная составляющая индукции земного поля B_г=4π·10^-7·12,7 = 0,16·10^-4 Тл; вертикальная составляющая B_в=B_г tg β = 0,16×

×10^-4tg 72° = 0,49·10^-4 Тл. Определим две составляющие силы, действующие на проводник:

от горизонтальной составляющей вектора индукции

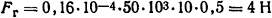
и от вертикальной

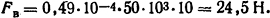
Суммарное усилие, действующее на проводник,

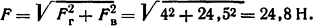
Ответ: F=24,8 H.

2.1.2. Определить усилие, действующее на 1 м длины прямолинейного проводника, по которому протекает постоянный ток I=10 кА, если проводник находится в однородном постоянном магнитном поле, магнитная индукция в каждой точке проводника B = 0,1 Тл, а угол между вектором индукции и направлением тока γ =30°.

2.1.3. Определить значение электродинамического усилия, с которым притягиваются друг к другу два параллельных круглых, бесконечно длинных проводника, находящиеся друг от друга на расстоянии а=1 м, когда по ним кратковременно протекают токи i₁ = 10 кА, i₂ = 20 кА. Диаметры проводников соответственно равны d₁=10 мм и d₂=20 мм. Расчет усилия провести на длине l=1 м.

Решение. Определим усилие, действующее на 1 м проводника. Поскольку проводники бесконечно длинные, напряженность магнитного поля на оси второго проводника от тока в первом

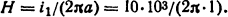
Так как диаметры проводников намного меньше, чем расстояния между ними, то расчет можно вести как для бесконечно тонких проводников. Тогда усилие между проводниками в соответствии с формулой (2.1)

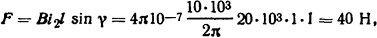
где sinγ=1, так как проводники лежат в одной плоскости; B = μ₀H; μ₀ = 4π·10^-7 Гн/м.

Ответ: F=40 H.

2.1.4. Определить величину и направление усилия, действующего между двумя параллельными проводниками длиной l = 4 м, по проводникам, находящимся в воздухе на расстоянии а=3 м друг от друга, протекают постоянные токи i₁ = 10 кА, i₂=15 кА.

2.1.5. Определить величину коэффициента контура электродинамических усилий для условий задачи 2.1.4.

2.1.6. Определить величину коэффициента контура электродинамических усилий для системы двух параллельных проводников длиной l=10 м, находящихся друг от друга на расстоянии а = 2 м.

2.1.7. Определить усилие, которое действует на проводник 3 со стороны проводников ₁ и 2 (рис. 2.1), если по проводникам протекает ток i=100 кА, проводник имеет бесконечную длину, а провод ники 2 и 3 - соответственно l₂= 1 м l₃=2 м. Проводники круглые диаметром d=40 мм. Вычислить также момент усилия относительно точки В и определить точку приложения равно действующей усилия на проводник 3.

Решение. Напряженность поля в точке x проводника 3 от тока, протекающего π проводнику 1, определим на основании закон Био - Савара - Лапласа, причем, поскольк диаметры проводников значительно меньше расстояний между ними, расчет будем производить как для бесконечно тонкопроводников.

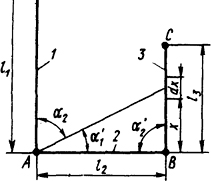
Рис. 2.1. Эскиз расположения проводников

Тогда расстояние от точки приложения равнодействующего усилия F будет равно L = M_B/F= 4960/7360 =0,674 м.

Ответ: F=7360 Η; М_B = 4960 Н·м; L = 0,674 м.

2.1.8. Определить величину электродинамического усилия, возникающего между двумя расположенными параллельно друг другу шинами прямоугольного сечения h×b = 100×10 мм на длине l = 2 м. Расстояние между осями шин α =20 мм, по ним протекает ток к.з. I=54 кА. Шины находятся в воздухе вдали от ферромагнитных частей, и ток по их сечению распределен равномерно. При решении задач учесть влияние поперечных размеров на величину электродинамического усилия. Шины расположены широкими сторонами друг к другу.

Решение. Величина электродинамического усилия [1] F=2·10^-7 Для данного случая расположения проводников величина (а-b)/(b+h) = (20-10)/(10+100) = 0,091; b/h=10/100=0,1. Тогда из рис. П.12 коэффициент формы k_ф=0,44. Следовательно,

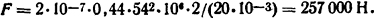
Ответ: F=257000 H.

2.1.9. Определить электродинамическое усилие, возникающее между двумя шинами, расположенными параллельно друг другу узкими сторонами, если по ним протекает ток к.з. I=60 кА, расстояние между осями шин а=110 мм, размеры поперечного сечения шин 100×10 мм. Шины находятся в воздухе вдали от ферромагнитных частей, и ток по их сечению распределен равномерно. Расчет усилия произвести для длины участка шин l=3 м, при этом учесть влияние поперечных размеров.

2.1.10. Определить электродинамическое усилие, действующее на проводник 1, со стороны проводника 2 (рис. 2.2), если по проводникам протекает постоянный ток I=12 кА, а длины участков соответственно l₁ = 1 м, l₂ = 2 м. Проводники круглые диаметром d=10 мм и находятся в воздухе на достаточном удалении от ферромагнитных частей.

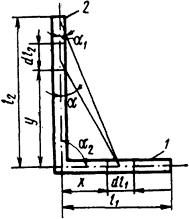
Рис. 2.2. Эскиз расположения проводников

Решение. Выделим элементы проводников dl₁ и dl₂ и определим элементарную силу, действующую со стороны элемента dl₂ на элемент dl₁. Так как проводники находятся в одной плоскости, то со стороны проводника 2 на проводник 1 действует элементарная сила

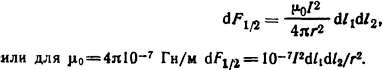
Суммарная сила, действующая на проводник 1,

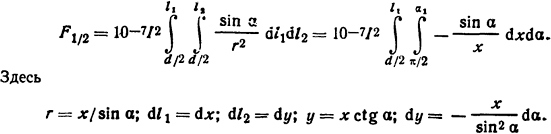
После интегрирования и учитывая, что cos α₁ = 1₂/√l₂² + х², получаем

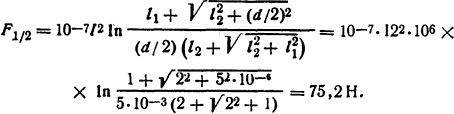
Ответ: F_1/2=75,2 H.

2.1.11. Определить электродинамическое усилие, действующее на проводник 1 для условий задачи 2.1.10 (см. рис. 2.2) той лишь разницей, что проводник 2 имеет бесконечную длин. Остальные данные без изменения.

2.1.12. Определить электродинамическое усилие, действующее на перемычку, соединяющую две параллельные шины круглого сечения (рис. 2.3), если по шинам и перемычке протекает

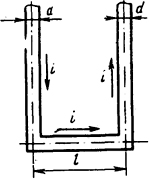
Рис. 2.3. Эскиз расположения шин

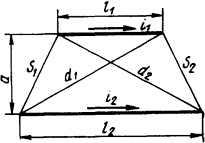
Рис. 2.4. Эскиз расположения шин

постоянный ток I=15 кА, диаметр шин и перемычки d=20 мм расстояние между шинами а=0,5 м, шины имеют бесконечную длину.

2.1.13. Определить электродинамическое усилие для условий задачи 2.1.10, действующее на проводник 2 со стороны проводника 1.

2.1.14. Определить значения коэффициентов контура электродинамических усилий для условий задач 2.1.10 и 2.1.13.

2.1.15. Определить электродинамическое усилие, действующее между параллельно расположенными шинами (рис. 2.4), если I₁ = 10 кА, I₂=15 кА, l₁ = l м, l₂=1,5 м, а = 0,5 м.

Решение. Электродинамическое усилие определим по формуле (2.7) F_1/2=μ₀I₁I₂k_1/2/4π. Из табл. П.18 коэффициент контура электродинамических усилий

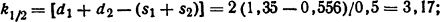
для воздуха μ₀=4π10^-7 Гн/м.

Тогда F_1/2= 10^-7·10·10³·15·10³·3,17 = 47,6 Η.

Ответ: F_1/2=47,6 H.

2.1.16. Решить задачу 2.1.15 при условии, что проводник 2 имеет бесконечную длину. Остальные данные без изменения.

2.1.17. На рис. 2.5 изображены два отрезка проводников с токами. Определить электродинамическое усилие между этими проводниками, если по ним протекают токи i₁ = 20 кА, i₂=30 кА, угол α = 30°, длина проводников l₁ = l₂=1,5 м, a =0,5 м.