Простейшие методы расчета нагрева я охлаждения электрических аппаратов и их частей 3 страница

1.3.11. Решить задачу 1.3.10 при условии, что нагреватель обдувается воздухом, температура которого ϑ₀=10°C, скорость потока w = 1 м/с.

1.3.12. Определить температуру поверхности и значение коэффициента теплоотдачи круглой медной шины диаметром d=25 мм, если по ней пропускается постоянный ток I=2900 А. Шина охлаждается поперечным потоком трансформаторного масла, скорость которого w=1 м/с, температура ϑ_ж=20°С.

Решение. Для данной задачи из формулы (1.36)

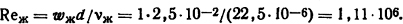
Так как 10³≤Rе_ж<2·10⁵, то для нахождения коэффициента теплоотдачи воспользуемся формулой (1.44)

Так как Рr_с и потери в шинопроводе зависят от его температуры, то задачу решают подбором. Из равенства

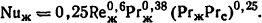
Задаваясь различными температурами ϑ_с, определим коэффициенты теплоотдачи из формул (1.33) и (1.44) и токи для этих температур:

По этим данным строим график (рис. 1.5) и для I=2900 А находим температуру ϑ_c=68,5°С; k_т=925 Вт/(м²·К).

Ответ: ϑ_c = 68,5°С; k_т=925 Вт/(м²·К).

1.3.13. Определить температуру поверхности и значение коэффициента теплоотдачи для условий задачи 1.3.12, если по шине пропускается ток (переменный) I=5 кА частоты f=50 Гц и шина охлаждается потоком воды.

1.3.14. Определить коэффициент теплоотдачи и тепловой поток с внутренней поверхности трубы из нержавеющей стали, по которой протекает постоянный ток, в результате чего температура внутренней поверхности ϑ=75°С. Внутри трубы протекает вода со скоростью w = 0,1 м/с, внутренний диаметр трубы d_вн=7,6 мм, длина трубы l=1 м, а температура воды на входе ϑ_вх= 20°, на выходе ϑ_вых=65°С.

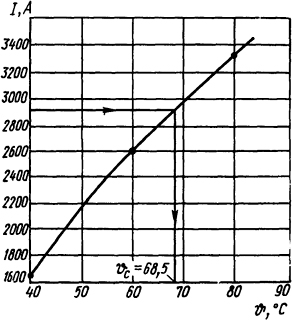
Рис. 1.5. Построение графика к задаче 1.3.13 и определение температуры поверхности шин

Решение. Воспользуемся критериальными уравнениями для вынужденной конвекции при протекании жидкостей в трубах. При этом необходимо выяснить характер течения, для чего следует вычислить критерий Рейнольдса

При определяющей температуре ϑ_ж=( ϑ_вх+ ϑ_вых)/2=42,5°С определим значения физических параметров воды:

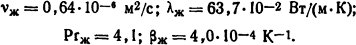
Кроме того, Рr_с = 2,39 при ϑ_c = 75°С. Тогда в соответствии с формулой (1.36)

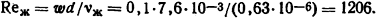
Так как Re_ж =1206<2200, то движение воды в трубе будет ламинарным, поэтому следует воспользоваться формулой (1.47)

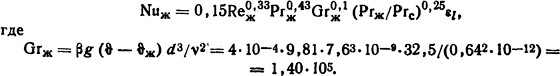
Так как l/d=1000/7,6 > 50, то из табл. 1.4 ε_l=1. Подставляя числовые значения, вычисляем

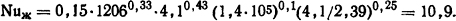
Тогда коэффициент теплоотдачи из формулы (1.33)

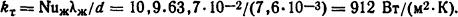
Тепловой поток с внутренней поверхности трубы в соответствии с формулой (1.12)

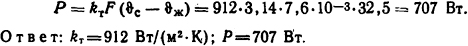
1.3.15. Определить коэффициент теплоотдачи с горизонтальной крышки масляного бака, обдуваемой потоком воздуха со скоростью w=2 м/с. Продольный размер крышки a=1,0 м, поперечный b=0,5 м, температура поверхности ϑ_с = 50°С, температура набегающего потока воздуха ϑ₀=20°C.

1.3.16. Определить длительно допустимый переменный ток для условий задачи 1.3.14. При ϑ=75°С удельное сопротивление нержавеющей стали ρ=0,85·10^-6 Ом·м, а наружный диаметр трубы d_нар=8 мм.

1.3.17. Определить температуру внутренней поверхности трубы из нержавеющей стали, которая включена в электрическую цепь переменного тока. Длина трубы l=2600 мм, наружный диаметр d_нар=12,4 мм, внутренний d_вн=12,0 мм. По трубе протекает вода со скоростью w=1 м/с и пропускается ток I=260 А, а температура воды на входе и выходе соответственно равна 20 и 60°С. Удельное сопротивление нержавеющей стали принять не зависящим от температуры ρ=0,85·10^-6 Ом·м.

Решение. Задачу будем решать подбором, поскольку в критериальное уравнение входит величина Рr_с, а значение Прандтля зависит от температуры (см. табл. П. 10).

Для ϑ_ж=( ϑ_вх+ ϑ_вых)/2=(20+60)/2=40°С критерий Рейнольдса в соответствии с формулой (1.36) Re_ж=_wd/ν_ж=1·12·10^-3/(0,659·10^-6) = 18200. Так как Rе_ж=18200>10000, то движение жидкости в трубе будет турбулентным и для решения задачи можно воспользоваться критериальным уравнением из формулы (1.49)

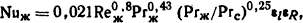
где в соответствии с табл. 1.5 и формулой (1.50) ε_l=1 и ε_R = 1.

Подставив известные величины в написанное уравнение и произведя возможные сокращения, получим Nu_ж=143/Рr_с^0,25. Коэффициент теплоотдач определим по формуле (1.33) k_т = Nu_жλ_ж/d, где λ_ж= 63,5·10^-2 Вт/(м·К).

Из формулы I²ρ₀l/S=k^тF( ϑ₀- ϑ_ж) определим перепад температур:

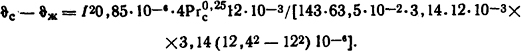
После возможных сокращений получаем функциональную связь между ( ϑ_с- ϑ_ж), I и Рr_с, т.е.

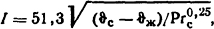
представленную ниже:

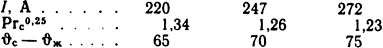
По этим данным строим график I=φ( ϑ_с) (рис. 1.6) и по заданному значению тока I=260 А определяем температуру внутренней стенки трубы ϑ_с = 72,5°С.

Ответ: ϑ_c = 72,5°С.

1.3.18. Вычислить допустимый ток катушки индуктивности, выполненной из медной трубы, намотанной на цилиндрическую оправку радиуса R = 120 мм. Труба имеет внутренний диаметр d=12 мм, толщину стенки δ=2 мм и по ней с целью охлаждения пропускают воду со скоростью w=1 м/с. Температуры воды на входе ϑ_вх = 25°С, на выходе ϑ_вых = 55°С. Катушка имеет четыре витка. Температура внутренней поверхности трубы не должна превышать ϑ_доп = 65°С. Определить также количество теплоты, отводимое водой от катушки.

1.3.19. Определить требуемую скорость воды и температуру внутренней стенки медной трубы, длина которой l=1 м, внутренний диаметр d_вн = 20 мм, наружный d_нар = 30 мм. По трубе протекает ток I=15000 А.

Температура воды водопроводной сети ϑ_вх=25°С, а допустимая температура воды на выходе из трубы ϑ_вых = 45°С.

Решение. Средняя температура воды в трубе в соответствии с (1.48)

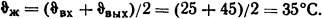
Если средняя температура внутренней стенки трубы будет выше средней температуры жидкости, то только в этом случае будет иметь место теплоотдача от стенки трубы к воде. Зададимся средней температурой стенки трубы ϑ_c = 50°C. Тогда мощность, выделяемая в трубе при протекании по ней тока,

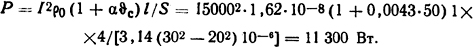
Зная температуру воды на входе в трубу и выходе из нее, определим необходимую скорость движения воды, исходя из условия, что мощность, выделяемая в трубе, должна восприниматься и уноситься водой. Мощность, уносимая водой,

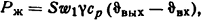
где S - площадь поперечного сечения трубы; w₁ - скорость воды; γ = 993 кг/м³ - плотность воды; с_р = 4174 Дж/(кг·К)-удельная теплоемкость воды при ϑ_ж и постоянном давлении р. Тогда 11300=3,14·20²·10^-6w₁·993·4174(45-25)/4, откуда w₁= 0,436 м/с.

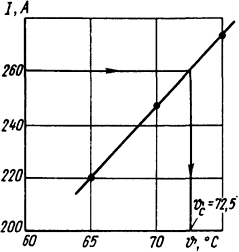
Рис. 1.6. Построение графика к задаче 1.3.17 и определение температуры поверхности трубы

Для воды при ϑ_ж=35°С из формулы (1.36)

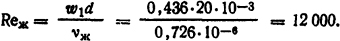
В соответствии с (1.49) критериальное уравнение будет иметь вид

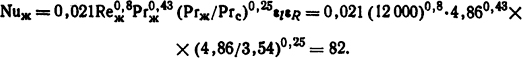
Здесь ε_l=1, ε_R = 1.

Коэффициент теплоотдачи определим по формуле (1.33) [см. табл. 1.5 и формулу (1.50)]

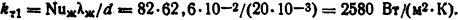
Из формулы (1.12) P₁=k_т1F( ϑ_c1 - ϑ_ж), температура поверхности трубы

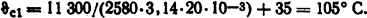
Первоначально заданная температура стенки была 50°С. Поскольку получилось большое расхождение, проведем второе приближение. Зададимся ϑ_с2=(50+105)/2≈80°С, тогда Р₂=12500 Вт; w₂=0,485 м/с; k_т2=3150 Вт/(м²·К); ϑ_c2=98°C.

Третье приближение ϑ_с3=(80+98)/2≈90°С дает P₃=12 900 Вт; w₃=0,5 м/с; k_т3=3360 Βт/(м²·Κ); ϑ_с3=94°С. Эту точность можно считать удовлетворительной.

Ответ: w=0,5 м/с; ϑ_c=94°С.

1.3.20. Решить задачу 1.3.19 при условии, что по трубе протекает ток I=10000 А; все остальные данные без изменения.

1.3.21. Определить необходимый расход воды и температуру внутренней поверхности стальной трубчатой шины, по которой протекает переменный ток I=6000 А частоты f=50 Гц. Шина охлаждается проточной водой, имеет длину /= 1 м, внутренний диаметр d_вн=2 дюйма, наружный d_нар=60 мм. Температура воды на входе в трубу ϑ_вх=20°С, на выходе из нее ϑ_вых=25°С.

1.3.22. Вычислить расход воды и значение тока, который можно пропустить через отрезок алюминиевой круглой шины длиной 1 м. Температура воды на входе шины ϑ_вх=25°С, а на выходе - ϑ_вых=55°С. Допустимая температура внутренней поверхности Шины ϑ_c = 95°С, внутренний диаметр шины d_вн=45мм, наружный d_нар=50 мм.

Решение. Скорость охлаждающей воды определим из уравнения

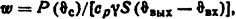
Тогда критерий Рейнольдса из уравнения (1.36)

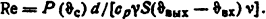
Для ламинарного режима движения жидкости из формулы (1.47)

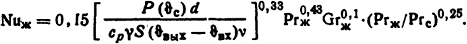
Так как из формулы (1.33) коэффициент теплоотдачи k_т=Nu_жλ_ж/d, а ϑ_c - ϑ_ж=Р( ϑ_с)/(k_тF), то, подставляя в последнее равенство все необходимые

значения и произведя вычисления, получим P( ϑ_с)=485 Вт. В данном случае Rе_ж=188<2200, следовательно, движение будет ламинарным и, следовательно, примененная формула справедлива. Допустимый ток

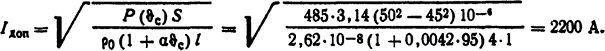
При этом необходимый расход воды

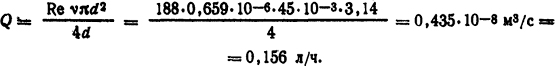
Такой расход воды можно обеспечить за счет автономной водовоздушной системы [3].

Ответ: I=2200 A; Q = 0,156 л/ч.

1.3.23. Определить допустимую силу тока и необходимый расход воды для медной круглой шины длиной l=5 м, если известно, что внутренний диаметр шины d_вн=45 мм, наружный d_нap=50 мм, температура воды на входе ϑ_вх=25°С, а допустимая температура воды на выходе ϑ_вых=55°С. Температура внутренней стенки шины не должна превышать ϑ_доп=90°С.

1.3.24. Определить допустимую силу тока и температуру воды на выходе из алюминиевой трубы длиной l=3 м. Расход охлаждающей воды Q=14,5 л/с. Максимальная температура внутренней стенки не выше ϑ_доп=90°С, температура воды на входе ϑ_вх=35°C, внутренний диаметр трубы d_вн=45 мм, внешний dнар = 50 мм.

1.3.25. Определить допустимый ток и температуру воды на выходе для трубчатой медной шины, охлаждаемой водой, протекающей внутри шины со скоростью w = 0,285 м/с. Температура внутренней поверхности трубы не должна превышать ϑ_доп=85°С, температура воды на входе ϑ_вx=25°C, внутренний диаметр шины d_вн=95 мм, наружный d_нар=150 мм, длина шины l=4 м.

1.4. Расчет теплоотдачи излучением и конвекцией

В данном параграфе приведены задачи по расчету теплоотдачи излучением для случаев теплообмена между двумя телами по формулам, вытекающим из закона Стефана - Больцмана, а также задачи, в которых теплоотдача происходит совместно излучением и конвекцией. В ряде случаев, встречающихся в электрических аппаратах, теплоотдача излучением может быть равна или даже больше теплоотдачи конвекцией.

При решении задач данного параграфа используются следующие расчетные формулы и соотношения.

Количество теплоты, которое отдается излучением с 1 м² поверхности (тепловой поток) более нагретого тела менее нагретому телу, в случае, когда одно тело заключено внутри другого,

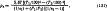
где T₁ и T₂ - соответственно температуры тел, К; ε₁ и ε₂ - степень черноты полного излучения тел; F₁ и F₂ - поверхность тел, м².

Для случая, когда тело находится на достаточном удалении от других тел (в окружающей среде с температурой Т₀, К) тепловой поток излучением с его поверхности

Для двух ограниченных поверхностей, находящихся на близком расстоянии (т.е. когда F₁≈F₂), тепловой поток

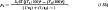
В случае теплообмена между двумя телами, находящихся на некотором расстоянии друг от друга, тепловой поток с поверхности более нагретого тела; передаваемый излучением менее нагретому телу [11],

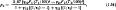
где φ₁₂ и φ₂₁ - средние значения угловых коэффициентов лучистого теплообмена между первым - вторым и вторым - первым телами соответственно, причем

где F₁ и F₂ - поверхность первого и второго тел соответственно, между которыми происходит теплообмен излучением.

1.4.1. Рассчитать наибольший ток, который можно пропустить по катушке электромагнита переменного тока промышленной частоты. Катушка имеет N=1500 витков и намотана на магнитопровод, выполненный из листовой электротехнической стали марки 1511 толщиной листов δ = 0,35 мм. Сталь магнитопровода имеет плотный блестящий слой окиси, электромагнит расположен в камере с глубоким вакуумом. Стенки камеры находятся на достаточном удалении от электромагнита и имеют температуру ϑ₀=35°С. По техническим условиям температура поверхности магнитопровода не может быть выше ϑ=100°С. Размеры магнитопровода приведены на рис. 1.2, где H=150 мм, l=60 мм, l_cр = 360 мм, с=75 м, B=100 мм, а = 35 м, b = 70 мм.

Решение. Так как электромагнит находится в вакууме, то теплоотдача от его поверхности к поверхности вакуумной камеры осуществляется излучением. Так как стенки вакуумной камеры достаточно удалены от электромагнита, то можно предположить, что поверхность камеры значительно больше поверхности магнитопровода. Определим, какое количество теплоты передается с поверхности F магнитопровода, не занятой катушкой, к стенкам камеры, используя формулу (1.52)

При вычислении поверхности магнитопровода, принимающей участие в теплообмене, поверхность магнитопровода, не занятую катушкой, уменьшим примерно на 40%, поскольку часть тепловых лучей, исходящих из поверхности магнитопровода, будет падать на катушку, поглощаться в ней и не достигнет поверхности стенок камеры:

Для условия задачи ε = 0,82 (см. табл. П.12). Тогда

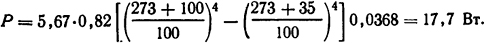
Таким образом, в каждом килограмме магнитопровода может быть выделено теплоты

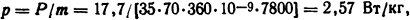
где m - масса магнитопровода.

Для данных задачи потери p = 2,57 Вт/кг будут иметь место при В = 1,3 Тл (см. табл. П.8). Для стали 1511 индукция B=1,3 Тл будет иметь место при напряженности магнитного поля H=1000 А/м. Тогда из уравнения IN=Hl_ср определяем максимально допустимый ток

Ответ: I_доп = 0,24 А.

1.4.2. Определить количество теплоты, которое передается излучением с поверхности одного метра алюминиевой шины круглого поперечного сечения диаметром d=25 мм. Шина расположена в спокойном воздухе, температура которого ϑ₀=35°С, на большом удалении от других тел. Поверхность шины шероховата, а ее температура в результате протекания переменного тока ϑ=95°С.

1.4.3. Решить задачу 1.4.2 при условии, что шина в одном случае полирована, а в другом случае окрашена масляной краской.

1.4.4. Для условий задачи 1.4.1 определить максимально допустимый ток в катушке, если магнитопровод выполнен из сплошного бруска вальцованной стали. Для решения задачи использовать формулу (1.7).

1.4.5. Определить коэффициент теплоотдачи излучением с поверхности медной окисленной шины, если поверхность шины в результате протекания по ней тока нагрета до температуры ϑ=95°С и находится в воздухе, температура которого ϑ₀ = 35°С, на достаточном удалении от других тел.

1.4.6. Найти коэффициент теплоотдачи излучением с поверхности медной круглой шины диаметром d=40 мм, если она заключена в стальную трубу, внутренний диаметр которой d_вн= 2 дюйма, наружный d_нар=60 мм. Поверхности шины и трубы окислены и нагреты соответственно до температур ϑ_ш = 95°С, ϑ_тр=35°С.

1.4.7. Определить допустимую плотность тока в медной круглой шине диаметром d=20 мм, расположенной концентрично в стальной трубе, размеры которой d_вн = 1 дюйм и d_нар=33,5 мм. Между поверхностью шины и трубы - глубокий вакуум. Максимальная температура поверхности шины по техническим условиям не должна быть выше ϑ=100°С, а температура внутренней поверхности "стальной трубы ϑ_тр = 35°С. Поверхность трубы покрыта белым лаком, поверхность шины - черным матовым.

1.4.8. Методом подбора определить температуру поверхности медной круглой шины, которая находится в стальной трубе и пс ней протекает переменный ток I=1000 А частоты f=50 Гц. Температура внутренней поверхности трубы ϑ_тр = 35°С, а между шиной и трубой глубокий вакуум. Поверхность шины окислена, а внутренняя поверхность трубы окрашена белым эмалевым лаком. Диаметр шины d=30 мм, внутренний диаметр трубы ϑ_тр = 1,5 дюйма.

1.4.9. Определить количество теплоты, передаваемое излучением с поверхности цилиндрической катушки индуктивности, имеющей наружный диаметр D_нар=160 мм, внутренний D_ВН = 100 мм, высоту h=170 мм. В результате протекания по катушке тока ее поверхность нагрелась до температуры ϑ=100°С. Катушка заключена в стальную кубическую коробку, высота ребра которой 200 мм. Поверхность катушки покрыта масляной краской. Сталь, из которой изготовлена коробка, оцинкованная блестящая; температура поверхности коробки ϑ_кор=65°С.

1.4.10. Вычислить методом подбора температуру поверхности цилиндрической катушки индуктивности, геометрические размеры которой приведены в задаче 1.4.9. Катушка помещена в замкнутый герметический кубический корпус, высота ребра которого h=250 мм. В корпусе поддерживается глубокий вакуум. Катушка имеет 250 витков из медного круглого провода диаметром d=4 мм, ток, протекающий через катушку, I=10 А. Поверхность катушки покрыта алюминиевой краской, а корпус изготовлен из листовой оцинкованной окисленной стали и его температура ϑ_кор=35°С. Степень черноты излучения для алюминиевой краски ε=0,5.

1.4.11. Определить, какое количество теплоты передается излучением в установившемся режиме теплообмена от нагретой шины к холодной, если шины размером 120×10 мм расположены параллельно друг другу на расстоянии δ = 20 мм. Шина, по которой протекает переменный ток, нагревается до температуры ϑ₁ = 120°С. Температура другой шины ϑ₂=35°С. Обе шины медные и окрашены масляной краской.

Решение. Количество теплоты, передающееся излучением от нагретой шины к холодной, определим по формуле (1.54). Рассчитаем теплообмен на длине шин 1=1 м. Учитывая, что F₁φ₁₂=F₂φ₂₁ [см. формулу (1.55)], имеем

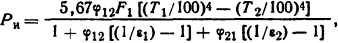
где F₁- теплоотдающая поверхность нагретой шины.

Коэффициент [11]

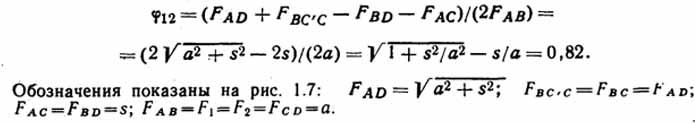
Так как F₁=F₂=120·10^-3 м², то φ₁₂=φ₂₁ = 0,82.

Для масляной краски ε = 0,95.

Тогда

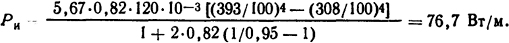
Ответ: Р_и = 76,7 Вт/м.

1.4.12. Определить количество теплоты, передаваемое излучением от медной шины размером 100×8 мм к параллельно расположенной двутавровой балке шириной 120 мм. По шине протекает ток, в результате чего она нагревается до температуры ϑ = 95°С, температура балки ϑ_б = 35°С. Балка окрашена черной масляной краской и находится на расстоянии 10 мм от шины, поверхность которой окислена.

Рис. 1.7. Эскиз расположения шин

1.4.13. Определить коэффициент теплоотдачи конвекцией и излучением с поверхности круглой медной шины, окрашенной масляной краской и имеющей диаметр d=45 мм. Шина находится на достаточном удалении от других частей электроустановки и расположена горизонтально в спокойном воздухе, температура которого ϑ₀ = 35°С. Температура шины ϑ_ш=105°С.

Решение. Общий коэффициент теплоотдачи равен сумме коэффициентов теплоотдачи конвекцией и излучением. Для определения коэффициента теплоотдачи конвекцией воспользуемся формулой (1.38) Nu_m = C[GrPr]_mⁿ, в которой определяющая температура ϑ_m = ( ϑ_ш+ ϑ₀)/2=(105+35)/2=70°С и Рr_m = Рr_с.

При этой температуре для воздуха [см. табл. П.9 и формулу (1.34)]

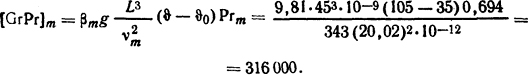
В соответствии с табл. 1.2 С=0,54; n=1/4, следовательно, из формулы (1.33),

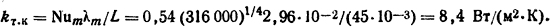
Так как шина находится на достаточном удалении от других частей, то коэффициент теплоотдачи излучением определим с помощью формулы (1.52)

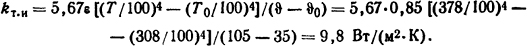
Для масляной краски ε = 0,95. Тогда

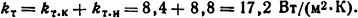
Ответ: k_т=17,2 Вт/(м²·К).

1.4.14. Определить суммарный коэффициент теплоотдачи с поверхности токопровода, изготовленного в виде стальной окрашенной масляной краской трубы, расположенной горизонтально в спокойном воздухе, температура которого ϑ₀ = 35°С. Температура поверхности шины ϑ = 95°С, а ее наружный диаметр d = 60 мм.

1.4.15. Определить допустимый ток, протекающий через низкоомный жидко-металлический реостат, изготовленный в виде двух концентрических труб (рис. 1.8). Внутренняя труба изготовлена из нержавеющей стали, а наружная - из меди. Изменение сопротивления осуществляется изменением уровня жидкого металла между этими трубами. Между трубами поддерживается глубокий вакуум, а внутри внутренней трубы с целью охлаждения пропускают воду со скоростью w = 1 м/с. Температура воды на входе трубы ϑ_вх = 20°С, на выходе ϑ_вых = 60°С, а температура внутренней и наружной труб соответственно 65 и 40°С. Значения степени черноты внутренней трубы ε₁=0,9, наружной ε₂=0,95, удельное сопротивление нержавеющей стали ρ = 0,9·10^-6 Ом·м.

Решение. Определим мощности, которые будут передаваться от нагретой внутренней трубы воде и окружающему воздуху.

Средняя температура воды в трубе

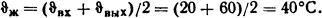
При этом параметры жидкости следующие:

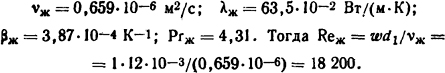
Так как для Re>10000 движение в трубе турбулентно, то используем критериальное уравнение (1.49):

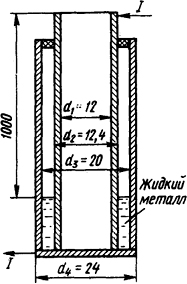
Рис. 1.8. Эскиз низкоомного реостата

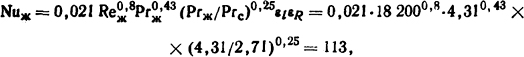
где Рr_с = 2,71 - значение Прандтля при ϑ_c=65°С, а ε_l = ε_R = 1.

Коэффициент теплоотдачи от внутренней поверхности трубы воде определим по формуле (1.33)

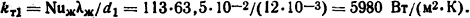
Таким образом, с внутренней поверхности трубы отдается количестве теплоты

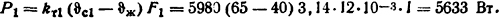
Количество теплоты, отдаваемое трубой из нержавеющей стали медной трубе, определим из формулы (1.51)

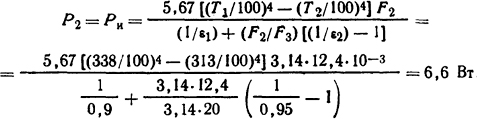
Здесь F₁=3,14·12·10^-3·1 м²; F₂ = 3,14·12,4·10^-3·1 м²; F₃ = 3,14·20·10^-3 м². Полная мощность, которая может быть отведена от трубы из нержавеющей стали, Ρ=Ρ₁+P₂=5633+6,6=5639,6 Вт. Допустимый ток, который можно пропустить через реостат