Простейшие методы расчета нагрева я охлаждения электрических аппаратов и их частей 2 страница

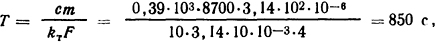
где с - удельная теплоемкость меди; γV=m - масса стержня длиной в 1 м; γ - плотность меди; V - объем проводника; F - охлаждающая поверхность

Таким образом, уравнение кривой нагрева Θ=114 (1 - е^-t/850).

Ответ: Θ=114 (1 - е^-t/850).

1.2.2. Написать уравнение кривой охлаждения медного стержня для условий задачи 1.2.1, если известно, что ток был выключен через 40 мин после начала нагрева.

1.2.3. Определить постоянную времени нагрева и построить кривую нагрева стальной шины прямоугольного сечения 90×4 мм, если по ней протекает ток I=500 А, шина расположена в спокойном воздухе, температура которого ϑ₀=35°С, а коэффициент теплоотдачи с поверхности шины k_т=15 Вт/(м²·К). Удельное сопротивление стали принять ρ= 12·10^-8 Ом·м.

1.2.4. Определить постоянную времени нагрева цилиндрической катушки постоянного тока, которая намотана круглым медным проводом диаметром d=2 мм, имеет 500 витков, ее внутренний диаметр D_вн= 70 мм, наружный D_нар=140мм, высота h = 70 мм. Теплоотдача в окружающую среду, которой является спокойный воздух, осуществляется с боковых поверхностей и с торцов, коэффициент теплоотдачи k_т = 20 Вт/(м²·К).

1.2.5. Написать уравнение кривой нагрева медного круглого проводника диаметром d = 40 мм с учетом изменения удельного сопротивления его от температуры, если в момент времени t = 0 он нагружается током I=2250 А. Проводник расположен в спокойном воздухе, температура которого ϑ₀=35°С, а коэффициент теплоотдачи с наружной поверхности k_т=16 Вт/(м²·К).

Решение. Постоянная времени нагрева определится из формулы (1.21). Для длины проводника l=1 м, поскольку С=с·m, где с - удельная теплоемкость материала, m - масса проводника, m=γSl=γS, S - поперечное сечение

проводника, γ - плотность, a P₀=I²ρ₀l/S, где ρ₀ - удельное сопротивление материала проводника при 0°С, будем иметь

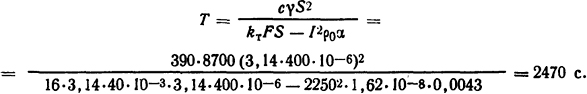
Установившаяся температура с учетом указанных замечаний определится из формулы (1.20), т.е.

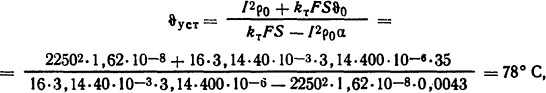
где ρ₀= 1,62·10^-8 Ом·м; α=0,0043 K^-1.

Поскольку ϑ_н= ϑ₀, ϑ_уст=Θ_уст+ ϑ₀, ϑ = Θ+ ϑ₀, из формулы (1.19) уравнение кривой нагрева получаем в виде

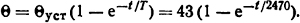
Ответ: Θ=43 (1-е^-t/2470).

1.2.6. Составить уравнение кривой нагрева алюминиевой шины прямоугольного поперечного сечения 100×10 мм, если в момент времени t=0 она нагружается постоянным током I=2000 А. В начальный момент времени температура шины ϑ_н=50°С, температура окружающего воздуха ϑ₀=35°С, коэффициент теплоотдачи с наружной поверхности шины k_т=20 Вт/(м²·К). При расчете учесть изменение удельного сопротивления алюминия от температуры.

1.2.7. Вычислить время, через которое медная труба с поперечными размерами d_вн=25 MM, d_нap=30 мм нагреется до температуры ϑ=110°С в результате протекания тока I=9400 А. C целью охлаждения по трубе протекает вода, средняя температура которой ϑ_ср=40°С. Коэффициент теплоотдачи с внутренней поверхности трубы k_т=1500 Вт/(м²·К). Удельное сопротивление меди ρ=1,75·10^-8 Ом·м.

1.2.8. Решить задачу 1.2.7 при условии, что шина охлаждается не водой, а находится в спокойном воздухе, температура которого ϑ₀=40°C, коэффициент теплоотдачи с ее наружной поверхности k_т=15 Вт/(м²·К). Остальные данные без изменения.

1.2.9. Определить время, через которое медная шина с размерами поперечного сечения 100x6 мм нагреется переменным током I=5000 А до температуры ϑ=100°С, если она находится в спокойном воздухе с температурой ϑ₀=35°С, коэффициент теплоотдачи с наружной поверхности шины k_т = 15 Вт/(м²·К), а начальная температура шины ϑ_н=50°С.

1.2.10. Определить допустимое число включений в 1 ч катушки постоянного тока в повторно-кратковременном режиме нагрева, если время рабочего периода катушки t_р=150 с и по ней протекает

ток I_пк=12 А. Катушка цилиндрическая, намотана круглым медным проводом диаметром d=2 мм, имеет 500 витков, ее внутренний диаметр D_вн=70 мм, наружный D_нар=140 мм, высота катушки h = 70 мм. Катушка находится в спокойном воздухе, температура которого ϑ₀=35°C. С наружных поверхностей катушки коэффициент теплоотдачи k_т = 20 Вт/(м²·К). Изоляция провода хлопчатобумажная без пропитки.

Решение. Длительно допустимая величина тока определится из равенства

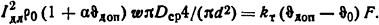
Для хлопчатобумажной изоляции ϑ_доп = 90°С. Подставляя числовые значения и производя вычисления, получим I_дл=8 А. Тогда коэффициенты перегрузки по току k_I=I_пк/I_дл = 12/8 =1,5 и мощности k_P = k_I²=2,25.

Постоянную времени нагрева катушки определим, исходя из предположения, что способностью воспринимать теплоту обладают только ее токопроводящие элементы:

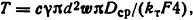
где с, γ - соответственно удельная теплоемкость вычисления получим T=1400 с.

Тогда из равенства и плотность меди. После

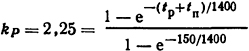
найдем время одного цикла t_ц=t_р+t_п=372 с.

Допустимое число включений катушки в час n=3600/t_ц=3600/372 = 9,7 ≈ 9.

Ответ: n=9.

1.2.11. Определить допустимое число включений электромагнита постоянного тока, который имеет цилиндрическую катушку, намотанную круглым медным проводом диаметром d=4 мм. Катушка

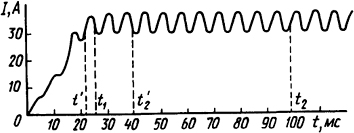
Рис. 1.4. Осцилограмма тока при включении электромагнита

имеет 250 витков, ее наружный диаметр D_нар=160 мм, внутренний D_вн=100 мм, высота h=170 мм; питается она выпрямленным током, нарастающим по закону, приведенному на рис. 1.4. Электромагнит включается в момент времени t₁ = 25 мс, а выключается автоматически в момент времени t₂=t₁+75 мс. Длительно допустимая температура нагрева катушки, витки которой

имеют хлопчатобумажную изоляцию, ϑ_доп=90°С. Катушка находится в спокойном воздухе, температура которого ϑ₀=35°C, коэффициент теплоотдачи с поверхности катушки k_т = = 10 Вт/(м·К). В теплоотдаче принимают участие наружная боковая поверхность и торцы катушки. Внутренняя поверхность катушки теплоизолирована.

Решение. Определим эквивалентный по теплоте ток:

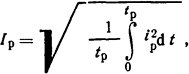
где t_p=t₂=100 мс - время рабочего периода; i_p - мгновенное значение тока.

Если в пределах от 0 до t’₁=22 мс кривую тока представить в виде i_p1=2t, а от t’₁ до t₂=100 мс в виде t_p2= 44+4 sin ωt, где ω=2πf, то

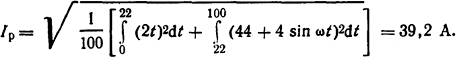
Длительно допустимое значение тока через катушку определим из равенства

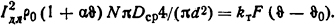
Подставив числовые значения, получим I_дл=22 А. Коэффициент перегрузки по току k_I=I_P/I_дл=39,2/22=1,78. Очевидно, t_p+t_п≪T и, следовательно, справедливо соотношение 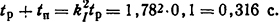, откуда

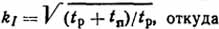
Тогда число допустимых включений в час n= 3600/0,316= 11400.

Ответ: n=11400.

1.2.12. Определить значение коэффициентов перегрузки по мощности и току стальной шины прямоугольного сечения 100×4 мм, нагреваемой прерывистым током I=600 А через установленные промежутки времени. Допустимая температура нагрева шины ϑ_доп=95°С. Шина находится в спокойном воздухе, температура которого ϑ₀=35°С, коэффициент теплоотдачи с поверхности шины k_т=12 Вт/(м²·К), температура шины в результате протекания прерывистого тока достигает ϑ=95°C.

1.2.13. Решить задачу 1.2.11 при условии, что автоматическое устройство выключает катушку в момент времени t’₂ = 40 мс. Все остальные данные без изменения.

1.2.14. Найти конечную температуру медного круглого проводника диаметром d=20,0 мм, который в течение 1,5 с нагружается током I=32000 А, если в начальный момент времени проводник находился в спокойном воздухе при температуре ϑ_н=0°C, а коэффициент теплоотдачи с его поверхности k_т=17 Вт/(м²·К).

Решение. Постоянная времени нагрева проводника длиной в 1 м из формулы (1.22) T=cγS/(k_тF) = 1000 с. Поскольку t/T=1,5·10^-5<0,1, процесс

нагрева можно считать адиабатическим и температуру проводника определить по кривой адиабатического нагрева для меди (см. рис. П.8).

Для данного случая

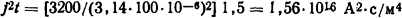
и, следовательно, ϑ_кон=80°C.

Ответ: ϑ_кон=80°C.

1.2.15. Определить температуру алюминиевой шины прямоугольного сечения размером 40×5 мм после протекания по ней тока I = 20000 А в течение времени t=1 с. Начальная температура шины ϑ_н=0°С.

1.2.16. Решить задачу 1.2.14 при условии, что в начальный момент времени проводник был нагрет до температуры ϑ_н=80°0, а все остальные данные оставлены без изменения.

Решение. Для температуры ϑ_н=80°С квадратичный импульс плотности тока (по кривой адиабатического нагрева для меди, см. рис. П.8) [j²t]_н = 1,56·10¹⁶ А²·с/м⁴. Следовательно, конечное значение импульса плотности тока [j²t]_кон=[j²t]_нач[j²t]= 1,56·10¹⁶+1,56·10¹⁶=3,12·10¹⁶ А²·с/м⁴.

По кривой адиабатического нагрева (см. рис. П.8) для [j²t]_кон находим ϑ_кон = 200°C.

Ответ: ϑ_кон = 200°C.

1.2.17. Определить необходимый диаметр поперечного сечения круглой проволоки нихромового элемента сопротивления реостата, если известно, что в момент времени, когда элемент сопротивления нагрет до температуры ϑ=100°С, через него в течение времени t=2 с протекает ток I= 100 А. Допустимая температура нагрева нихрома в кратковременном режиме ϑ_доп=450⁰С.

Решение. Суммарный квадратичный импульс плотности тока для нихрома при ϑ_доп = 450°С (см. рис. П.9) будет [j²t]_кон=1,4·10¹⁵ А²·с/м⁴; при ϑ_нач=100°С имеем [j²t]_нач=0,32·10¹⁵ А²·с/м⁴.

Допустимый квадратичный импульс плотности тока [j²t]_доп=[j²t]_кон-[j²t]_нач=1,4·10¹⁵- 0,32·10¹⁵= 1,08·10¹⁵ А²·с/м⁴.

Необходимый диаметр поперечного сечения

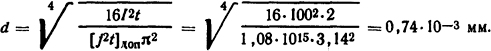
Ответ: d=0,74 мм.

1.2.18. Определить необходимый диаметр константановой проволоки элемента сопротивления пускового реостата, если известно, что при начальной температуре сопротивления ϑ_н=50°С элемент сопротивления в течение одной секунды нагружается током I=50 А. Для константана допустимая температура в кратковременном режиме ϑ_доп=200°C.

1.2.19. Подобрать стандартную алюминиевую шину прямоугольного сечения для распределительного устройства, в котором возможные токи трехфазного к.з. имеют длительность t_к.з=10 с. Шина должна выдерживать токи к.з., установившиеся значения которых I_∞ = 30000 А, а начальные пиковые I _р = 75000 А. Расчет произвести для случая, когда шина в результате протекания

номинального тока была нагрета до температуры ϑ_нач=80°С. Охлаждение шины естественное воздушное.

Решение. Определим фиктивное время к.з. по рис. П.10. Поскольку t_к.з>5 с, будем считать, что после 5 с ток к.з. равен установившемуся току. Тогда полное фиктивное время к.з. t_ф = t’_ф+(t_к.з-5), где t'_ф - фиктивное время к.з. при t_к.з = 5 с.

Для данной задачи при β" = I_≈p/I_∞ =2,5 и t’_к.з. = 5 с имеем t’_ф = 6 с. Тогда t_ф=6+ (10-5) = 11 с.

Максимально допустимая температура за время к.з. для алюминия ϑ_доп = 200°С При этой температуре [j²t]_кон=1,35·10¹⁶ А²·с/м⁴. Для ϑ_нач = 80°С имеем [j²t]_нач = 0,75·10¹⁶ А²·с/м⁴. Тогда

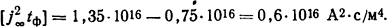
Требуемое поперечное сечение шины определим из равенства

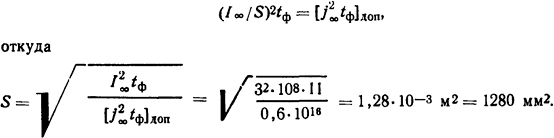
Этой площади будут соответствовать две шины с размерами поперечного сечения 80×8 мм.

Ответ: две шины 80×8 мм.

1.2.20. Определить температуру нагрева медной прямоугольной шины с размерами поперечного сечения 80×10 мм в результате протекания по ней в течение 8 с тока к.з. с параметрами I_≈р=90000 А, I_∞ = 40000 А, если известно, что в начальный момент к.з. по Шине протекал номинальный ток и температура шины при этом составляла ϑ_нач=90°С. Шина находится в спокойном воздухе.

1.2.21. Определить ток десятисекундной термической стойкости для стальной шины прямоугольного сечения размером 100×4 мм, находящейся в спокойном воздухе, для случая, когда начальная температура шины ϑ_нач=80°С. Для стальной шины допустимая температура в кратковременном режиме нагрева ϑ_доп=300°С.

1.3. Расчет теплоотдачи конвекцией с поверхностей электрических аппаратов

В данном параграфе приведены задачи на определение коэффициентов теплоотдачи с использованием известных критериальных уравнений для случаев свободной и вынужденной конвекции для различных частей электрических аппаратов, в которых применяются жидкости и газы в качестве охлаждающей среды.

Количество теплоты, отдающееся с поверхностей нагретых частей электрических аппаратов, в основном зависит от условий конвективного теплообмена, поэтому большое значение имеет умение правильно рассчитать количество

теплоты, отводимого конвекцией. Для этой цели используют критериальные уравнения, полученные на основе рассмотрения подобных явлений.

Для решения задач данного параграфа используются следующие расчетные формулы и соотношения.

Критериальное уравнение конвективной теплоотдачи в общем виде

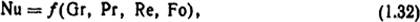
где Nu, Gr, Pr, Re и Fo - соответственно критерии Нуссельта, Грасгофа, Прандтля, Рейнольдса и Фурье:

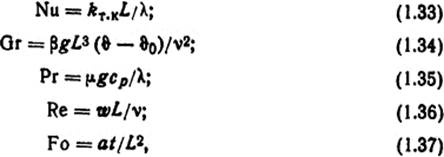
где k_т.к - коэффициент теплоотдачи конвекцией, Вт/(м²·К); L - характерный геометрический размер, м; λ - коэффициент теплопроводности, Вт/(м·К); В -коэффициент объемного расширения, Κ^-1; ϑ - температура поверхности, С; ϑ₀ - температура окружающей среды, °С; ν -кинематическая вязкость жидкости или газа, м²/с; μ - динамическая вязкость жидкости или газа, Н·с/м²; g - ускорение силы тяжести, м/с²; с_p - удельная теплоемкость жидкости или газа при постоянном давлении, Дж/(кг·К); w - скорость, м/с; а - коэффициент температуропроводности, м²/с; t - время, с.

Критериальное уравнение для свободной конвекции в неограниченном пространстве [1]

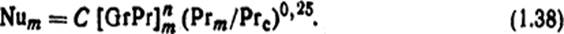
Индекс у критерия подобия обозначает, что при вычислениях соответствующего критерия физические параметры необходимо вычислять при температуре с тем же индексом.

ϑ_c - температура поверхности тела.

Величины С и n определяются по табл. 1.2 [1].

Примечание. При использовании формулы (1.38) для горизонтальных плит полученный коэффициент теплоотдачи необходимо увеличить да 30% для верхней плоскости плиты и уменьшить на 30% для нижней плоскости.

При расчете конвективного теплообмена в ограниченном пространстве (стесненная конвекция) тепловой поток теплоотдачи [1]

где ϑ₁, ϑ₂ - температуры поверхностей, принимающих участие в теплообмене,

°С; δ - характерный линейный размер (расстояние между поверхностями), м; λ_эк - эквивалентный коэффициент теплопроводности, Вт/(м·К).

где λ - коэффициент теплопроводности при определенной температуре, Вт/ (м· К); ε_к - коэффициент конвекции.

Величины A и r определяются из табл. 1.3.

Критериальные уравнения вынужденной конвекции теплоотдачи при поперечном обтекании одиночного цилиндра [11]:

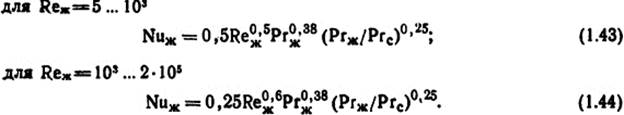
Величины ϑ_ж - средняя температура жидкости или газа, °С, ϑ_с -температура поверхности цилиндра, °С.

Критериальные уравнения вынужденной конвекции при движении жидкости вдоль плоской стенки [11]:

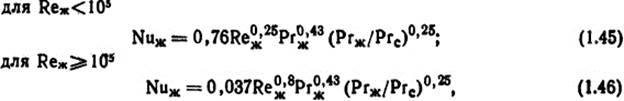
где ϑ_ж - температура в начале стенки по отношению к набегающему потоку, °С; ϑ_с - средняя температура поверхности стенки, определяющим размером является длина стенки.

Критериальные уравнения конвективной теплоотдачи при протекании жидкости или газа в гладких трубах (кроме жидких металлов) [11]:

для Re_ж≤2200 (ламинарное движение)

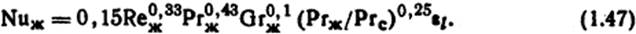
ϑ_ж и ϑ_с - соответственно средние значения температур жидкости или газа я поверхности трубы, °С;

где ϑ_вх и ϑ_вых - соответственно температуры жидкости или газа на входе в трубу и на выходе из нее, °С.

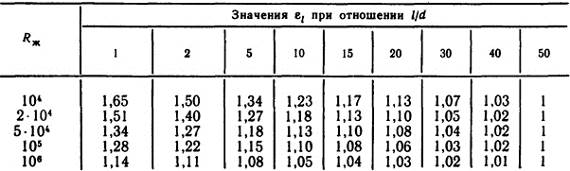
Таблица 1.4

Определяющим размером является внутренний диаметр трубы, а коэффициент ε_l определяется из табл. 1.4, в которой l/d - отношение длины трубы к ее внутреннему диаметру.

Для Re>10000 (турбулентное движение)

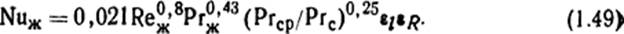
Величины ϑ_ж, ϑ_с и определяющий размер те же, что и для выражения (1.47)

где d - внутренний диаметр трубы, м; R - радиус закругления трубы.

Значение ε_l определяется из табл. 1.5.

Таблица 1.5

1.3.1. Определить коэффициент теплоотдачи конвекцией с боковой наружной поверхности цилиндрической катушки индуктивности высотой h = 200 мм, расположенной вертикально в спокойном воздухе, температура которого ϑ₀=35°С. Катушка достаточно удалена от других аппаратов и устройств В результате протекания по ней тока температура ее поверхности ϑ=105°С.

Решение. Из условий задачи следует, что имеет место свободная конвекция в неограниченном пространстве и, следовательно, для определения коэффициента теплоотдачи конвекцией можно воспользоваться формулой. (1.38). Так как для воздуха Pr_m≈Pr_c, то

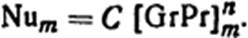
Для определения коэффициентов С и n необходимо вычислить произведение [GrPr] при ϑ_m=( ϑ_н- ϑ₀)/2=(105+35)/2 = 70°C.

Значение физических параметров воздуха при температуре ϑ_m = 70°С (см. табл. П.9): ν_m = 20,02·10^-6 м²/с; λ_m = 2,96·10^-2 Вт/(м·К); Pr_m = 0,694; Gr_m = β_mg( ϑ- ϑ₀)L³/ν_m²; для воздуха β_m = 1/(273+ ϑ_m) = (1/(273+70) = 1/343 К^-1; g=9,81 м/с.

В качестве определяющего размера примем высоту катушки h=L=0,2 м. Таким образом, используя формулу (1.34),

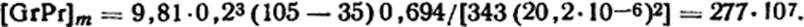
Из табл. 1.2 определяем С=0,135; n=1/3. Тогда Nu_m=0,135(2,77·10⁷)^1/3 =40,8, откуда из формулы (1.33) k_т.к = 40,7·2,96·10^-2/0,2=6,04 Вт/(м²·К).

Ответ: k_т.к=6,04 Вт/(м²·К).

1.3.2. Решить задачу 1.3.1 при условии, что высота катушки h = 300 мм.

1.3.3. Определить коэффициент теплоотдачи от вертикальной стенки высотой h = 2 м окружающему воздуху, если температура стенки ϑ=80°C. Стенка находится в спокойном воздухе, температура которого ϑ₀ = 35°С.

1.3.4. Определить коэффициент теплоотдачи с поверхности цилиндрического проводника, расположенного горизонтально в спокойном трансформаторном масле, температура которого ϑ₀ = 20°С. Температура поверхности проводника ϑ_c = 75°С, диаметр d=45,0 мм.

1.3.5. Вычислить коэффициент теплоотдачи от трансформаторного масла, нагретого до температуры ϑ₀=75°С, в который поместили горизонтально круглую шину. Диаметр шины d = 45 мм, начальная температура ϑ_c=20°С.

1.3.6. Определить, во сколько раз изменится коэффициент теплоотдачи конвекцией с поверхности круглого проводника диаметром d=10 мм воде и трансформаторному маслу по сравнению со спокойным воздухом, если температура поверхности 90°С, а охлаждающей среды 35°С для всех случаев.

1.3.7. Определить эквивалентный коэффициент теплопроводности и плотность теплового потока между двумя вертикальными плоскими стенками, находящимися друг от друга на расстоянии δ=10 мм, если известно, что температуры стенок соответственно ϑ₁ = 150°C, ϑ₂=35 °С, а между стенками находится спокойный воздух.

Решение. Воспользуемся для стесненной конвекции уравнением (1.40), в котором определяющая температура из формулы (1.42) будет равна

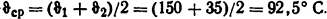
При этой температуре параметры воздуха будут следующие (см. табл. П.9): β_ср= 1/366 К^-1; ν_cp=22,4·10^-6 м²/с; λ_ср=3,15·10^-2 Вт/(м·К); Рr_ср=0,690. Тогда, используя формулу (1.34),

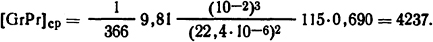
В этом случае справедливо критериальное уравнение (1.41), где А = 0,105 и r=0,3 (см. табл. 1.3), т.е. ε_к=0,105·4237^0,3=1,29. Эквивалентный коэффициент теплопроводности λ_эк = ε_кλ= 1,29·3,15·10^-2=4,05·10^-2 Вт/(м·К). Из закона теплопроводности Фурье определим плотность теплового потока:

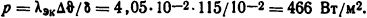
Ответ: λ_эк = 4,05·10^-2 Вт/(м·К); р=466 Вт/м².

1.3.8. Определить значение теплового потока в зазоре δ = 3 мм между двумя трубами длиной l=1 м, если диаметр внутренней трубы равен d=30 мм, между трубами находится трансформаторное масло, а температуры поверхностей труб равны соответственно ϑ₁=80°С, ϑ₂=35°С.

1.3.9. Вычислить коэффицент теплоотдачи с поверхности медного круглого шинопровода диаметром d= 15 мм, а также допустимую силу постоянного тока, если известно, что шинопровод охлаждается поперечным потоком сухого воздуха при скорости обдува w = 1 м/с. Температура поверхности шинопровода ϑ_ш=80°С, а температура воздуха ϑ₀=20°C.

Решение. Приняв для воздуха Рг≈0,7, можно упростить формулы (1.43) и (1.44), при этом

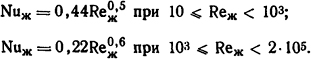
В качестве определяющей температуры принимаем среднюю температуру потока воздуха, а в качестве характерного размера - диаметр шинопровода. Для ϑ_ж=20°С из табл. П.9 и формулы (1.36) получаем

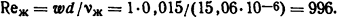
Тогда Nu_ж = 0,44·996^0,5= 13,9 и, следовательно, из формулы (1.33) получаем

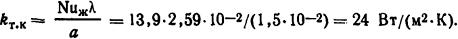
Из соотношения 4I²ρ₀(1 + α ϑ)l/(πd²)=k_т.к( ϑ_ш- ϑ₀)πdl получаем

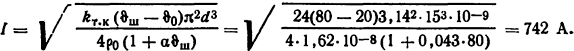
Ответ: I=742 А.

1.3.10. Определить наибольшую силу тока, пропущенного через электрический нагреватель из нихромовой проволоки диаметром d=1,0 мм, допустимая температура нагрева которой ϑ_доп=1000°С. Нагреватель находится в спокойном воздухе, температура которого ϑ₀=10°С, а конструкция нагревателя такова, что его можно рассчитывать как одиночный цилиндр. Теплоотдачей излучением пренебречь.