Простейшие методы расчета нагрева я охлаждения электрических аппаратов и их частей 1 страница

В данном параграфе приведены задачи по определению мощности источников теплоты: джоулева тепла, потерь от поверхностного эффекта, эффекта близости, тепловыделения в ферромагнитных нетоковедущих частях, находящихся в переменном магнитном поле, а также те задачи по расчету теплоотдачи с поверхностей нагретых тел, для решения которых необходимо использовать формулу Ньютона и эмпирические формулы коэффициентов теплоотдачи для простейших, наиболее распространенных в электрических аппаратах поверхностей охлаждения. При этом используются следующие расчетные формулы и соотношения.

Количество теплоты, выделяемое в неоднородном проводнике объемом V за отрезок времени Δt=t₂-t₁ при неравномерном распределении плотности тока j в нем, равно

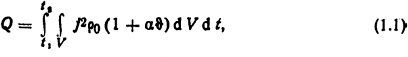
где ρ₀, α - удельное сопротивление, Ом·м, и температурный коэффициент сопротивления, 1/°С, материала проводника при 0°С соответственно; ϑ - температура проводника, °С.

Мощность источников теплоты для однородных проводников при переменном токе можно определить по упрощенной формуле

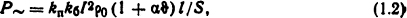
где k_п и k_б - соответственно коэффициенты поверхностного эффекта и эффекта близости, которые для неферроиагнитных проводников определяют по графикам, приведенным в приложении (см. рис. П.1- П.5); l и S - длина, м, и площадь поперечного сечения, м², проводника соответственно.

Для проводников яз ферромагнитного материала

где S, Π - площадь, м², и периметр поперечного сечения, м, проводника соответственно; z_a - глубина проникновения электромагнитной волны, м

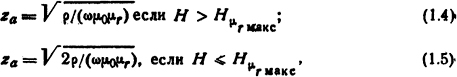
где ω - угловая частота переменного поля; μ₀ - магнитная постоянная (μ₀=4π·10^-7 Гн/м); μ_r - относительная магнитная проницаемость; H - напряженность магнитного поля, Гн/м; Н_{μr макс} - амплитуда первой гармоники напряженности магнитного поля, Гн/м, соответствующая максимуму μ_r на кривой намагничивания материала [1].

Для упрощенных расчетов мощность источников теплоты в ферромагнитных проводниках при переменном токе определяют по формуле [1]

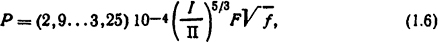
где F и Π - соответственно боковая поверхность, м², и периметр поперечного сечения, м, проводника; f - частота переменного тока, Гц.

Мощность источников теплоты в ферромагнитных нетоковедущих частях, находящихся в переменном магнитном поле, определяют:

- для замкнутого сплошного магнитопровода, на котором надета катушка,

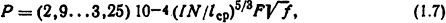
где IN - магнитодвижущая сила катушки, А; l_ср - длина средней магнитной силовой линии, м; F - боковая поверхность магнитопровода, м².

Для практических расчетов рекомендуется принимать среднее значение числового коэффициента:

- для замкнутого шихтованного магнитопровода

где р_уд - удельные потери, определяемые по графикам приложения (см. рис. П.6 и П.7) ; m - масса магнитопровода;

- для ферромагнитного кольца, охватывающего проводник с током I,

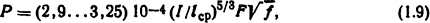
где l_ср - длина средней магнитной силовой линии, м; F - поверхность кольца, м²;

- для единицы длины ферромагнитной полосы (балки), расположенной перпендикулярно проводнику с током I [2],

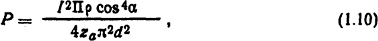
где α - угол между вектором напряженности магнитного поля в данной точке и его составляющей вдоль продольной оси полосы; Π - периметр поперечного сечения, м; ρ - удельное сопротивление материала полосы, Ом·м; а - минимальное расстояние между осями проводника с током я полосы, м.

Мощность источников теплоты в электрической изоляции, находящейся в переменном электрическом поле [1],

где ω - угловая частота переменного поля; С - электрическая емкость изолятора, Ф; U - напряжение, приложенное к изолйтору, В; tgδ - тангенс угла диэлектрических потерь.

Количество теплоты, которое отводится с поверхности электрического аппарата в окружающую среду в стационарном режиме, можно определить по формуле Ньютона

где k_т - коэффициент теплоотдачи, Вт/(м²·К), F - охлаждающая поверхность, м²; ϑ и ϑ₀ - температуры поверхности и окружающей среды соответственно, °С.

Для приближенных расчетов коэффициент теплоотдачи определяют по эмпирическим формулам [1]:

- для окрашенной краской прямоугольной шины с размерами поперечного сечения 120×10 мм, находящейся в спокойном воздухе, большая сторона сечения которой расположена вертикально

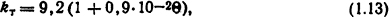
где Θ= ϑ- ϑ₀ - перепад температур;

- для горизонтальных цилиндрических проводников, окрашенных крас кой и расположенных горизонтально в спокойном воздухе,

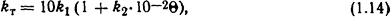
где k₁ и k₂ определяют из табл. 1.1;

Таблица 1.1

- для круглой трубы диаметром d, внутри которой протекает вода со скоростью w [2],

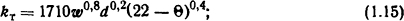
- для цилиндрических катушек в случае, когда охлаждающая поверхность 10^-4<F<10^-2 м²,

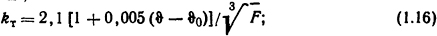
- для цилиндрических катушек, охлаждающая поверхность которых 10^-2<F<0,5 м²,

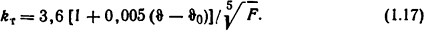
1.1.1. Определить коэффициент поверхностного эффекта для алюминиевого шинопровода, нагретого протекающим по нему переменным током промышленной частоты до температуры ϑ = 95°С, для следующих случаев: а) шинопровод круглый d = 80 мм; б) шинопровод трубчатый с наружным диаметром d_нар=80 мм и с внутренним диаметром d_вн=50 мм; в) шинопровод трубчатый с d_нар = 80 MM, d_вн=74 мм.

Решение. Коэффициент поверхностного эффекта можно определить по графикам, изображенным на рис. П.1 и П.2 приложения. Для этого необходимо вычислить параметр √f/R₁₀₀ где f - частота переменного тока, Гц; R₁₀₀ - активное сопротивление постоянному току проводника длиной /=100 м, Ом.

Для условия (а) данной задачи

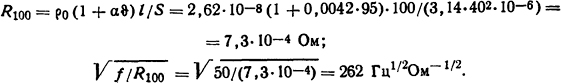
Из графика, изображенного на рис. П.1, k_п = 1,75.

Для условия (б) задачи

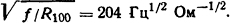
Из графика, изображенного на рис. П.2, k_п=1,1. Для условия (в) задачи

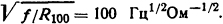
Из графика, изображенного на рис. П.2, k_п = 1,0.

Ответ: а) k_п=1,75; б) k_п=1,1; в) k_п=1,0.

1.1.2. Определить количество теплоты, выделяющейся в одном метре длины медного шинопровода распределительного устройства, по которому протекает ток I=840 А; шинопровод нагрет до температуры ϑ=90°0, его диаметр d=20 мм.

1.1.3. Определить коэффициент поверхностного эффекта и количество теплоты, выделяющейся в одном метре длины круглого шинопровода диаметром d = 45 мм, по которому протекает переменный ток I=2400 А промышленной частоты f=50 Гц. Задачу решить для случаев, когда шинопровод выполнен из алюминия и из меди.

1.1.4. Определить коэффициент поверхностного эффекта и потери электрической энергии в одном метре длины стальной трубчатой шины, имеющей наружный диаметр d_нар=137 MM, a внутренний d_вн=5 дюймов. По шине, температура которой 110°С, протекает ток I=800 А частоты f=50 Гц.

Решение. Для определения потерь энергии в стальной шине воспользуемся формулой Η.Ε. Лысова (1.6), приняв в качестве числового коэффициента максимальную величину, т.е.

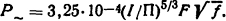
Если охлаждающая поверхность шины (одного метра шины)

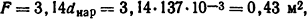
то потери мощности при переменном токе

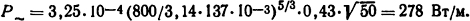
Коэффициент поверхностного эффекта k_п = P_∼/P₌. Здесь P₌ - потери мощности при постоянном токе:

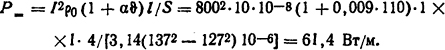
Тогда k_п=278/61,4=4,63.

Ответ: k_п = 4,53; Р_∼=278 Вт/м.

1.1.5. Решить задачу 1.1.4 при условии, что шина изготовлена в виде стальной трубы тех же поперечных размеров, но имеет продольный разрез шириной Δ = 2 мм.

1.1.6. Определить коэффициент поверхностного эффекта и потери энергии в одном метре стальной прямоугольной шины размером 80×4 мм, если по ней протекает переменный ток I=250 А промышленной частоты f=50 Гц и температура шины ϑ=110°С.

1.1.7. Определить коэффициенты поверхностного эффекта и эффекта близости, а также количество теплоты, выделяющейся в одном метре длины шин размером 100×10 мм, если они расположены в одной плоскости на расстоянии 200 мм друг от друга и по ним протекает переменный ток I=1800 А частоты f=50 Гц. Шины выполнены из алюминия и после протекания по ним тока нагрелись до 95°С.

1.1.8. Определить тепловые потери в одном метре длины шины для условий задачи 1.1.7 с той лишь разницей, что шины расположены

не в одной плоскости, а в параллельных плоскостях на расстоянии 50 мм.

1.1.9. Определить тепловые потери в чугунном кольце, охватывающем проводник с током I=2500 А частоты f=50 Гц. Внутренний диаметр кольца D_вн=100 мм, наружный диаметр кольца D_нар=150 мм, его высота h=150 мм.

Решение. Воспользуемся формулой (1.9), приняв в качестве числового коэффициента величину 3,75. В данном случае средняя длина магнитной силовой линии

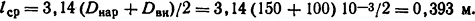
Охлаждающая поверхность

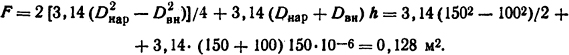
Тогда тепловые потери

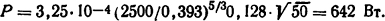
Следует отметить, что полученное значение мощности, выделяемой во фланце, довольно значительно. Необходимо применить специальные меры по его охлаждению или уменьшению потерь во фланце.

Ответ: Р = 642 Вт.

1.1.10. Определить количество теплоты, выделяемое в стальном фланце (рис. 1.1), внутри которого проходит проводник с переменным током I=1000 А частоты f=50 Гц.

1.1.11. Определить количество теплоты, выделяющееся в катушке индуктивности переменного тока, которая намотана на замкнутый магнитопровод, выполненный из горячекатаной

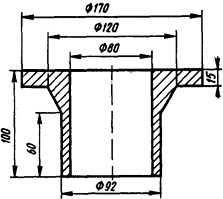
Рис. 1.1. Эскиз стального фланца

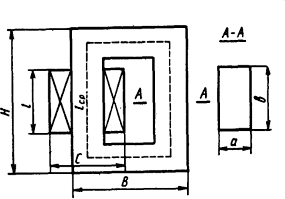
Рис. 1.2. Эскиз магнитопровода с катушкой

трансформаторной листовой стали марки 1511 с толщиной листа δ=0,35 мм. По катушке, имеющей число витков N=1250, протекает переменный ток I=0,6 А частоты f=50 Гц, размеры магнитопровода приведены на рис. 1.2, где а = b = 35 мм, H=130 мм, В = 80 мм, l_cp=280 мм.

Решение. Определим массу m стали в сердечнике. Так как магнитопровод изготовлен из листовой стали, то необходимо учесть коэффициент заполнения поперечного сечения магнитопровода.

Примем k_з=0,9. Тогда m = k_зγV=0,9·7870·35·35·280·10^-9 = 2,43 кг. Здесь γ, V - плотность и объем стали соответственно.

По графику зависимости удельных потерь от магнитной индукции, марки стали и толщины листа определим значение удельных тепловых потерь (см, рис. П.6). Значение магнитной индукции в сердечнике определяем по табл. П.8.

Напряженность магнитного поля

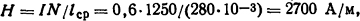
где l_ср - средняя длина магнитной силовой линии. Из табл. П.8 B=1,57 Тл.

В соответствии с рис. П.6 удельные тепловые потери р_уд=2,75 Вт/кг. Суммарные потери в сердечнике Ρ=р_удm = 2,75·2,43=6,68 Вт.

Ответ: Р=6,68 Вт.

1.1.12. Решить задачу 1.1.11 при условии, что стальной сердечник изготовлен из сплошного стального бруска. Все остальные данные без изменения.

Решение. Количество теплоты, выделяющееся в сердечнике, определим по формуле (1.7), где F=4·35·10^-3l_ср=4·35·280·10^-6=0,0392 м² - площадь охлаждающей поверхности магнитопровода. Тогда потери

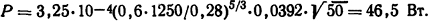
1.1.13. Определить количество теплоты, выделяемое в магнитопроводе электромагнита, катушка которого намотана круглым медным проводом диаметром d = 4 мм и имеет 250 витков. Магнитопровод изготовлен из листовой трансформаторной стали марки 1512, толщина листов δ=0,5 мм. Коэффициент заполнения магнитопровода k_з=0,9. При подключении катушки к источнику переменного напряжения частоты f = 50 Гц плотность тока составляет f = 1,0 А/мм². Эскиз магнитопровода приведен на рис. 1.2, где а = b = 70 мм, H = 320 мм, В =180 мм.

1.1.14. Решить задачу 1.1.13 при условии, что сердечник изготовлен из сплошного бруска стали, а остальные данные задачи 1.1.13 остались без изменения. Определить, во сколько раз потери в сплошном сердечнике больше потерь в шихтованном сердечнике при всех прочих равных условиях.

1.1.15. Определить длительно допустимую величину плотности переменного тока для бескаркасной цилиндрической катушки индуктивности, намотанной медным круглым проводом диаметром d=4 мм. Изоляция провода хлопчатобумажная без пропитки, число витков катушки N=250, высота катушки H=170 мм, а ее внутренний и наружный диаметры соответственно равны D_вн=100 мм, D_нap=155 м. Катушка находится в спокойном воздухе при температуре ϑ=35°C.

Решение. Согласно закону Джоуля - Ленца, потери энергии, выделяющиеся в катушке.

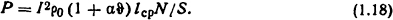
В длительном режиме работы вся выделенная в катушке энергия должна быть отведена в окружающую среду. Мощность, отводимая в окружающую среду, определяется по формуле (1.12) P=k_тF( ϑ- ϑ₀), где ϑ₀=35°С- температура окружающей среды; в качестве ϑ берем величину допустимой температуры для данного класса изоляции ϑ_доп = 90°С.

Коэффициент теплоотдачи определим из формулы (1.17).

Так как должно быть равенство между выделенной в катушке и отводимой с ее поверхности тепловыми мощностями, то исходным уравнением для нахождения допустимой плотности тока будет

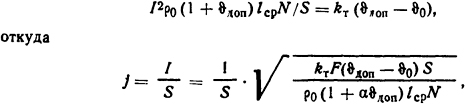
где S = πd²/4 = 3,14·4²·10^-6/4=12,56·10^-6 м² -площадь поперечного сечения провода; ρ₀=1,62·10^-8 Ом·м; α = 0,0043 К^-1; F=3,14(155+100)· 170·10^-6 + 2·3,14(155²-100²)10^-6/4 = 0,158 м²; l_ср=π(D_нар + D_вн)/2=3,14(0,155 + 0,1)/2 = 0,40 м - длина среднего витка катушки. Тогда по (1.17)

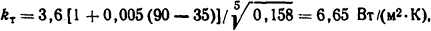
а плотность переменного тока

Ответ: j= 1,43 А/мм².

1.1.16. Определить допустимый ток для стальной трубы, имеющей наружный d_нар=26,8 мм и внутренний d_вн=3/4 дюйма диаметры, если по этой трубе протекает ток частоты f=50 Гц. Допустимая температура поверхности трубы ϑ_доп=95°С, а температура окружающей среды, которой является спокойный воздух, ϑ₀=35°С.

1.1.17. Определить длительно допустимое значение плотности переменного тока для цилиндрической катушки индуктивности, которая намотана проводом d=2 мм, имеет число витков N=500, наружный диаметр D_нар=136 мм, внутренний D_вн=70 мм, а ее высота h=72 мм.

1.1.18. Определить допустимое значение переменного тока круглой медной шины диаметром d=40 мм, установленной горизонтально в спокойном воздухе, температура которого ϑ₀=35°С, если частота тока f=50 Гц, а допустимая температура поверхности шины ϑ_доп=85°С.

1.1.19. Определить допустимый ток для медной трубы с внутренним d_вн=40 мм и внешним ϑ_нар=45 мм диаметрами, расположенной горизонтально в спокойном воздухе, температура которого ϑ₀=35°С. Частота переменного тока f=50 Гц, допустимая температура внешней поверхности трубы ϑ_доп=85°С.

1.1.20. Определить допустимый ток для медной шины, поперечное сечение которой 120×10 мм. Шина установлена на ребро в спокойном воздухе горизонтально. Частота переменного тока f=50 Гц, допустимая температура шины ϑ_доп=85°С, температура окружающей среды ϑ₀=35°С. Полученный результат сравнить с результатом, который получился бы для круглой шины при условии, что площадь ее поперечного сечения равна площади поперечного сечения прямоугольной шины.

1.1.21. Определить температуру медного круглого окрашенного краской проводника диаметром d=25 мм, по которому протекает постоянный ток I=1000 А. Проводник находится в спокойном воздухе с температурой ϑ₀=35°С.

Решение. Исходным уравнением для решения задачи должно быть равенство теплоты, выделяемой в проводнике и отдаваемой в окружающую среду с его боковой поверхности:

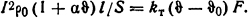
Коэффициент теплоотдачи из формулы (1.14)

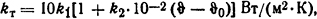
где k₁=1,17 Вт/(м²·К); k₂=1,0 К^-1.

Подставляя числовые значения в исходное уравнение и произведя расчеты на длине шины в один метр, получим

Решая последнее квадратное уравнение, находим ϑ=70°С.

Ответ: ϑ = 70°С.

1.1.22. Определить коэффициент теплоотдачи с поверхности шины, если длительно допустимая нагрузка для стальных шин прямоугольного сечения 100×4 мм (установленных на ребро) при протекании по ним постоянного тока не должна превышать 535 А. Максимальная температура шины ϑ = 80°С при температуре окружающего спокойного воздуха ϑ₀=35°С.

1.1.23. Определить температуру поверхности цилиндрической катушки без магнитопровода, через которую протекает постоянный ток I=20 А. Катушка с внутренним D_вн=100 мм и наружным D_нар=160 мм диаметрами, высотой h=170 мм, числом витков N = 250 расположена в спокойном воздухе, температура которого ϑ₀=35°С. Диаметр провода d = 4 мм.

1.1.24. Определить температуру поверхности прямоугольной алюминиевой шины размером 120×10 мм, если ее поверхность окрашена краской и по ней протекает постоянный ток I=2300 А. Шина установлена горизонтально на ребро в спокойном воздухе, температура которого ϑ₀ = 35°С.

1.1.25. Определить температуру круглого медного проводника, окрашенного краской, расположенного в спокойном воздухе,

температура которого ϑ₀=35°C; по проводнику диаметром d =45 мм протекает постоянный ток I=2500 А.

1.1.26. Определить температуру поверхности стальной трубы, по которой протекает переменный ток I=450 А частоты f=50 Гц. Труба окрашена масляной краской (внутренний диаметр d_вн = 3 дюйма, наружный d_нар=88,5 мм), расположена горизонтально в спокойном воздухе, температура которого ϑ₀=35°С.

1.1.27. Определить количество теплоты, выделяющееся в чугунном кольце высотой h=200 мм, с внутренним диаметром d = 100 мм и толщиной стенки δ = 50 мм, для случая, когда сквозь кольцо проходит шина с переменным током I=2000 А. Вычислить также температуру поверхности кольца, если частота переменного тока f=50 Гц, коэффициент теплоотдачи k_т = 17 Вт/(м²·К), а температура окружающей среды ϑ₀=35°C.

1.2. Неустановившиеся и квазистационарные процессы нагрева и охлаждения частей электрических аппаратов

В данном параграфе приведены задачи на вычисление постоянных времени нагрева и охлаждения электрических аппаратов, написание уравнений кривых нагрева, на расчет повторно-кратковременного режима нагрева и наиболее важного режима короткого замыкания (к.з.) с использованием кривых адиабатического нагрева и понятия фиктивного времени к.з. При этом используются следующие расчетные формулы и соотношения.

Зависимость температуры токоведущей части электрического аппарата от времени в процессе нагрева (кривая нагрева)

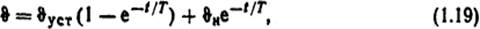
где ϑ_уст, ϑ_н - установившееся и начальное значения температуры, °С.

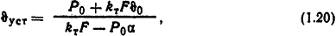
где Р₀ - мощность источников теплоты при 0°С, Вт; k_т - коэффициент теплоотдачи, Вт/(м²·К); F - охлаждающая поверхность, м²; ϑ₀ - температура окружающей среды, °С; α - температурный коэффициент сопротивления, 1/К; T - постоянная времени нагрева, с.

где С - теплоемкость электрического аппарата или его части, Дж/К.

В случае, когда k_тF≫P₀α,

где Р- мощность источников теплоты, Вт, при ϑ= ϑ_уст.

Зависимость температуры электрического аппарата от времени в процессе остывания (кривая охлаждения)

где Θ= ϑ- ϑ₀, Θ_н= ϑ_н- ϑ₀; T - постоянная времени нагрева, определяемая по формуле (1.22).

Время адиабатического нагрева токоведущей части электрического

Коэффициент перегрузки по мощности при повторно-кратковременном процессе нагрева

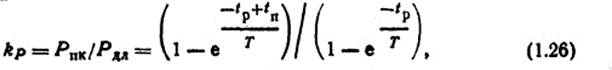
где Р_пк и P_дл - соответственно мощности источников теплоты при повторно-кратковременном и длительном процессах нагрева, Вт; t_р и t_п - соответственно время рабочего периода и паузы, с.

Коэффициент перегрузки по току при повторно-кратковременном процессе нагрева

Относительная продолжительность включения аппарата

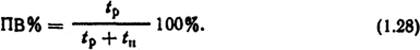
Фиктивное время короткого замыкания

где I_∞ - установившееся значение тока к.з., Α; i тока короткого замыкания, Α; *_к - действительное время, к.з., с.

Переходный процесс нагрева полубесконечного, стержня при наличии на его торце источника теплоты описывается выражением действительное значение

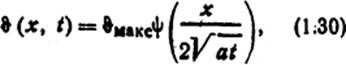
где х - координата точки на стержне, м, t - время, с, ϑ_макс - максимальное значение температуры (при x=0), °С, α - температуропроводность материала стержня, м²/с, , 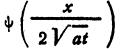- функция, график которой приведен на рис. 1.3.

Количество теплоты, передающееся в стержень за время t,

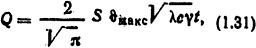
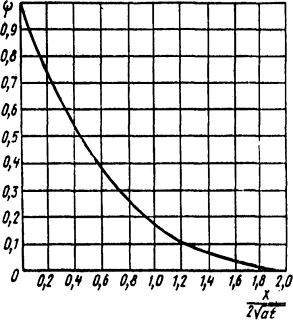
Рис. 1.3. График функции

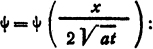
a - температуропроводность материала стержня, м²/с; x - координата, м; t - время

где S - площадь поперечного сечения стержня, м¹; λ - коэффициент теплопроводности материала стержня, Вт/(м·К), с -удельная теплоемкость материала стержня, Дж/(кг·К), γ - плотность материала стержня, кг/м³.

1.2.1. Написать уравнение кривой нагрева круглого медного проводника диаметром d=10 мм, по которому протекает постоянный

ток I=400 А. Известно, что коэффициент теплоотдачи < поверхности проводника k_т = 10 Вт/(м²·К), температура окружающей среды, которой является спокойный воздух, ϑ₀=35°С а значение удельного сопротивления меди за время нарастания температуры ρ=1,75·10^-8 Ом·м.

Решение. Уравнение кривой нагрева в простейшем случае при ϑ_н= ϑ₀ получаем из формулы (1.19)

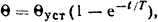
где Θ_уст = P/(k_тF) - установившееся превышение температуры. Расчет Θ_уст и Т произведем на единице длины проводника l=1 м по формулам (1.23 и (1.22) соответственно, т.е.

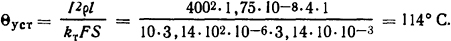
Постоянная времени нагрева