Простейшие методы расчета нагрева я охлаждения электрических аппаратов и их частей 4 страница

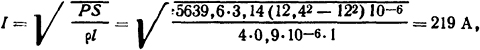
где S = 3,14(12,4²-12²)10^-6/4 м².

Ответ: I = 219 А.

1.4.16. Определить длительно допустимый переменный ток частоты f = 50 Гц для медной окисленной шины, расположенной горизонтально на ребро в спокойном воздухе. Размеры поперечного сечения шины 60×6 мм, допустимая температура для этой шины ϑ_доп=80°С, а температура окружающей среды ϑ₀=35°С.

1.4.17. Определить длительно допустимый ток для условий задачи 1.4.16, считая, что шина окрашена масляной краской.

1.4.18. Определить силу тока электрического нагревателя, предназначенного для обогрева комнаты, в которой температура воздуха ϑ₀=10°С. Нагреватель изготовлен из нихромовой проволоки диаметром d=1 мм, допустимая температура его ϑ_доп = 1000°С. Конструкция нагревателя такова, что для его расчета можно воспользоваться критериальным уравнением одиночного цилиндра. Расчет произвести с учетом теплоотдачи конвекцией н излучением. Степень черноты излучения нихрома ε = 0,75.

1.4.19. Определить температуру наружной поверхности цилиндрической катушки индуктивности, имеющей 500 витков, намотанной круглым медным проводом, диаметр которого d=2 мм. Провод катушки имеет бумажную изоляцию. Внутренний диаметр катушки D_вн=70 мм, наружный D_нар=140 мм, высота h=70 мм. По ней протекает ток I=5 А. Теплоотдача происходит только с наружной боковой поверхности, а торцы и внутренняя поверхность теплоизолированы. Катушка достаточно удалена от других тел и находится в спокойном воздухе, температура которого ϑ₀ = 35°С.

Решение. Будем считать, что средняя температура провода катушки равна температуре поверхности катушки. Тогда последняя определится из равенства

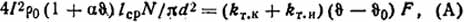
Поскольку коэффициенты теплоотдачи k_т.к и k_т.и нелинейно зависят от температуры, задачу будем решать методом подбора. Зададимся некоторой

температурой поверхности катушки, например ϑ₁ = 95°C, и определим ток в катушке, при которой ее поверхность будет иметь эту температуру. В качестве определяющего размера возьмем высоту катушки L = h = 70 мм. Для определяющей температуры ϑ_m = (95+35)/2=65°С из табл. П.9 находим: Pr_m=0,695; ν_m = 19,5·10^-6 м²/с; λ_m = 2,93·10^-2 Вт/(м·К); β_m = 1/338 К^-1. Тогда, используя формулу (1.34), получим

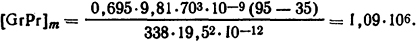
Коэффициент теплоотдачи конвекцией в соответствии с (1.33) и (1.38), поскольку Pr_m ≈ Рr_с, для воздуха будет равен

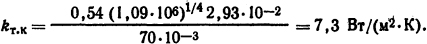
Коэффициент теплоотдачи излучением определим по формуле (1.52)

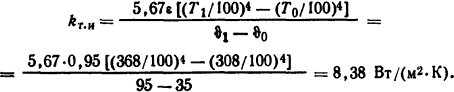
Для бумаги ε=0,95 (см. табл. П.12). Общий коэффициент теплоотдачи k_т = 7,3+8,38 = 15,68 Вт/(м²·К).

Из уравнения (А) и при ϑ₁= 95°С после некоторых вычислений

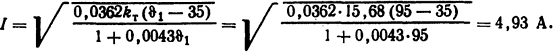
В условии задачи был задан ток I=5 А, Полученная Δ=(5-4,93)·100%/5=1,4% вполне достаточна. Если бы было получено значительное расхождение, то пришлось бы задаться новыми значениями ϑ₂, ϑ₃ и т.д. дс получения удовлетворительного совпадения.

Ответ: ϑ=95°С.

1.4.20. Рассчитать температуру поверхности круглой медной шины диаметром d=20 мм, обдуваемой поперечным потоком воздуха, скорость которого w = 0,5 м/с. Температура воздуха ϑ₀ =35°С. Шина окислена и по ней протекает переменный ток I = 1100 А частоты f=50 Гц.

1.5. Расчет распространения теплоты путем теплопроводности в частях электрических аппаратов

В данном параграфе рассмотрены задачи стационарного и переходной режимов теплопроводности для случаев одномерных тепловых потоков. За дачи на стационарную теплопередачу составлены с учетом использование понятия теплового сопротивления, что существенно облегчает их решение Приведены задачи для частей аппаратов как с внутренними источниками теплоты, так и без них.

В твердых частях электрических аппаратов теплота распространяете; теплопроводностью, причем разнообразие конструктивных форм частей, по которым распространяется теплота, накладывает определенные трудности на расчет этих частей.

При решении задач используются следующие расчетные формулы и соотношения.

Закон Ома для теплопроводности

где ( ϑ₁- ϑ₂) - перепад температур, К; Ρ - тепловой поток, Вт; R_т - тепловое сопротивление, К/Вт (см. табл. П. 13).

Координата наиболее нагретого слоя в плоской стенке с внутренними равномерно распределенными источниками теплоты и двусторонней изоляцией (рис. 1.9) (формула А.Г. Сливинской)

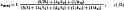
где δ и λ - толщина, м, и теплопроводность стенки, Вт/(м·К), с источниками теплоты; Δ₁ и λ₁ - толщина, м, и теплопроводность, Вт/(м·К), левой изоляционной стенки без источников теплоты; Δ₂ и λ₂ - толщина, м, и теплопроводность, Вт/(м·К), правой изоляционной стенки без источников теплоты; k_т1 и k_т2 - коэффициенты теплоотдачи, Вт/(м²·К), с левой и правой изоляционных стенок в окружающую среду.

Рис. 1.9. Плоская стенка с равномерно распределенными источниками теплоты

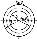
Рис. 1.10. Цилиндрическая стенка с равномерно распределенными источниками теплоты

Для цилиндрической стенки с равномерно распределенными источниками теплоты (рис. 1.10) радиус наиболее нагретого слоя

где k_т1 и k_т2 - коэффициенты теплоотдачи, Вт/(м²·К), с внутренней и наружной поверхностей цилиндрической стенки в окружающую среду, а λ - коэффициент теплопроводности стенки.

Объемная плотность источников теплоты в катушке

где IN - магнитодвижущая сила, А; ρ - удельное сопротивление материала проводника катушки, Ом·м; S_ок - площадь обмоточного окна, м²; k_з -коэффициент заполнения обмоточного окна (см. табл. П.24).

Диаметр проводника катушки постоянного тока

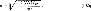
где l_ср - длина среднего витка катушки, м; U - напряжение, на которое включена катушка, В.

Приведенный к внутренней поверхности катушки коэффициент теплоотдачи для катушки постоянного тока с ферромагнитным сердечником при условии плотного прилегания катушки к сердечнику [1]

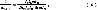
где k_т - коэффициент теплоотдачи с наружной поверхности магнитопровода, Вт/(м²·К); f_м- охлаждающая поверхность единицы длины наружной части магнитопровода, м²; S_m, λ_m - площадь поперечного сечения магнитопровода, м², и теплопроводность, Вт/(м·К), соответственно материала наружной части магнитопровода; 2l_м - длина наружной части магнитопровода, м; f_к - охлаждающая поверхность единицы длины внутренней части катушки, м²; l_к - длина катушки, м;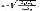

Приведенный к внутренней поверхности коэффициент теплоотдачи для катушки постоянного тока в случае наличия слоя изоляции и воздушного промежутка между магнитопроводом и катушкой

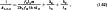
где δ_в, λ_в - толщина, м, и теплопроводность, Вт/(м·К), воздушного промежутка; λ_и, λ_н - то же, для слоя изоляции.

Теплопроводность замещающего тела для [1] непропитанных катушек, намотанных круглым медным проводом при рядовой намотке,

где λ_и и λ_Β - соответственно теплопроводность изоляции обмоточного провода и воздуха, Вт/(м·К); d - диаметр голого провода, м; δ - толщина изоляции на проводе, м.

Коэффициент теплопроводности замещающего тела для пропитанных катушек [1] при рядовой намотке

где λ_и.л - средняя теплопроводность изоляции проводника и пропиточного лака, Вт/(м·К).

Теплопроводность замещающего тела непропитанных катушек, намотанных круглым медным проводом при шахматной намотке,

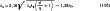
где обозначения те же, что и в (1.63).

Теплопроводность замещающего тела пропитанных катушек, намотанных круглым медным проводом при шахматной намотке,

где обозначения те же, что и в (1.64).

Распределение температуры вдоль бесконечно длинного стержня, в торец которого входит тепловой поток Ρ (Вт), а с наружной поверхности

теплоотдача происходит в окружающую среду с коэффициентом теплоотдачи k_т, Вт/(м²·К) [2],

где ϑ - температура поверхности стержня, °С; ϑ_макс - максимальная температура в торце стержня, °С,

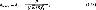
S - площадь поперечного сечения стержня, м²; f_c - периметр поперечного сечения длины стержня, м:

x - координата длины, м, k_т - коэффициент теплоотдачи с поверхности стержня, Вт/(м²·К); λ - теплопроводность материала стержня, Вт/(м·К).

Длина стержня, с которой отводится в окружающую среду тепловой поток ΔΡ,

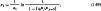
где Р_x=0 - тепловой поток, проходящий через сечение х=0, Вт.

Тепловой поток, который отводится с поверхности стержня длиной l в окружающую среду,

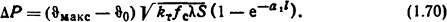
Распределение температуры вдоль стержня ограниченной длины [2]

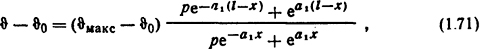
где ϑ_макс - максимальная температура стержня при x=0, °С,

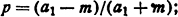
l - длина стержня, м, m=k_т/λ.

Суммарный тепловой поток, который отдается в окружающую среду со всей поверхности стержня (тепловой поток, проходящий через поперечное сечение стержня при х=0),

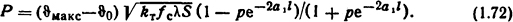
Для полуограниченного стержня неизменного сечения с равномерно распределенными источниками теплоты в нем при наличии внешнего источника теплоты на его торце зависимость температуры стержня от его длины [2]

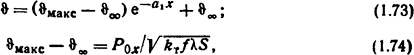
где ϑ_макс - максимальная температура стержня, °С; Р_0х - тепловой поток, входящий в торец стержня, Вт;

ϑ_∞ - температура поверхности стержня на удалении от торца, °С. q - объемная плотность источников теплоты, Вт/м³.

Распределение температур в стержне, имеющем ступенчато-изменяющееся сечение при условии наличия внутренних источников теплоты (рис. 1.11) [2]:

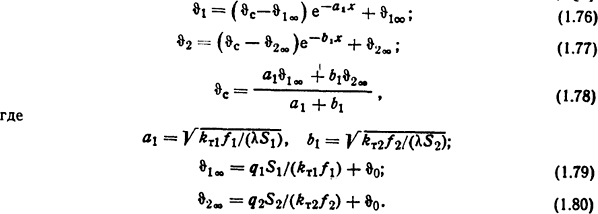
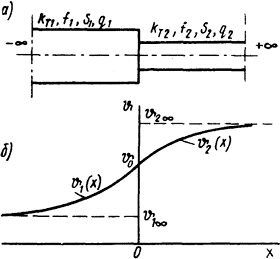
Рис. 1.11. Стержень с внутренними источниками теплоты со ступенчато изменяющимся поперечным сечением (а) и распределение температуры вдоль его длины (б)

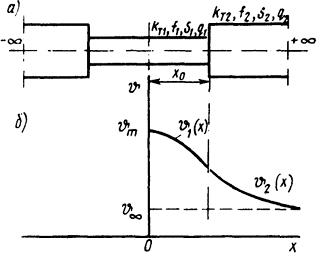
Рис. 1.12. Стержень с внутренними источниками теплоты с утоньшением (а) и распределение температуры вдоль его длины (б)

Распределение температур в стержне с внутренними источниками теплоты при наличии участка уменьшенного сечения в средней части стержня в установившемся режиме нагрева [2] (рис. 1.12):

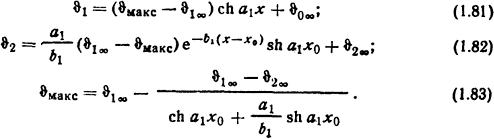
Значения параметров а₁ и b₁, а также температур ϑ_1∞ и ϑ_2∞ те же, что и в формулах (1.76), (1.77) и (1.78). Распределение температур в стержне с равномерно распределенными источниками теплоты при наличии участка увеличенного сечения [2] (рис. 1.13):

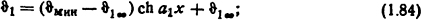
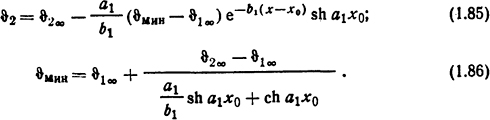
Значения параметров a₁, b₁ и температур ϑ_1∞ и ϑ_2∞ те же, что и в формулах (1.76), (1.77) и (1.78).

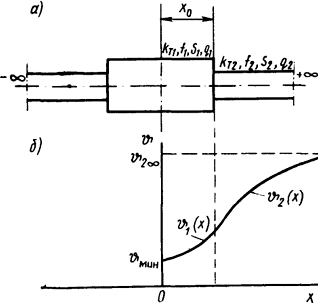
Рис. 1.13. Стержень с внутренними источниками теплоты с утолщением (а) и распределение температуры вдоль его длины (б)

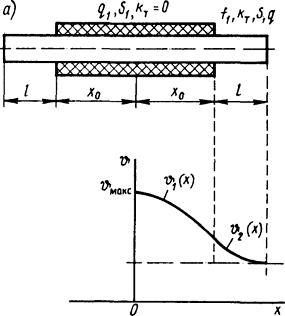
Рис. 1.14. Стержень с внутренними источниками теплоты с тепловой изоляцией в средней части его (а) и распределение температур вдоль его длины (б)

Распределения температур в однородном конечной длины стержне с равномерным распределением источников теплоты, в средней части покрытого слоем теплоизоляции с граничными условиями [2] (рис. 1.14):

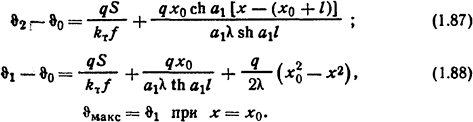
1.5.1. Определить количество теплоты, передаваемое через 1 м² текстолитовой плоской стенки толщиной δ =20 мм. Разность температур на поверхностях стенки Δ ϑ=30°0.

Решение. Воспользуемся аналогом закона Ома для теплопроводности [см. формулу (1.56)]:

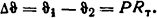
Тепловое сопротивление плоской стенки без источников теплоты (см. табл. П.13):

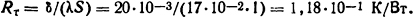
Теплопроводность λ определим из табл. П. 14.

Тогда тепловой поток

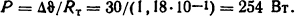
Ответ: P = 254 Вт.

1.5.2. Определить перепады температур в слоях плоской стенки площадью S=2 м², которая выполнена из углеродистой стали толщиной δ₁=2 мм и пенопласта толщиной δ₂=10 мм, если количество теплоты, проходящее через стенку за 1 ч, составляет 1,9 кВт·ч. Теплопроводность стали λ₁ = 54 Вт/(м·К), пенопласта λ₂=0,1 Вт/(м·К).

1.5.3. Определить перепад температур в слое изоляции прямоугольной медной шины размером 100×10мм, покрытой слоем бумажной изоляции толщиной δ=2 мм. В результате протекания по шине тока в каждом ее метре выделяется теплота Ρ=60 Вт/м, которая отводится через слой изоляции к окружающему воздуху.

1.5.4. Рассчитать перепад температур в толще изоляции для условий задачи 1.5.3, если шина кроме бумажной изоляции покрыта еще слоем лакоткани толщиной δ = 1 мм. Теплопроводность лакоткани λ=0,15 Вт/(м·К).

1.5.5. Определить максимальный ток для круглой алюминиевой шины диаметром d = 38 мм. Шина находится в трубе диаметром d_тp = 40 мм, температура поверхности шины ϑ_ш=50°С, внутренней поверхности трубы ϑ_тр=35°C. Между шиной и трубой, которые расположены концентрично, находится спокойный сухой воздух.

1.5.6. Определить тепловое сопротивление и тепловой поток через чугунную стенку толщиной δ=10 мм, которая является стенкой масляного бака и имеет площадь S=2 м², если известно, что температура масла в баке равна 85°С, а температура наружной поверхности бака - 45°С. Теплопроводность чугуна λ = 47 Вт/(м·К) при 0°С, температурный коэффициент теплопроводности β = - 4·10^-4 К^-1.

1.5.7. Вычислить температуру поверхности токоведущего медного стержня диаметром d = 38 мм, заключенного внутри металлической трубы с внутренним диаметром d_вн=40 мм. По стержню протекает постоянный ток I = 1800 А, температура внутренней поверхности трубы ϑ_вн=30°С, между стержнем и трубой находится сухой воздух. Считать, что передача теплоты от поверхности стержня осуществляется только теплопроводностью. Учесть зависимость теплопроводности воздуха от температуры.

Решение. Для решения задачи воспользуемся законом Ома для теплопроводности по формуле (1.56) ϑ_ст- ϑ_тр=PR_т. Здесь Ρ=I²ρ₀(1+α ϑ_ст)l/S -

тепловой поток, выделяемый в стержне и проходящий через воздушную прослойку в единицу времени, т.е. тепловая мощность;

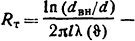
тепловое сопротивление цилиндрической воздушной прослойки: ρ₀=1,62·10⁸ Ом·м; α = 0,0043.

Окончательно исходное уравнение получаем в виде

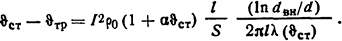
Решим данное уравнение относительно тока I и подставим в него числовые значения. После преобразования получим

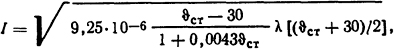
где λ[( ϑ_ст+30)/2]-зависимость теплопроводности от средней температуры воздуха _ст= (Ф_ст+30)/2.

Зададимся несколькими значениями ϑ_ст:

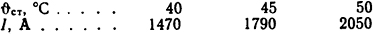
и по этим данным построим график I=I( ϑ_ст) (рис. 1.15), по которому для I=1800 А определяем ϑ_ст=45,2°С.

Ответ: ϑ_ст=45,2°С.

1.5.8. Определить температуру прямоугольной алюминиевой шины с размерами поперечного сечения 100×10 мм, покрытой слоем бумажной изоляции толщиной δ= 3 мм, если известно, что по шине протекает постоянный ток I =2000 А. Температура наружной поверхности изоляции ϑ_из = 40°С.

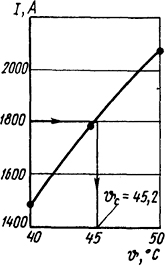
Рис. 1.15. Построение графика к задаче 1.5.7 и определение температуры стержня

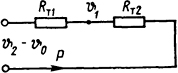
Рис. 1.16. Схема замещения

1.5.9. Определить перепад температур в толще изоляции Δ ϑ и температуру медного бесконечно длинного стержня диаметром d = 20 мм, покрытого слоем бакелизированной бумаги толщиной δ = 5,0 мм, если по нему протекает переменный ток I = 600 А частоты f = 50 Гц. Стержень находится в спокойном воздухе, температура которого ϑ₀ = 35°C. Теплопроводность бакелизированной бумаги λ = 0,2 Вт/(м·град).

Решение. Составим электрическую схему замещения (рис. 1.16) и запишем уравнение, аналогичное закону Ома для электрической цепи:

Тепловой поток, выделяющийся в стержне, определим из формулы (1.2); при k_б=1 Ρ=k_пI²ρ₀(1+α ϑ₂)/S. Он равен тепловому потоку через толщу изоляции на единице длины стержня; R_т1 = 1/k_тF - тепловое сопротивление потоку Ρ от наружной поверхности изоляции воздуху;

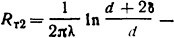
тепловое сопротивление толщи изоляции; ϑ₂ - температура стержня; k_п - коэффициент поверхностного эффекта, зависящий от - площадь поперечного сечения стержня; k_т=12[1 + 10^-2( ϑ₁ - ϑ₀)], Вт/(м²·К)- коэффициент теплоотдачи от наружной поверхности к спокойному воздуху [см. формулу (1.14) и табл. 1.1]; F=π(d+2δ) - боковая поверхность единицы длины изолированного стержня; ϑ₁ - температура наружной поверхности изоляции.

Для условий данной задачи k_п≈1; ρ₀= 1,62·10^-8 Ом·м; α =0,0043 К^-1.

Таким образом, закон Ома запишется в виде

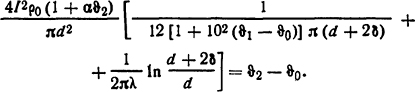
Для нахождения ϑ₂ и ϑ1 составим еще одно уравнение, исходя из схемы замещения, а именно: РR_т2= ϑ₂- ϑ₁, тогда

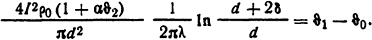
После подстановки и преобразований получим систему уравнений

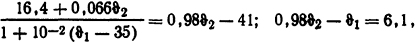
решая которую найдем: ϑ₂=60°С; ϑ₁=52,8°С; Δ ϑ= ϑ₂- ϑ₁=7,2°C.

Ответ: Δ ϑ=7,2°C; d₂=60°C.

1.5.10. Определить температуру наружной поверхности изоляции круглого медного проводника диаметром d=40 мм, по которому протекает ток I=2250 А, в результате чего поверхность оказывается нагретой до температуры ϑ=60°С. Проводник покрыт двумя изоляционными слоями: слоем бумаги с теплопроводностью λ₁=0,1 Вт/(м·К) и слоем лакоткани с теплопроводностью λ₂=0,2 Вт/(м·К). Толщина бумажной изоляции δ₁=4 мм; толщина изоляции из лакоткани δ₂=6 мм.

1.5.11. Вычислить допустимую силу тока алюминиевого проводника круглого поперечного сечения диаметром d=40 мм, покрытого двумя слоями изоляции: слоем бумаги, толщина которого δ₁ =4 мм, и слоем лакоткани, толщина ксторого δ₂=6 мм. Допустимая температура наружной поверхности изоляции ϑ₂ =70°С, внутренней поверхности ϑ₁=80°C. Теплопроводность для бумаги λ₁=0,1 Вт/(м·К), для лакоткани λ₂=0,2 Вт/(м·К).

1.5.12. Определить критический диаметр изоляции и допустимую силу тока для круглой медной шины диаметром d=22 мм, которая изолирована слоем стеклоткани, изготовленной на кремнийорганике.

Максимально допустимая температура изоляции ϑ_доп=180°С. Шина находится в спокойном воздухе, температура которого ϑ₀=35°C, коэффициент теплоотдачи от наружной поверхности стеклоткани к окружающей среде k_т=10 Вт/(м²·К). Теплопроводность изоляции λ_из=0,25 Вт/(м·К).

1.5.13. Определить допустимую плотность тока медного круглого проводника диаметром d=2 мм, если толщина резиновой изоляции на нем такова, что наружный ее диаметр равен критическому. Допустимая температура для резиновой- изоляции ϑ_доп=60°С, теплопроводность λ=0,16 Вт/(м·К); проводник находится в спокойном воздухе, температура которого ϑ₀=35°С, коэффициент теплоотдачи от наружной поверхности изоляции воздуху k_т=0,9 Вт/(м²·К).

1.5.14. Определить полное тепловое сопротивление алюминиевой шины, поперечное сечение которой 120×10 мм. Шина расположена горизонтально в спокойном воздухе. В результате протекания по ней тока она нагрелась до температуры ϑ=90°C.

Тепловое сопротивление шины определять как тепловое сопротивление плоской стенки с равномерно распределенными в ней источниками теплоты. Учесть зависимость теплопроводности от температуры и предположить, что теплота равномерно отводится от широких сторон, шины, а шина находится в спокойном воздухе с температурой ϑ₀ = 35°С. Коэффициент теплоотдачи с поверхности шины k_т = 5 Вт/(м²·К).

1.5.15. Вычислить наибольшую температуру в стальной шине размером 100×10 мм, по которой протекает постоянный ток I=1000 А, шина расположена в спокойном воздухе таким образом, что теплоотдача с ее поверхности в окружающее пространство происходит с одной широкой ее плоскости. Коэффициент теплоотдачи с поверхности шины окружающему воздуху k_т=10 Вт/(м²·К), а температура окружающего воздуха ϑ₀=35°С. Удельное сопротивление стали ρ=13·10^-8 Ом·м и теплопроводность λ =40 Вт/(м·К) принять не зависящими от температуры.

Решение. Воспользуемся выражением закона Ома для теплопроводности типа (1.56)

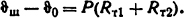
Мощность, выделяемую в единице длины шины, определим из (1.2). Так как k_п=k₆=1, то

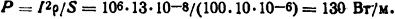
Тепловые сопротивления в соответствии с табл. П.13.

Здесь F=S=100·1·10^-3 м².

Тогда ϑ_ш=130 (0,00125+1) +35 =165°С.

Ответ: ϑ_ш=165°С.

1.5.16. Решить задачу 1.5.15 при условии, что теплоотдача происходит равномерно с двух сторон полосы, а остальные данные остались без изменения.

1.5.17. Определить наибольшую температуру в шине, попе речные размеры которой 100×10 мм, обтекаемой потоком сухого воздуха с такой скоростью, что коэффициент теплоотдачи с боковых широких ее сторон k_т = 25 Вт/(м²·К). По шине протекает постоянный ток I=4000 А. Удельное сопротивление материала шины ρ = 2,2·10^-3 Ом·м, теплопроводность λ = 400 Вт/(м·К), температура воздуха ϑ₀ = 20°C.

1.5.18. Определить наибольшую температуру и температуру наружной поверхности трубы, по которой протекает переменный ток I=450 А частоты f=50 Гц. Вся теплота, выделяющаяся в трубе, отдается с ее наружной поверхности спокойному окружающему воздуху. Коэффициент теплоотдачи с поверхности трубы k_т=25 Вт/(м²·К), температура воздуха ϑ₀=35°С, наружный диаметр трубы d_нар=88,5 мм, внутренний d_вн=3 дюйма.

Решение. Исходными уравнениями при решении задачи будут ϑ_макс - ϑ₀ = Ρ(R_т1+R_т2) и ϑ_макс - ϑ_нар = PR_т1. Тепловые сопротивления на длине l=1 м определим на основании табл. П. 13.

где r = 37 мм и R = 44,25 мм - соответственно внутренний и наружный радиусы трубы, а λ=40 Вт/(м·К) - теплопроводность стали.