Простейшие методы расчета нагрева я охлаждения электрических аппаратов и их частей 5 страница

Мощность Р, выделяемую в единице длины стальной трубы, определяем из формулы (1.6), приняв в качестве числового коэффициента максимальное значение

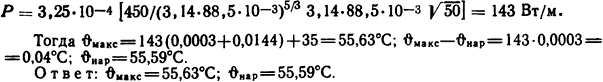
Тогда ϑ_макс=143(0,0003+0,0144)+35=55,63°С; ϑ_макс- ϑ_нар= 143·0,0003 = 0,04°С; ϑ_нар=55,59°С.

Ответ: ϑ_макс= 55,63°С; ϑ_нар=55,59°С.

1.5.19. Определить температуру оси круглой шины диаметром d=15 мм. По шине протекает ток I = 6000 А. Температура потока воды, который ее обтекает, ϑ₀=25°С. Коэффициент теплоотдачи с поверхности шины k_т = 1000 Вт/(м²·К). Удельное сопротивление материала шины ρ= 2,2·10^-8 Ом·м, теплопроводность λ =400 Вт/(м·К).

1.5.20. Найти температуру наиболее нагретого слоя, его координату и температуры поверхностей изоляции плоской алюминиевой шины размером 120×10 мм, по которой протекает постоянный ток I=2000 А. Шина с одной широкой стороны изолирована пластиной текстолита толщиной Δ₁= 10 мм, а другой стороной прилегает к стенке из асбоцемента, толщина которой Δ₂ = 20 мм. Шина находится в спокойном воздухе, температура которого

ϑ₀=35°С. Коэффициенты теплоотдачи с поверхности текстолита k_т1=20 Вт/(м²·К), а с поверхности асбоцемента k_т2 = 15 Вт/(м²·К). Удельное сопротивление алюминия принять независимым от температуры и равным ρ= 2,9·10^-8 Ом·м, его теплопроводность λ=210 Вт/(м·К), теплопроводность текстолита λ₁ = 0,15 Вт/(м·К), асбоцемента λ₂=0,6 Вт/(м·К).

Решение. Определим координату наиболее нагретого слоя в шине по формуле (1.57)

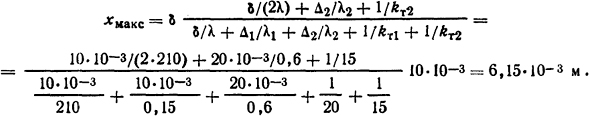
Объемная плотность источников теплоты, выделяющейся в шине,

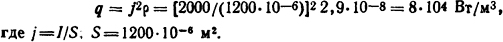
где j=I/S, S = 1200·10^-6 м².

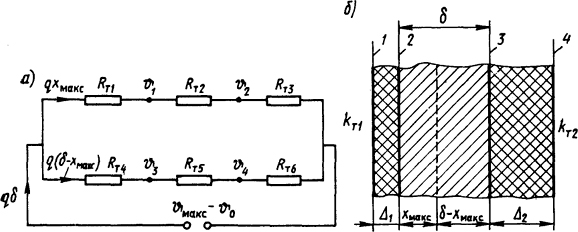
Рис. 1.17. Схема замещения (а) и эскиз плоской стенки с равномерно распределенными источниками теплоты (б)

Эквивалентная схема замещения представлена на рис. 1.17, а. Здесь ϑ₁, ϑ₂, ϑ₃ и ϑ₄ - температуры стенок 1, 2, 3 и 4 соответственно (рис. 1.17, б):

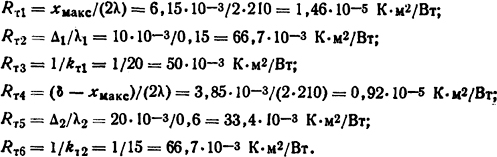
Из уравнения ϑ_макс - ϑ₀=qx_макс(R_т1 + R_т2 + R_т3)=8·10⁴·6,15·10^-3·(1,46·10^-5+66,7·10^-3+50·10^-3)=57°C температура наиболее нагретого слоя ϑ_макс = 92°C.

Исходя из закона Ома (1.56) и рис. 1.17, а, ϑ_макс- ϑ₀=qx_максR_т1 = 8·10⁴·6,15·10^-3·1,46·10^-5=0,0072°C, откуда ϑ₁ = 91,9928≈92°С = ϑ_макс.

Аналогично определяем: ϑ₂=59,5°С; ϑ₃≈ ϑ_макс = 92°С; ϑ₄ = 55,6°С.

Ответ: ϑ_макс=92°С; ϑ_макс = 6,15 мм; ϑ₁=92°С; ϑ₂=59,5°С; ϑ₃=55,6°С.

1.5.21. Найти координату наиболее нагретого слоя, значение наибольшей температуры и температуру на поверхностях стальной шины с поперечными размерами 100×10 мм, расположенной горизонтально в спокойном воздухе, температура которого ϑ₀ = 35°С. По шине протекает постоянный ток I=1000 А. Шина находится между двумя пластинами из изоляционного материала, которые изолируют ее широкие стороны. С одной стороны изоляционная пластина имеет толщину Δ₁ = 10 мм и изготовлена из фторопласта-4, с другой стороны имеет толщину Δ₂ = 20 мм и изготовлена из электрокартона. Коэффициент теплоотдачи с поверхностей фторопласта k_т1 = 8 Вт/(м²·К), электрокартона k_т2 = 15 Вт/(м²·К). Удельное сопротивление стали ρ=14·10⁸ Ом·м, теплопроводность стали λ=45 Вт/(м·К), фторопласта λ₁ ="0,3 Вт/(м·К), электрокартона λ₂=0,2 Вт/(м·К).

1.5.22. Определить температуры поверхностей стальной трубчатой шины, охлаждаемой с наружной стороны потоком воздуха, с внутренней - потоком воды. По шине протекает постоянный ток I=1250 А. Внутренний диаметр шины d_вн=3/8 дюйма, наружный d_нар=17 мм. Коэффициенты теплоотдачи воде k_т1 = 1000 Вт/(м²·К), воздуху k_т2=100 Вт/(м²·К), температура воды и воздуха ϑ₀₁ = ϑ₀₂ = ϑ = 20°C. Удельное сопротивление стали принять равным ρ=15·10⁸ Ом·м и не зависящим от температуры, теплопроводность λ = 45 Вт/(м·К).

Решение. Радиус наиболее нагретого слоя определим по формуле

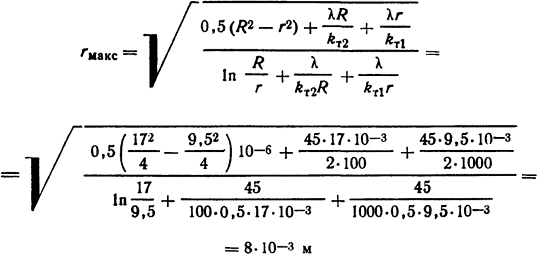
Объемная плотность источников теплоты в стенке трубы

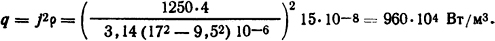
Весь расчет будем вести для длины трубы l=1 м. Тепловое сопротивление от наиболее нагретого слоя к наружной поверхности определим из табл. П.13:

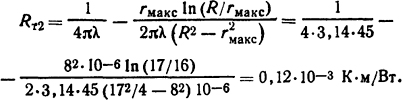
Тепловое сопротивление от наружной поверхности трубы к охлаждающему воздуху (см. табл. П.13)

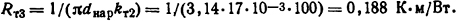
Из равенства, аналогичного формуле (1.56),

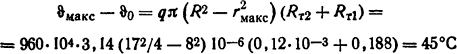
наибольшая температура ϑ_макс=65°C.

Температура наружной поверхности стенки трубы в соответствии с законом Ома вида (1.56)

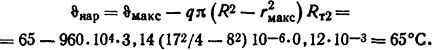
Температура внутренней поверхности трубы

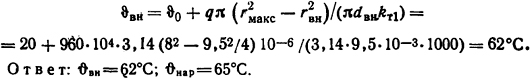
Ответ: ϑ_вн=62°C; ϑ_нap=65°C.

1.5.23. Определить температуры поверхностей медного токопровода, изготовленного в виде трубы с d_нар=40 мм, d_вн=36 мм, если известно, что по токопроводу протекает ток I=2500 А, а с внутренней и наружной поверхностей трубопровода коэффициенты теплоотдачи равны k_т=200 Вт/(м²·К) за счет масляного охлаждения. Температура масла ϑ₀=35°C.

1.5.24. Найти максимальную температуру, а также температуры поверхностей катушки постоянного тока, имеющей 1270 витков медного провода марки ПЭВТЛ, намотанных рядовой намоткой без пропитки. Размеры катушки даны на рис. 1.18. Диаметр провода d=0,35 мм, толщина

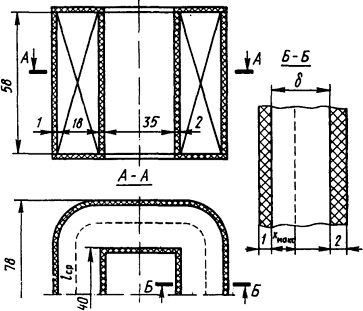
Рис. 1.18. Эскиз катушки

слоя изоляции на нем δ = 0,02 мм. По катушке протекает ток I=0,54 А. Катушка находится в спокойном воздухе, температура которого ϑ₀=35°C. Каркас изготовлен из текстолита, на наружной поверхности имеется слой лакоткани, коэффициент теплоотдачи с поверхности которой k_т1=8 Вт/(м²·К), с внутренней поверхности катушки k_т2=12 Вт/(м²·К). Удельное сопротивление меди принять независимым от температуры и равным ρ=2,0·10^-8 Ом·м, теплопроводность текстолита λ₁ = 0,15 Вт/(м·К), лакоткани λ₂ = 0,5 Вт/(м·К).

Решение. Решение задачи будем искать для сечения Б-Б. Объемная плотность источников теплоты в катушке определится из формулы

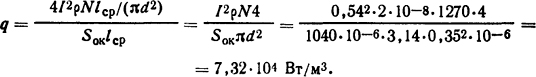
Здесь S_ок=1040·10^-6 м² - площадь обмоточного окна.

Теплопроводность замещающего тела для слоя катушки определим из формулы (1.63)

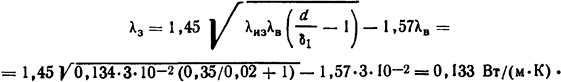
Здесь λ_из=0,134 Вт/(м·К) (см. табл. П.15); λ_в=3·10^-2 Вт/(м·К). Зная значения q и λ, можем решать задачу, применяя формулы для плоской стенки с равномерно распределенными источниками теплоты.

Координата наиболее нагретого места в катушке x_макс = 8,3 мм. Дальнейшее решение задачи совершенно аналогично решению задачи 1.5.20 с такой же эквивалентной схемой замещения. Следуя решению задачи 1.5.20, получим: ϑ_макс=138°С; ϑ_вн=110°С; ϑ_нар=94°С.

Ответ: ϑ_макс=138°С; ϑ_вн=110°С; ϑ_нар=94°С.

1.5.25. Решить задачу 1.5.24 при условии, что ток, протекающий через катушку, I=0,6 А, катушка пропитана изоляционным лаком с теплопроводностью λ_лак=0,116 Вт/(м·К). Определить перепад температур в слоях изоляционного каркаса и лакоткани и построить график изменения температуры по сечениям слоя катушки, изоляционного каркаса и лакоткани.

1.5.26. Рассчитать наибольшую температуру, радиус наиболее нагретого слоя и температуру внутренней и наружной поверхностей цилиндрической бескаркасной катушки постоянного тока, которая намотана круглым медным проводом диаметром d = 4 мм. Провод изолирован бумажной изоляцией толщиной δ = 0,5 мм. Катушка расположена в спокойном воздухе, температура которого ϑ₀ = 35°С. Коэффициенты теплоотдачи с внутренней и наружной поверхностей одинаковы: k_т = 7 Вт/(м²·К). Внутренний диаметр катушки D_вн=100 мм, наружный диаметр D_нар=156 мм, ее высота h=170 мм. По катушке протекает постоянный ток, плотность которого j=1,5 А/мм². Катушка намо-

рядовой намоткой и имеет 250 витков. Удельное сопротивление меди ρ = 2,3·10⁸ Ом·м принять независимым от температуры, теплопроводность бумажной изоляции λ_из=0,1 Вт/(м·К), воздуха λ_в=3·10^-2 Вт/(м·К).

1.5.27. Найти температуру наиболее нагретого слоя, а также температуры поверхностей катушки постоянного тока с шихтованным магнитопроводом (рис. 1.19, а). Число витков медного

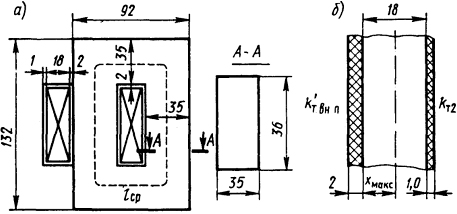
Рис. 1.19. Эскиз катушки на магнитопроводе (а) и разрез катушки (б)

провода марки ПЭВ равно 1250. Диаметр провода d=0,35 мм, толщина изоляции δ = 0,02 мм. Катушка пропитана изоляционным лаком λ_лак=0,095 Вт/(м·К). Между текстолитовым каркасом и магнитопроводом имеется воздушный промежуток толщиной δ_в=0,5 мм, с наружной поверхности катушка изолирована слоем лакоткани, теплопроводность которой λ₂=0,15 Вт/(м·К). По катушке протекает ток I=0,6 А, коэффициенты теплоотдачи с поверхностей магнитопровода k_т = 15 Вт/(м²·К), катушки k_т1 = 10 Вт/(м²·К), теплопроводность текстолита λ_из=0,5 Вт/(м·К), стали λ₂=46 Вт/(м·К), воздуха λ_в=0,03 Вт/м·К, а коэффициент заполнения стали k_з=0,9.

Решение. Находим коэффициент теплоотдачи, приведенный к внутренней поверхности катушки. Для этого воспользуемся формулой, которая учитывает слой изоляционного каркаса и слой воздуха, а именно формулой (1.62):

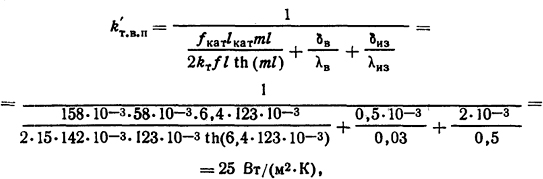
где f_кaт = 2(35+4) +2(36+4) = 158·10^-3 м; f = 2(35+36) = 142·10^-3 м; = 15 Вт/(м²·К);

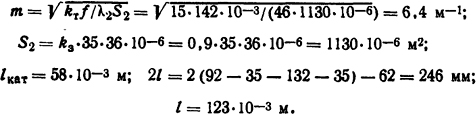
После определения приведенного к внутренней поверхности коэффициента теплоотдачи катушку с магнитопроводом можно заменить катушкой без магнитопровода, т.е. можно полагать, что внутренняя поверхность катушки охлаждается какой-то фиктивной средой с коэффициентом теплоотдачи k’_т.в.п и температурой ϑ₀=35°С.

Координата наиболее нагретого слоя (рис. 1.19, б) определится, как для плоской стенки [см. формулу (1.57)], с той лишь разницей, что вместо λ необходимо подставить из формулы (1.64) λ_з = λ_лак(d/δ)^2/3 = 0,095 [0,35·10^-3/(0,02·10^-3)]^2/3 =0,138 Вт/(м·К). После вычислений x_макс=12,1 мм.

Объемную плотность источников теплоты определим по формуле (1.59) q = (IN)²ρ/(S²_окk_з) = (0,6·1250)²·2,2·10^-8/[(18·58)²·10^-12·0,45] = 2,54·10⁴ Вт/м³, где ρ = 2,2·10^-8 Ом·м - удельное сопротивление для меди, соответствующее средней температуре провода ϑ≈80°С; k_з = 0,45 - коэффициент заполнения катушки, определенный по [1] для катушки, намотанной проводом d= 0,35 мм с автоматической подачей; S_ок = 18·58 мм² - площадь обмоточного окна. Тогда

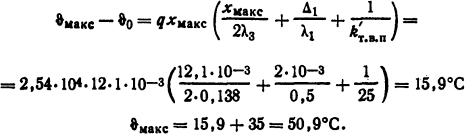
Аналогично определяем:

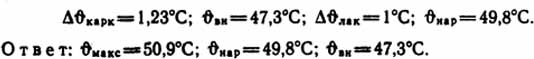
Ответ: ϑ_макс=50,9°C; ϑ_нар=49,8°С; ϑ_вн=47,3°С.

1.5.28. Определить радиус наиболее нагретого слоя, его температуру, а также температуру внутренней и наружной поверхностей цилиндрической катушки индуктивности, которая намотана круглым медным проводом диаметром d=2 мм непосредственно на цилиндрический магнитопровод. Катушка имеет 500 витков и по ней протекает постоянный ток I=4,5 А. Магнитопровод катушки замкнут, и его внешняя часть имеет прямоугольное сечение, площадь которого равна площади поперечного сечения круглой части магнитопровода (размеры магнитопровода показаны на рис. 1.20). Высота катушки h= 72 мм, наружный диаметр D_нар=136 мм, внутренний D_вн=70 мм. Изоляция провода бумажная, толщина которой δ₁ =0,25 мм. Катушка намотана рядовой намоткой и пропитана. Построить график изменения

температуры вдоль наружной части магнитопровода, если коэффициенты теплоотдачи с наружных частей магнитопровода k_т1=20 Вт/(м²·К), катушки k_т2= 10 Вт/(м²·К). Катушка намотана на магнитопровод достаточно плотно, находится в спокойном воздухе, температура которого ϑ₀=35°С. Удельное сопротивление меди принять независящим от температуры и равным ρ=2,2·10^-8 Ом·м, теплопроводность бумажной изоляции λ_из=0,122 Вт/(м·К), воздуха λ_в=0,03 Вт/(м·К), стали λ_ст=46 Вт/(м·К).

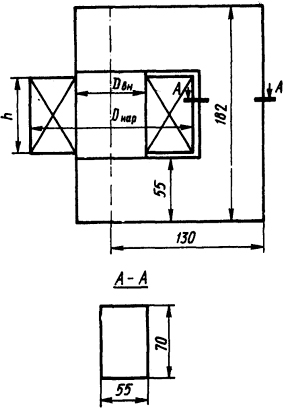
Рис. 1.20. Эскиз магнитопровода катушкой

1.5.29. Определить установившееся значение температуры медного круглого стержня диаметром d=10 мм на расстоянии 0,5 м от его торца, который находится в расплавленном олове, имеющем температуру ϑ_макс=250°С. Стержень находится в воздухе с ϑ₀=35°С, при этом коэффициент теплоотдачи с его поверхности k_т = 25 Вт/(м²·К). Определить также тепловой поток, который отводится с боковой поверхности стержня длиной 0,5 м, считая от поверхности олова.

Решение. Из формулы (1.73)

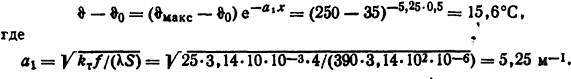
Здесь λ=390 Вт/(м·К) - теплопроводность меди (см. табл. П.7). Тогда температура стержня ϑ=50,6°С.

Значение теплового потока с боковой поверхности стержня [2]

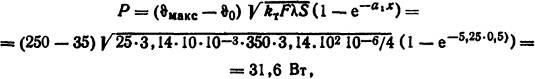
где F=3,14·10·10^-3 м², a S=3,14·10^-6/4 м².

Ответ: ϑ=50,6°С; Р=31,6 Вт

1.5.30. Определить, на каком расстоянии можно держать голой рукой медный круглый стержень диаметром d=20 мм, торец которого приставили к поверхности расплавленного олова с температурой

ϑ_макс = 300°С. Рука может выдержать длительную температуру ϑ_дл = 50°С. Температура окружающего воздуха ϑ₀= 20°С, средний коэффициент теплоотдачи с поверхности стержня окружающему воздуху k_т = 20 Вт/(м²·К). Средняя теплопроводность меди λ=350 Вт/(м·К).

1.5.31. Определить температуру электрода из нержавеющей стали непосредственно у держателя, который находится на рас стоянии l₁=250 мм от свариваемой поверхности, а также темпе ратуру электрода в конце сварки, когда его длина уменьшилась до l₂=50 мм. Электрод имеет прямоугольное сечение, размеры; которого 3×3 мм. Коэффициент теплоотдачи с поверхности электрода k_т = 25 Вт/(м²·К), теплопроводность нержавеющей стали λ=Вт/(м·К), температура торца электрода ϑ_макс = 15000°С температура воздуха ϑ₀=20°С. При расчете потерями энергии за счет джоулева тепла пренебречь.

1.5.32. Определить количество теплоты, которое отводится от нагретого до ϑ_макс = 100°С тела с помощью алюминиевого прямо угольного (40×5 мм) длиной l=5 см охлаждающего ребра Средний коэффициент теплоотдачи с его поверхности k_т = 13 Вт/(м²·К), теплоотдача происходит в спокойный воздух с ϑ₀=35°С, а теплопроводность алюминия λ =200 Вт/(м·К). Найти температуру "холодного" торца" ребра.

Решение. Для расчета теплопередачи вдоль стержня ограниченной длины используем формулу (1.71) для x=l. Тогда

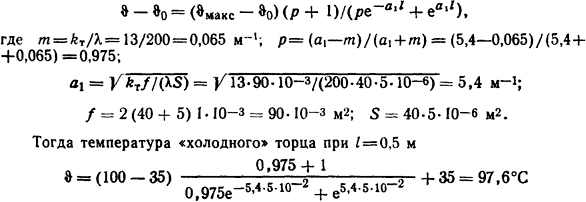
Тепловой поток, который отводится ребром охлаждения, определим из формулы (1.72)

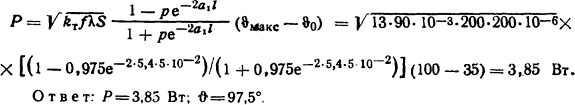
Ответ: Р = 3,85 Вт; ϑ = 97,5°.

1.5.33. Определить длину стального стержня, с поверхности которого рассеивается 80% теплового потока, если его поперечные размеры равны 5×4 мм, а на торце поддерживается постоянная температура ϑ_макс =150°С. Определить значение этого

потока, если коэффициент теплоотдачи с поверхности стержня k_т=10 Вт/(м²·К), температура окружающего воздуха ϑ₀=35°С. Теплопроводность стали λ=40 Вт/(м·К).

1.5.34. Определить допустимое значение тока, который можно длительно пропускать через маслонаполненный реостат, сопротивление которого R=1 Ом при 0°С. Охлаждающая площадь поверхности элементов сопротивления F₁ =2000 см². Элементы сопротивления изготовлены из нихрома, коэффициент теплоотдачи от поверхности которых к маслу k_т1 = 70 Вт/(м²·К), коэффициент теплоотдачи от масла к поверхности бака k_т2=50 Вт/(м²·К). Бак реостата изготовлен из чугуна, его наружная поверхность снабжена ребрами охлаждения в количестве n=20. Каждое ребро охлаждения представляет собой прямоугольную пластину, площадь поперечного сечения которой 100×5 мм, а длина вдоль распространения теплового потока l=40 мм. Площадь охлаждающей поверхности бака, исключая поверхность ребер, F₂==2000 см². Толщина стенки бака δ=5 мм, коэффициенты теплоотдачи с поверхности бака и ребер охлаждения k_т3=10 Вт/(м²·К). При расчете принять допустимую температуру масла ϑ_доп=90°С, теплопроводность чугуна λ = 45 Вт/(м·К). Бак находится в воздухе, температура которого ϑ₀=35°C.

Решение. Составим эквивалентную схему замещения (рис. 1.21). Предположим, что максимальная температура у основания ребер охлаждения и температура наружной поверхности бака равны. В схеме замещения ϑ_м - температура масла в удаленных от элементов сопротивления местах; ϑ_с1, ϑ_с2- температура внутренней и наружной поверхностей стенки бака; Ρ - тепловой поток; R_т1 = 1/(k_т1F₁) = 1/(70·2000·10^-4) =0,0715 К/Вт - тепловое сопротивление теплоотдачи от элементов сопротивления маслу.

Предположим, что S₁=F₃ = F₂+20·5 = 2100 см². Здесь 20·5 - площадь поперечных сечений всех ребер охлаждения. Такое допущение, вероятно, не внесет больших погрешностей; R_т2=1/(л_т2F₃) = 1/(50·2100·10^-4) =0,095 К/Вт- тепловое сопротивление теплоотдачи от масла к поверхности стенки бака; R_т3 = δ/(λS₁) =5·10^-3/(45·2100·10^-4) =0,00053 К/Вт - тепловое сопротивление стенки бака; R_т4=1/(k_т3F₂) = 1/(10·2000·10^-4) =0,5 К/Вт - тепловое сопротивление теплоотдачи от наружной поверхности бака окружающему воздуху;

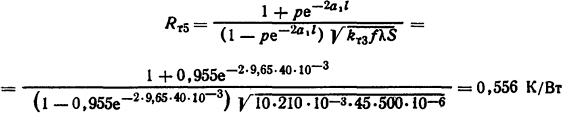
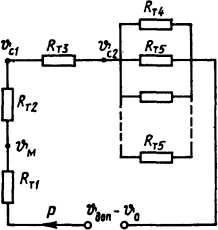
Рис. 1.21. Тепловая схема замещения реостата

-тепловое сопротивление ребра охлаждения, определенное из тaбл. П.13,

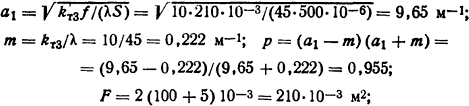
f - площадь охлаждающей поверхности 1 м длины ребра охлаждения; S = 100·5·10^-6 = 500·10^-6 м² - поперечное сечение ребра; λ=45 Вт/(м·К) (см. табл. П. 7).

Используя схему замещения (см. рис. 1.21), вычисляем суммарное тепловое сопротивление: R_ΤΣ = 0,103 К/Вт. Тогда ϑ_доп - ϑ₀ = РR_ΤΣ. Так как Р = I²R₀(1+α ϑ), то

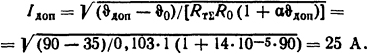
Ответ: I_доп = 25 А.

1.5.35. Рассчитать допустимый ток в реостате для условий задачи 1.5.34, считая, что ребра охлаждения отсутствуют. Остальные данные остались без изменения.

1.5.36. Определить максимальную температуру двух медных цилиндрических стержней, образующих торцовый контакт. Переходное сопротивление контакта R_конт = 2·10^-5 Ом. Диаметры стержней одинаковы: d=20 мм, а длина их бесконечна. Начертить график распределения температур вдоль стержней, если коэффициент теплоотдачи с боковой поверхности стержней окружающему воздуху k_т=15 Вт/(м²·К), температура окружающего воздуха ϑ₀ = 35°С, ток, протекающий по стержням, I=850 А. Теплопроводность меди λ = 390 Вт/ (м·К), удельное сопротивление принять независимым от температуры и равным ρ = 2·10^-8 Ом·м.

1.5.37. Определить температуру поверхности алюминиевой шины в точке, находящейся в середине между двумя контактами, расположенными друг от друга на расстоянии l=200 мм (шина имеет прямоугольное сечение, размеры ее 40×5 мм). Сопротивление каждого контакта R_конт = 6·10^-5 Ом. По шине протекает ток I=550 А. Шина находится в спокойном воздухе, температура которого ϑ₀ = 35°C, коэффициент теплоотдачи с ее поверхности k_т=12 Вт/(м²·К). Теплопроводность алюминия λ = 200 Вт/(м·К), его удельное сопротивление принять равным ρ = 3·10^-8 Ом·м.

1.5.38. Медный круглый стержень, используемый в качестве токоведущего элемента выключателя, имеет резко изменяющееся сечение от диаметра d₁ = 30 мм до диаметра d₂=20 мм. По стержню протекает постоянный ток I=1000 А. Определить максимальную и минимальную установившуюся температуру стержня, а также температуру в месте резкого изменения диаметра,

если стержень находится в спокойном воздухе, температура которого ϑ₀ = 35°С. Коэффициент теплоотдачи с поверхности большего сечения k_T1=S Вт/(м²·К), с поверхности меньшего сечения £-2 = 30 Вт/(м²·К). Теплопроводность меди λ= = 390 Вт/(м·К), ее удельное сопротивление принять равным ρ = 2,0·10⁸ Ом·м. Использовать формулы для расчета нагрева стержня с внутренними источниками теплоты, имеющего резко изменяющееся поперечное сечение [см. формулы (1.81), (1.82) и (1.83)].

1.5.39. Алюминиевая шина прямоугольного сечения, размеры которой 80×6 мм, соединена встык с алюминиевой шиной, имеющей размеры поперечного сечения 50x6 мм. Определить температуру стыка шин при установившемся режиме нагрева, а также температуру узкой шины на расстоянии l=10 см от места стыка, если по шине протекает постоянный ток I=1200 А. Шина находится в воздухе, температура которого ϑ₀=35°C, коэффициент теплоотдачи с большей поверхности шины ,fc-i = 20 Вт/(м²·К), с меньшей поверхности k_Т2=25 Вт/(м²·К). Теплопроводность алюминия λ=200 Вт/(м·К), удельное сопротивление принять равным ρ = 2,9·10^-8 Ом·м. При решении считать, что шина имеет неограниченные в обе стороны линейные размеры.

1.5.40. Бесконечно длинный медный круглый токопровод диаметром d=30 мм на длине l= 30 мм имеет заточку до диаметра d₁=20 мм. Токопровод находится в воде, температура которой ϑ₀ = 20°С. Коэффициенты теплоотдачи с тонкой части токопровода k_т1=200 Вт/(м²·К), с толстой k_т2=100 Вт/(м²·К), теплопроводность меди λ=390 Вт/(м·К), удельное электрическое сопротивление принять равным ρ=2,1· 10^-8 Ом·м. По токопроводу протекает переменный ток I=4000 А частоты f=50 Гц. Определить максимальную температуру узкой и широкой частей токопровода.

1.5.41. Медная шина круглого сечения диаметром d = 30 мм бесконечной длины имеет утолщение, диаметр и длина которого соответственно равны d₁=40 мм, l=400 мм. По шине протекает постоянный ток I=1500 А. Коэффициенты теплоотдачи с боковых поверхностей толстой части шины k_т1=20 Вт/(м²·К), тонкой k_т1 = 30 Вт/(м²·К). Определить минимальную температуру в шине и температуру шины в месте стыка. Теплопроводность меди λ = 390 Вт/(м·К), ее удельное электрическое сопротивление принять равным ρ = 2,0·10^-8 Ом·м, температура окружающей среды ϑ₀=35°0.

1.5.42. Длинная стальная шина прямоугольного сечения размером 30×3 мм расположена в спокойном воздухе, температура которого ϑ₀ = 35°С. В средней части шина имеет утолщение длиной l=50 мм и поперечным сечением 40×6 мм. Коэффициенты теплоодачи с поверхности шины и утолщения равны k_т2= = 10 Вт/(м²·К). Определить температуру в середине утолщения и в месте изменения поперечного сечения, если по шине протекает

постоянный ток I=150 А. Теплопроводность стали λ = 40 Вт/(м·К), ее удельное электрическое сопротивление ρ = 12·10^-8 Ом·м.

1.5.43. Определить максимальную и минимальную темпера туру магнитопровода катушки индуктивности, которая намота на на ферромагнитный сердечник, изготовленный из листово трансформаторной стали марки 1512 с толщиной листов δ = 0,5 мм. Высота катушки h=170 мм, число витков N=250, по ней протекает переменный ток I=20 А. Поперечное сечение маг нитопровода 70x70 мм, длина его средней линии l_cp=720 мм. Между катушкой и магнитопроводом отсутствует теплообмен, катушка находится в воздухе, температура которого ϑ₀ = 35°С Коэффициент теплоотдачи с наружных частей магнитопровод k_т=10 Вт/(м²·К).

1.6. Тепловой расчет электрических аппаратов и их частей с учетом совместного действия теплопроводности, конвекции и излучения