Простейшие методы расчета нагрева я охлаждения электрических аппаратов и их частей 8 страница

2.3.8. Определить усилия, действующие на каждый из ножей трехполюсного разъединителя, по которому протекает предельный сквозной ток трехфазного к.з. Амплитудное значение тока I_макс = 320 кА, длина ножей l=610 мм, расстояние между ними h=700 мм. Вычислить также требуемый момент сопротивления ножей.

Решение. В соответствии с выводами, приведенными в [1], на каждый из ножей в случае установившегося тока к.з. будут действовать знакопеременные во времени усилия. Определим максимальные притягивающие и максимальные отталкивающие усилия на каждый из трех ножей разъединителя (рис. 2.14):

В соответствии с формулой (2.15)

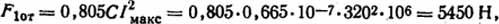
где C=μ₀k_1/2/(4π)==4π10^-7·0,665/(4π)=0,665·10^-7. Из табл. п.18 k_1/2=0,665; по формуле (2.17) F_1пр=0,055СI²_макс=374 Н, где С = μ₀k_1/2/(4π). Аналогично, F_2от=F_2пр=0,87CI²_макс=5900 Η; F_3от=F_1от=5450 Н; F_3пр=F_1пр=374 H.

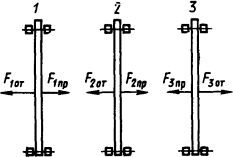
Рис. 2.14. Эскиз разъединителя поперечного сечения

Наиболее напряженным будет средний полюс, поэтому его необходимо рассчитывать на прочность изгиба как балку на двух опорах. Требуемое значение момента сопротивления поперечного сечения

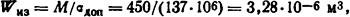
где M=F_максl/8= 5900·0,61/8 =450 Н·м - изгибающий момент; σ_доп=137×10⁶ Па - допустимое напряжение на изгиб для ножей, выполненных из меди.

Ответ: F_1от = F_3от = 5450 Η; F_1пр = F_3пр=374 Η; F_2от = F_2пр =5900 Н; W_из = 3,28·10^-6 м³.

2.3.9. Вычислить электродинамические усилия, воздействию которых подвергаются три ножа трехполюсного разъединителя. Через ножи протекает ток трехфазного к.з. промышленной частоты f=50 Гц, максимальное значение которого I_макс = 80 кА. Расстояние между полюсами разъединителя данного типа h = 450 мм, длина ножей l=635 мм. При расчете пренебречь влиянием апериодической составляющей тока к.з.

2.3.10. Для условий задачи 2.3.9 подобрать требуемое по прочности и жесткости сечение ножей, приняв, что каждый нож состоит из двух медных пластин, жестко закрепленных в нижней части разъединителя и свободно опирающихся в верхней части, где имеются подвижные размыкающие контакты. При расчете на жесткость исходить из условия, что частота собственных колебаний ножей должна быть меньше двойной частоты сети.

2.3.11. На каком минимальном расстоянии можно поставить опорные изоляторы в распределительном устройстве, если в нем применены прямоугольные медные шины сечением 100×10 мм по одной шине на фазу. Шины закреплены жестко на опорах, поставлены на ребро и по ним протекает ток трехфазного к.з., установившееся значение которого I_уст=50 кА. Расстояние между фазами равно 0,3 м.

Решение. Определим значение электродинамического усилия, действующего на 1 м длины шин, при этом расчетное значение тока определим по формуле (2.14)

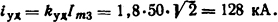
Здесь k_уд =1,8.

Сила, действующая на 1 м длины,

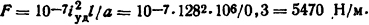
Для многопролетной балки [1]

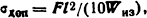
где W_из=bh²/6 - момент сопротивления поперечного сечения шины; σ_доп = 13,7·10⁷ Н/м² - допустимое напряжение на изгиб для меди.

Подставив числовые значения, получим

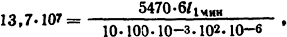
откуда l_1мин=0,65 м.

Поскольку по шинам протекает переменный ток, необходимо найти минимальное расстояние между изоляторами в случае отсутствия механического резонанса. При этом собственная частота шин должна быть меньше частоты механических колебаний, т.е. двойной частоты тока.

Из формулы [1]

где k=112 для жесткого закрепления шин; E=11,8·10⁶ Н/см² - модуль упругости для меди; J = bh³/12=10·1³/12 = 0,838 см⁴ момент инерции сечения шины; γ = 85,2 Н/см³ - удельный вес меди; S = 10 см² - поперечное сечение шины.

После решения равенства (а) относительно l_2мин получаем требуемое расстояние между изоляторами l_2мин=0,596 м. Выбираем наименьшее из двух полученных значений, т.е. 0,6 м.

Ответ: l_мин=0,6 м.

2.3.12. Решить задачу 2.3.11 при условии, что шины расположены плашмя. Остальные данные без изменения.

2.3.13. Решить задачу 2.3.11 при условии, что шины круглые, диаметр которых d=35 мм, а все остальные данные остались без изменения.

2.3.14. Определить максимальные напряжения, возникающие в наиболее нагруженном пакете шин распределительного устройства трехфазного генератора, если короткое замыкание произошло на выходе из распределительного устройства и действующее значение установившегося тока трехфазного к.з. I_уст = 140 кА. Пакеты шин расположены в одной плоскости, расстояние между ними h=700 мм, расстояние между опорными изоляторами l=600 мм, пакеты шин состоят из 2-х жестко связанных медных шин с размерами поперечного сечения 120×10 мм, расстояние между шинами пакета d=10 мм и через каждые 10 см между шинами имеются прокладки.

Решение. При вычислении напряжения на изгиб необходимо учесть взаимодействие между шинами пакета, т.е. σ_расч = σ_фаз+σ_пак, где σ_фаз - напряжение от усилий, возникающих от взаимодействия соседних фаз; σ_пак - напряжение от взаимодействия шин в одном пакете.

Поскольку наиболее напряженным при данном расположении шин будет средний пакет шин, для него и проведем расчет. Максимальное усилие, действующее на средний пакет,

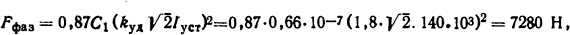
где C₁ = μ₀k₁/(4π)=0,66·10^-7; k_уд=1,8 - ударный коэффициент, учитывающий влияние на электродинамические усилия апериодической составляющей тока к.з. Так как короткое замыкание произошло вблизи генератора, то это влияние довольно значительно. Так как шину можно рассчитать как многопролетную балку [1], то σ_фаз=F_фазl/(10W_из)=7280·0,6/(10·1,44·120·10^-3·10²·10^-6) =25,3·10⁶ Па, где W_из = 1,44ab² - момент инерции поперечного сечения пакета шин [13]; а=120 мм; b=10 мм.

Максимальное усилие, возникающее между шинами пакета, можно вычислить как максимальное усилие в однофазной системе, и так как шины в пакете находятся близко друг к другу, то необходимо учесть влияние конечных

размеров шин. Предположим, что ток между шинами пакета распределен равномерно. Тогда

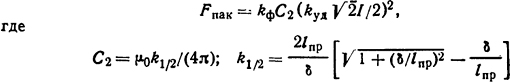
(см. табл. П. 18); l_пр=100 мм - расстояние между прокладками; δ = 20 мм - расстояние между осями шин; k_ф = 0,4 - коэффициент формы (см. рис. П. 12). После вычислений получим С₂ = 8·10^-7.

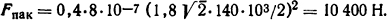
Напряжение изгиба в пакете шин [1]

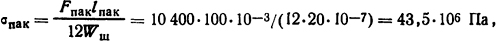
где W_ш=ab²/6=120·10³·10^-2·10^-6/6 = 20·10^-7 м³. Суммарное максимальное напряжение изгиба в наиболее нагруженной шине σ=σ_фаз+σ_пак = 25,3·10⁶+43,5·10⁶ = 68,8·10⁶ Па.

Ответ: σ=68,8·10⁶ Па.

2.3.15. Вычислить максимальные напряжения в наиболее нагруженном пакете шин распределительного устройства трехфазного синхронного генератора для случая трехфазного к.з., действующее значение тока которого в установившемся режиме I_уст = 50 кА. Пакеты шин расположены в одной плоскости, расстояние между ними h=450 мм, расстояние между опорными изоляторами l=500 мм; пакеты шин состоят из двух жестко связанных алюминиевых шин размером 50×5 мм, расстояние между шинами в пакете 5 мм и через каждые 20 см между шинами пакета имеются прокладки. При расчете учесть влияние апериодической составляющей тока к.з.

ГЛАВА 3. ЭЛЕКТРИЧЕСКАЯ ДУГА И ЕЕ ГАШЕНИЕ

3.1. Физические параметры дуговой плазмы

В этом параграфе приведены задачи по некоторым исходным физическим параметрам и связи между ними (например, определение длины свободного пробега электрона в дуговой плазме и ее зависимости от температуры и давления газа, энергии электрона, степени ионизации газа с помощью уравнения Саха, решение вопроса рекомбинации ионизированных частиц и передачи энергии от дугового столба к окружающей газовой среде). Решение таких задач дает возможность ознакомиться с некоторыми физическими закономерностями и числовыми значениями наиболее употребительных величин в теории газового разряда высокого давления. При этом используются следующие формулы и соотношения.

Длина (см) свободного пробега электрона.

где N_Т - число молекул в 1 см³ газа при температуре Т; d - диаметр молекулы газа, см.

Средняя энергия электронов (эВ), ускоряемых в электрическом поле напряженностью Ε (В/см),

Мощность, отводимая в воздухе с 1 см длины дуги путем теплопроводности,

где Т - температура дуги, К.

Мощность, отводимая от 1 см длины дуги путем поперечной конвекции,

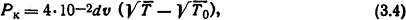
где T - температура дуги, К; T₀ - температура окружающей среды, К; v - скорость поперечного потока воздуха, м/с; d - диаметр столба дуги, см, определяемый по формуле

где I - ток в дуге, А.

Формула Саха

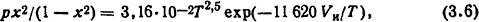
где p - давление газа, Па; x - относительная ионизация в долях единицы, V_и - энергия ионизации, эВ; Т - температура, К.

Начальная скорость спада плотности ионов в ионизированном газе за счет рекомбинации

где α - коэффициент рекомбинации.

3.1.1. Определить среднюю длину пробега электрона в азоте при атмосферном давлении и температуре газа T=5000 К.

Решение. Длина свободного пробега электрона определится из (3.1), где d=3,146·10^-8 см - диаметр молекулы азота (см. табл. П.22). Для нахождения λ_э необходимо знать Ν_т. Известно, что число молекул любого газа в 1 см³ при атмосферном давлении и 0°С N₀=2,7·10¹⁹ см^-3.

Определим Ν_т, считая, что число частичек газа в 1 см³ (плотность газа) при температуре Т находится в обратном отношении абсолютных температур, т.е. Ν_т=Ν₀Τ₀/Т =2,7·10¹⁹·273/5000= 14,74·10¹⁷ см^-3, тогда средняя длина свободного пробега электрона из (3.1)

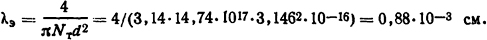
Ответ: λ_э=0,88·10^-3 см.

3.1.2. Определить среднюю длину свободного пробега электрона в атмосфере кислорода при давлении p=2·10⁵ Па и температуре T=7000 К.

3.1.3. Определить среднюю длину свободного пробега электрона в атмосфере водорода при давлении р = 3·10⁵ Па, температуре Т = 8000 К.

3.1.4. Определить среднюю энергию электрона в азоте, приобретаемую им в электрическом поле напряженностью Е = 50 В/см при температуре газа Т = 10000 К и давлении газа р=9,8·10⁴Па.

Решение. Если заряд электрона принять за единицу, то средняя энергия электронов, ускоряемых в электрическом поле напряженностью E, определится из (3.2)

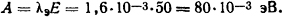
Здесь λ_э = 4/(πN_тd²) =4/[3,14·7,37·10¹⁷(3,146)²·10^-16] = 1,6·10^-3 см - средняя длина свободного пробега электрона в азоте, Ν_т = Ν₀Τ₀/Τ=2,7·10¹⁹·273/10000 = 7,37·10¹⁷; d=3,146·10^-8 (см. табл. П.22).

Ответ: A_э=80·10^-3 эВ.

3.1.5. Определить среднюю энергию электрона в атмосфере азота, приобретенную им в электрическом поле напряженностью E=100 В/см при температуре газа T=10000 К и давлении р = 3·10⁵Па.

3.1.6. Определить среднюю энергию электрона в атмосфере водорода, приобретенную им в электрическом поле напряженностью E=100 В/см при температуре газа T=18000 К и давлении р = 5·10⁵Па.

3.1.7. Определить мощность, отводимую поперечным потоком воздуха, скорость которого v = 3 м/с. Температура газа в дуговом столбе Т=5000 К, температура окружающей среды T₀=300 К. Ток в дуге I=50 А. Полученный результат сопоставить с мощностью, отводимой за счет теплопроводности в воздухе.

Решение. Мощность, отводимая в воздухе с 1 см длины дуги путем теплопроводности, в соответствии с (3.3)

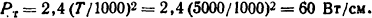
Диаметр дугового столба при относительной скорости движения его в среде определим по формуле Брона

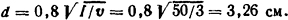
Мощность, отводимая за счет конвекции [см. (3.4)],

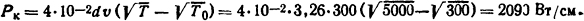
Ответ: Р_к = 2090 Вт/см.

3.1.8. Оценить мощность, отводимую от дугового столба длиной в 1 см путем излучения, если ток в дуге I=5000 А, напряженность поля E=80 В/см. Электроды выполнены из меди.

3.1.9. Определить мощность, отводимую от дугового столба длиной в 1 см за счет теплопроводности. Температура T=7000 К.

3.1.10. Определить мощность, отводимую от дугового столба длиной в 1 см путем конвекции газа (азота). Скорость движения дуги v=25 м/с, температура газа в дуговом столбе T=8000 К, температура окружающей среды Т = 500 К.

3.1.11. Оценить мощность, отводимую с 1 см длины дуги путем конвекции, при условии, что температура столба дуги Т= 3000 К, температура окружающей среды Т=320 К, диаметр - дуги d=l,5 см, скорость проникновения (средняя) холодного потока газа в дуговой столб v = 50 м/с.

3.1.12. Оценить и сравнить долю общей рассеиваемой дуговым столбом мощности по существующим эмпирическим формулам. Ток дуги I=5000 А, падение напряжения в столбе U = 200 В/см.

3.1.13. Вычислить и построить кривую мощности дуги длиной l=5 см за полупериод переменного тока при условии, что ток в дуге изменяется по закону i =450 sin ωt, а напряжение на дуге

3.1.14. Какая часть от общего числа частичек газа находится в ионизированном состоянии при условии, что энергия ионизации атома газа V_и=15 эВ, температура газа T=12000 К, давление p=4·10⁵ Па?

Решение. Связь между относительной ионизацией газа, его температурой Т, энергией ионизации V_и и давлением p можно выразить с помощью уравнения Саха (3.6). Обычно полагают, что x≪1, и поэтому

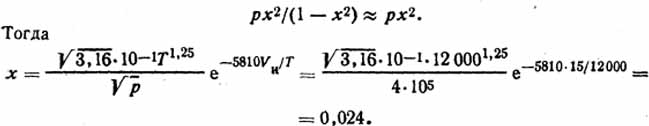
Ответ: х=0,024.

3.1.15. Определить начальную скорость спада плотности ионов в ионизированном газе за счет рекомбинации, а также плотность ионов спустя 10 мкс с начала процесса, если коэффициент рекомбинации α = 10^-9 и начальная плотность ионов в остаточном столбе n₀=10¹⁵.

Решение. Начальную скорость спада плотности ионов определим по формуле (3.7)

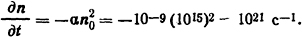
Решение уравнения (3.7) дает зависимость n=n(t), т.е. плотность ионов спустя время t. Для t=10^-5 с будем иметь n=n₀/(1+n₀αt) = 10¹⁵/(1 + 10¹⁵·10^-9·10^-5)=0,91·10¹⁴ пар ионов.

Ответ: dn/di= -10^-21 с^-1; n=0,91·10¹⁴ пар ионов.

3.1.16. Определить начальную скорость спада плотности ионов в ионизированном газе дугового столба, если коэффициент рекомбинации газа α=10^-9, начальная плотность ионов n₀=10¹⁵.

3.1.17. Построить для частного случая зависимость спада во времени плотности ионов в дуговом столбе за счет рекомбинации ионов. Коэффициент рекомбинации газа α=2·10^-9, начальная плотность ионов n₀ = 10¹⁵.

3.2. Электрическая дуга в магнитном поле

В этом параграфе приведены задачи оценки некоторых характеристик дуги в магнитном поле. Рассматриваются также задачи на движение дуги в узких щелях дугогасительных камер. Между дуговым столбом и магнитным

полем возникают силы взаимодействия, под влиянием которых дуговой столб приходит в движение. Явления сообщения дуговому столбу значительных скоростей широко используют в отключающих аппаратах с целью повышения интенсивности гашения дуги, а также для повышения срока службы аппаратов. При решении задач используются следующие расчетные формулы и соотношения.

Скорость перемещения дуги в результате действия тока в шинах при В ≤ 0,1 Тл определяется по формуле Г.А. Кукекова

где I - ток в дуге, А; В_ср - магнитная индукция между шинами, Тл.

Скорость движения дуги в результате действия тока в шинах, по данным О.Б. Брона, определяется по формуле

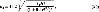
где Η - напряженность магнитного поля, А/см.

Скорость дуги, находящейся в узкой щели, по данным Г.А. Кукекова, определяется по формуле

где δ - ширина щели, м; I - ток в дуге, А; В - величина индукции, Тл.

3.2.1. Определить скорость дуги между круглыми медными шинами диаметром d=20 мм, по которым протекает ток I_д=1500 А. Расстояние между шинами δ=10 мм. Шины находится в воздухе, магнитная проницаемость которого μ₀=4 π10^-7 Гн/м.

Решение. Для определения скорости смещения дуги между шинами необходимо знать значения магнитной индукции между шинами. Примем за расчетное значение индукции ее величину в средней точке между шинами, т.е.

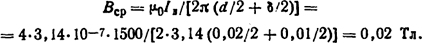
По формуле Кукекова (3.8), скорость перемещения дуги от тока в шинах

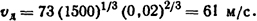
Ответ: v_д=61 м/с.

3.2.2. Определить скорость движения дуги в средней (между электродами) ее зоне между круглыми шинами, имеющими диаметр d=10 мм, при токе в шинах I=2000 А и расстоянии между ними 10 мм.

3.2.3. Определить скорость движения открытой (свободной) дуги с током I_д = 400 А, находящейся в поперечном магнитном поле с индукцией B = 0,05 Тл.

Решение. Для индукций в пределах 0<В<0,1 Тл по формуле Кукекова (3.8)

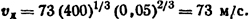
По формуле Брона (3.9) скорость движения дуги

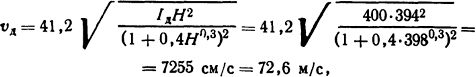
где H=B/μ₀=0,05/(4π·10^-7)=39800 А/м = 398 А/см.

Сопоставив полученные результаты, получим среднее значение V_СР=0,5 (73 + 72,6) =72,8 м/с.

Ответ: v_cp=72,8 м/с.

3.2.4. Магнитная индукция равномерного магнитного поля B = 0,07 Тл. Определить скорость перемещения дуги с током I = 500 А, находящейся в этом магнитном поле.

3.2.5. Определить скорость перемещения свободной дуги с током 600 А, находящейся в магнитном поле, создаваемом тем же током дуги, если число витков катушки магнитного дутья N = 4 и расстояние между полюсами (воздушный зазор) δ = 20 мм.

3.2.6. Определить скорость перемещения дуги в узкой щели дугогасительной камеры при условии, что поперечное магнитное поле в камере создается катушкой, имеющей N=10 витков и обтекаемой током дуги I_д=400 А. Ширина щели (рис. 3.1), в которую затягивается дуга, δ = 2 мм. Расстояние между полюсами катушки (воздушный зазор) Δ = 2 см.

Решение. По формуле Кукекова (3.10) скорость дуги, находящейся в узкой щели,

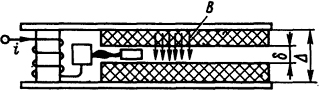
Рис. 3.1. Эскиз катушки магнитного дутья

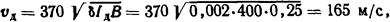
где В - индукция в камере;

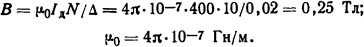
Ответ: v_д=165 м/с.

3.2.7. Определить скорость перемещения дуги в узких щелях между изоляционными пластинами, если расстояние между ними δ = 3 мм, индукция в щелях B = 0,15 Тл и ток в дуге I_д=500 А.

3.2.8. Определить скорость перемещения электрической дуги постоянного тока на концентрических кольцах, имеющих между собой зазор 1 см, при условии, что дуга вместе с кольцами находится в длинной однослойной катушке (N=1000 витков), а ток, протекающий по виткам, I = 50 А.

Решение. Найдем индукцию в средней зоне катушки:

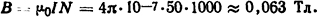
Для такой индукции можно использовать формулу Кукекова (3.8), она справедлива для B<0,1 Тл:

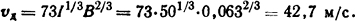
Ответ: v_д = 42,7 м/с.

3.2.9. Определить скорость перемещения дуги между концентрическими кольцами, помещенными в полость катушки постоянного тока. Катушка большой длины имеет 1000 витков на 1 м и ток в ее обмотке I=100 А. Зазор между кольцами 10 мм, ток в дуге I_д= 100 А.

3.2.10. Определить направление и значение скорости перемещения электрической дуги, образующей круговое кольцо, под влиянием собственного поля при радиусе дугового кольца R = 30 см, токе в дуге I_д=500 А и радиусе дугового столба r=0,03 √I_д.

3.2.11. Определить время, за которое дуга, имеющая вид кольца, переместится (растянется) из положения радиуса R₁ = 30 см до положения R₂=70 см при токе в дуге I_д = 1500 А (радиус дугового столба выбирают из условия, приведенного в задаче 3.2.10).

3.2.12. Определить скорость, с которой дуговой столб будет удаляться от параллельного ему проводника, обтекаемого тем же током I=2500 А. Расстояние между дуговым столбом и проводом (между их осями) составляет 15 см.

3.3. Дуга постоянного тока

В этом параграфе рассмотрены задачи на определение времени угасания дуги постоянного тока, критических длин и токов дуги, а также энергии, поглощаемой дугой во время ее гашения. Дана оценка ожидаемых перенапряжений при срезах токов, роли шунтирующих сопротивлений, подсоединяемых к дуге постоянного тока, и индуктивности, находящейся в рассматриваемом контуре последовательно с отключающим промежутком. При этом используются следующие расчетные формулы и соотношения.

Энергия горения дуги

где U_д, i - соответственно падение напряжения на дуге, В, и ток в дуге, А; t_д - время горения дуги, с. Время горения дуги

где L - индуктивность цепи, Гн; ΔU - перенапряжение, В; I - установившийся ток цепи, А.

Вольт-амперная характеристика дуги

где i - ток дуги, А; l - длина дуги, м, с и a - числовые коэффициенты, определяемые экспериментально.

3.3.1. Определить энергию, поглощенную дугой постоянного тока при ее гашении, если сопротивление отключаемой цепи R=1 Ом, индуктивность цепи L=100 мГн, спад тока имеет прямолинейный характер, время угасания дуги t_д=0,1 с, напряжение цепи U_н=200 В.

Решение. Исходя из уравнения напряжений U_и = iR + U_д + Ldi/dt, получаем выражение энергии дуги в соответствии с (3.11)

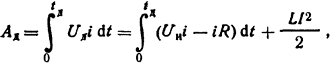
где I=U/R = 200/1=200 А -ток в цепи.

Интеграл в правой части уравнения представляет собой энергию, поглощенную в дуге и подведенную от источника за время горения дуги I_д = 0,1 с. Интеграл может быть вычислен, если задана зависимость изменения тока во времени. По условию задачи, ток в зависимости от времени падает по прямой линии, т.е. i=I(l-t/t_д). Тогда

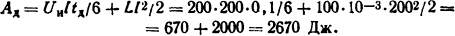
Ответ: A_д=2670 Дж.

Примечание. Из примера видно, что основная доля энергии, поглощенная дугой, определяется энергией, запасенной в индуктивности. Такие соотношения обычно возникают при больших индуктивностях цепи и малом времени горения дуги.

3.3.2. Определить энергию, поглощенную дугой постоянного тока при ее гашении, если напряжение U=200 В, сопротивление R = 1,5 Ом, индуктивность L = 80 мГн, время угасания дуги t_д = 0,09 с, спад тока имеет прямолинейный характер.

3.3.3. Общее количество энергии, поглощенной дугой за один цикл отключения, А=3000 Дж. Оценить, какое количество энергии потребуется из сети непосредственно за время одного отключения; если отключаемый ток (начальный) I = 200 А, индуктивность цепи L = 80 мГн.