Простейшие методы расчета нагрева я охлаждения электрических аппаратов и их частей 9 страница

3.3.4. Определить время угасания дуги постоянного тока для двух случаев индуктивности цепи L=10·10^-3 Гн и L = 0,1·10^-3 Гн при условии, что ΔU=30 В остается величиной постоянной (рис. 3.2). Напряжение источника U_и=400 В, сопротивление цепи R=2 Ом.

Решение. Установившийся ток цепи I= U_и/R = 400/2 = 200 А. Из выражения ΔU=-L

при L = 0,1·10^-3 Гн время угасания дуги по (3.12)

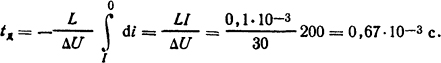
Для L=10·10^-3 Гн время угасания дуги в 100 раз больше, т.е. t_д=67 мс.

Ответ: для 1=0,1·10^-3 Гн t_д=0,67 мс; для L=10·10^-3 Гн t_д=67 мс.

3.3.5. Определить графоаналитическим методом время угасания дуги, если в цепи сопротивление R=3 Ом, индуктивность L=120 мГн, напряжение источника U_и=400 В, а вольт-амперная характеристика описывается уравнением U_д=ci^-al, где l=1,2l_кр; с = 80; a=0,5, l_кр - критическая длина дуги.

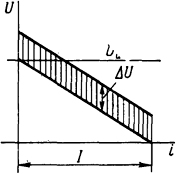
Рис. 3.2. Зависимость напряжения от тока

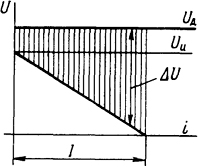
Рис. 3.3. Зависимость напряжения от тока

3.3.6. Определить полное время угасания дуги, если напряжение на дуге U_д=250 В в зависимости от тока остается постоянным (рис. 3.3). Напряжение сети U_и=200 В, сопротивление R = 1 Ом, индуктивность L=15 мГн.

Решение. Полное время горения дуги определим по формуле (3.12).

Значение ΔU=U_д-U_н+iR. Подставив ΔU в выражение для t_д и проинтегрировав его, получим

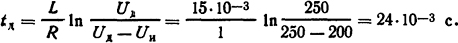
Ответ: t_д = 24·10^-3 с.

3.3.7. Определить время угасания дуги постоянного тока при условии, что напряжение ΔU=35 В остается величиной постоянной в течение всего времени гашения. Напряжение источника U_и=400 В, сопротивление R=4 Ом, индуктивность L = 15·10^-3 Гн.

3.3.8. Определить критическую длину дуги l_кр постоянного тока и критический ток дуги i_кр для цепи с общим сопротивлением R = 1,2 Ом при напряжении источника U_и=400 В. Выражение вольт-амперной характеристики, имеет вид (3.13), где с=80, а =0,5.

Решение. Для такой вольт-амперной характеристики

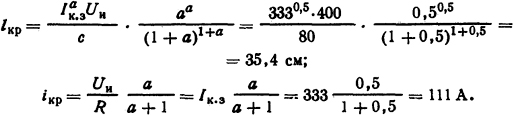
Здесь I_к.з=U_и/R = 400/1,2 = 333 А.

Ответ: l_кр=35,4 см; i_кр=111 А.

3.3.9. Определить критическую длину дуги и ее критический ток, если сопротивление цепи R = 1,5 Ом, напряжение U_и=600 В. Вольт-амперная характеристика описывается уравнением (3.13), где с = 90, а=+0,4.

3.3.10. Установить необходимое число промежутков в решетке, если дуга постоянного тока должна гаситься путем деления ее на ряд коротких дуг. Напряжение цепи U_и=400 В, а напряжение на дуге U_д=500 В остается постоянным.

3.3.11. До какой длины должна растянуться дуга постоянного тока, чтобы достигнуть неустойчивого состояния? Вольт-амперная характеристика дуги описывается уравнением (3.13), где с= 100, а= +0,5. Напряжение сети U_и = 400 В, ток в цепи I = 100 А.

3.3.12. Определить возможное перенапряжение U_макс в цепи постоянного тока, если происходит ее размыкание без дуги, при условии, что к зажимам индуктивности подключена емкость C=0,1 мкФ. Индуктивность в цепи L = 1,5 Гн, ток I=20 А.

Решение. Если пренебречь активным сопротивлением индуктивной катушки, то наиболее ожидаемое напряжение может быть определено из того условия, что вся электромагнитная энергия переходит в электростатическую

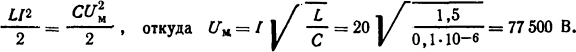
Ответ: U_м = 77500 В.

3.3.13. Определить перенапряжение на индуктивности L = 1,0 Гн при разрыве тока I=25 А без дуги при параллельной емкости С=0,15 мкФ.

3.3.14. В цепи постоянного тока отключается большая индуктивность. Для ограничения перенапряжения эта индуктивность перед разрывом цепи шунтируется сопротивлением. Найти значение этого сопротивления, если отключаемый ток I=300 А, напряжение U=200 В, наибольший пик перенапряжения U_макс = 500B.

3.3.15. Определить значение емкости, которая должна быть подключена параллельно индуктивности L = 1 Гн, с тем чтобы при внезапном обрыве цепи (без дуги) перенапряжение на индуктивности не превышало 10 кВ. Ток цепи, текущий через индуктивность, I=15 А.

3.4. Дуга в коротком промежутке

В настоящем параграфе рассмотрены задачи гашения дуг постоянного и переменного токов малой длины (порядка единиц миллиметра), а также задач, в которых определяются необходимое число пластин в решетке и пробивное напряжение единичного промежутка с учетом и без учета восстановления прочности промежутка в зависимости от времени. При этом используются следующие расчетные формулы и соотношения.

Число пластин дугогасительной решетки

где U - напряжение сети, U_a и U_к - анодное и катодное падения напряжения соответственно.

Амплитуда восстанавливающего напряжения

где k - коэффициент превышения амплитуды. Пробивное напряжение короткого промежутка

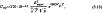
где E_макс - напряженность электрического поля автоэлектронной эмиссии, В/см; Т - температура газа, К; V_н - энергия ионизации, эВ; ρ - давление тазовой среды, Па.

Начальная прочность короткого промежутка

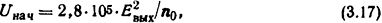
где Е_вых - напряженность поля выхода электронов, В/см; n₀ - плотность носителей зарядов после перехода тока через нуль.

Закон изменения плотности ионов во времени

где n₀ - начальная плотность ионов; α - коэффициент рекомбинации.

3.4.1. Определить число стальных пластин решетки аппарата постоянного тока для гашения дуги, возникающей на его контактах, при напряжении U=440 В.

Решение. Дуга, входящая в стальную решетку под влиянием магнитных сил, в средней зоне пластин останавливается, в результате чего образуются сильно нагретые электроды дуги. Сумма катодного и анодного напряжений получается сравнительно небольшой: U_a+U_к≈20... 25 В. Таким образом, число пластин решетки в соответствии с (3.14) m=U/(U_a+U_к) + 1 = 440/20+1=23.

Если расстояние между пластинами 0,1 см, то общее напряжение на дуге U_д=0,1·22·I_д=2,2·20=44 В. Это значение напряжения может пойти в запас надежности работы аппарата.

Примечание. При решении подобных задач для нахождения числа пластин решетки из медных пластин при быстром движении дуги сумма катодного и анодного напряжений может быть повышена до 50 В и, следовательно, при тех же параметрах число пластин составит уже примерно 10 шт.

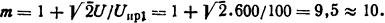
Ответ: m = 23.

3.4.2. Определить число медных пластин решетки дугогасительного аппарата переменного тока, если восстановление напряжения на промежутке происходит с очень высокой скоростью. При этих условиях следует принять пробивное напряжение для единичного промежутка U_пр1=200 В. Рабочее напряжение цепи 600 В (действующее) .

Решение. При ряде последовательных промежутков пробивное напряжение между пластинами распределяется неравномерно. При расчетах

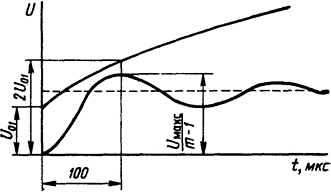
Рис. 3.4. Осциллограмма напряжения

следует принимать среднее значение пробивного напряжения в 1,5... 2 раза меньше, т.е. U_пр1 = 100 В. Тогда число пластин решетки в соответствии с (3.14)

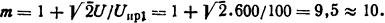
Ответ: m=10.

3.4.3. Сколько следует взять стальных пластин решетки для гашения дуги в цепи переменного тока с напряжением U=600 В с током отключения I = 100 А?

3.4.4. Сколько пластин следует взять для медной решетки, если номинальное напряжение сети переменного тока U=600 В, отключаемый ток I=200 А? Дуга на пластинах перемещается магнитным полем.

3.4.5. Определить число стальных пластин в решетке, учитывая, что прочность должна быстро нарастать во времени и через 100 мкс должна увеличиться в 2 раза по сравнению с начальной величиной (рис. 3.4). Действующее значение напряжения U=600 В. Напряжение восстанавливается с частотой f₀=5000 Гц. Коэффициент превышения амплитуды k =1,4. Начальное расчетное пробивное напряжение единичного промежутка U_пр1 = 120 В.

Решение. Амплитуда восстанавливающегося напряжения определяется по формуле (3.15)

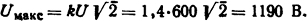
Через 100 мкс (прочность единичного промежутка U_пр=U_пр1·2=120·2=240 В.

При f₀=5000 Гц полупериод собственной частоты τ=1/(2f₀) = 1/(5000·2)=1/10000 с= 100 мкс.

Известно, что через этот отрезок времени прочность единичного промежутка достигает 240 В, а амплитуда восстановления напряжения достигает 1190 В. Отсюда при 20%-ном запасе число пластин в решетке в соответствии с (3.14)

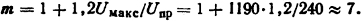
Ответ: m=7.

3.4.6. Определить число стальных пластин дугогасительной камеры, если начальная прочность единичного промежутка U_пр1 = 120 В, частота росстановления напряжения f₀=1000 Гц, коэффициент превышения амплитуды восстанавливающегося напряжения k=l,6. Рабочее возвращающееся напряжение на

разрыв U_в = 600 В. Известно также, что за 50 мкс прочность промежутка достигает двойной величины по сравнению с начальной.

3.4.7. По какому закону должен спадать ток в обмотке возбуждения генератора, если обмотка возбуждения замкнута на дуговой промежуток с медными пластинами и напряжение на нем в основном складывается из суммы анодных и катодных падений напряжений?

3.4.8. Определить число пластин в камере автомата гашения поля генератора, если во время гашения поля она замкнута на дуговой промежуток с медными пластинами. Индуктивность обмотки возбуждения генератора f=0,5 Гн, начальный ток возбуждения I=1000 А, а наибольшее напряжение на обмотке генератора U_макс = 600 В.

3.4.9. Определить пробивное напряжение дугового короткого промежутка, если напряженность электрического поля автоэлектронной эмиссии U_макс = 5·10⁵ В/см, температура газа Т=5000 К, энергия ионизации частиц V_и=H эВ, давление газовой среды p =4·10⁵ Па.

Решение. Связь пробивного напряжения короткого промежутка с указанными величинами определяется выражением (3.16)

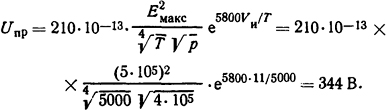
Ответ: U_пр=344 Β.

3.4.10. Определить электрическую прочность короткого промежутка, если напряженность" электрического поля автоэлектронной эмиссии U_макс = 5,5·10 В/см; температура газа Г=6000 К, энергия ионизации частиц V_и=11,5 эВ, давление газовой среды р = 3·10⁵Па.

3.4.11. Определить начальную прочность короткого промежутка, если плотность носителей зарядов в дуговом промежутке непосредственно после перехода тока через нуль n₀ = 5·10¹⁵ см^-3, напряженность поля выхода электронов E_вых=2·10⁶ В/см.

Решение. Связь между значением пробивного напряжения U_пр, плотностью ионов n₀ и напряженностью поля выхода Е_вых. можно выразить формулой (3.17) и тогда

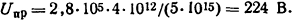
Ответ: U_пр=224 В.

3.4.12. Определить пробивное напряжение короткого промежутка сразу после перехода тока через его нулевое значение и

спустя 10 и 50 мкс. Напряженность поля выхода E_вых = 3·10⁵ В/см, начальная плотность ионов n₀=10¹⁵ см^-3.

Ρешение. Изменение плотности ионов во времени описывается выражением (3.18). Принимая коэффициент рекомбинации α = 6·10^-6, получим соответственно для t=10 мкс и t=50 мкс:

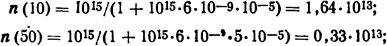
Зная значения плотностей ионов n₀=10¹⁵; n₁₀=1,64·10¹³; n₅₀=0,33·10¹³ см³, можно определить пробивное напряжение для трех моментов времени: 0,1; 10⁵; 5·10⁵ с. Подставляя найденные значения n в уравнение (3.17), выражающее значение пробивного напряжения, получим

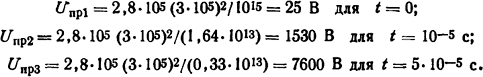
Ответ: U_пр1 = 25 Β; U_пр2=1530 Β; U_пр3=7600 В.

3.4.13. Определить изменение плотности ионов в коротком промежутке во времени, если начальная плотность n₀=2×10¹⁴ см^-3 и коэффициент рекомбинации α=0,5·10^-9.

3.4.14. Определить пробивное напряжение U_пр короткого промежутка через 15 мкс, если плотность ионов n₀=1,5·10¹⁴ см^-3; коэффициент рекомбинации α=10^-9; напряженность поля выхода E_вых = 3,5·10⁵ В/см.

3.5. Отключение цепей переменного тока с длинной дугой

В этом параграфе приведены задачи на гашение дуги переменного тока в длинных промежутках, когда к единичному промежутку приложены сотни, тысячи и десятки тысяч вольт, а также задачи на определение частот восстановления напряжения при различных видах короткого замыкания и разных критических шунтирующих сопротивлениях, последовательно включенных с дугой и индуктивностью в отключаемом контуре. Задачи даны преимущественно для цепей высокого напряжения. При этом используются следующие расчетные формулы и соотношения.

Индуктивность фазы трансформатора при частоте f=50 Гц

где X - процентная реактивность фазы; U - номинальное напряжение, кВ; f - частота тока, Гц, Р_ном - номинальная мощность трансформатора, кВ·А.

Индуктивное сопротивление реактора

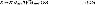
где Х - процентная реактивность реактора; U_ном, I_ном - номинальные напряжения и ток реактора соответственно.

Средняя скорость восстановления напряжения, В/мкс, на первой рвущей фазе выключателя [1]

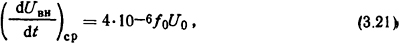
где f₀ - частота колебаний восстановления напряжения на разрыве выключателя; U₀ = 1,5U_ном √2/√3 где U_ном - номинальное напряжение.

Индуктивность трансформатора при высокой частоте восстановления напряжения [4]

3.5.1. Определить ток трехфазного к.з. за трансформатором, у которого номинальная мощность Р_ном=160000 кВ·А, напряжение U_ном = 110 кВ, процентная реактивность X=10%. Пред включенным индуктивным сопротивлением цепи пренебречь.

Решение. Ток к.з. I_кз = I_ном·100/Х. Если умножить числитель и знаменатель этого равенства на √U_ном, то можно выразить значение тока к.з. трансформатора через его номинальные мощность и напряжение:

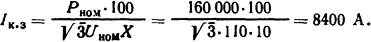
Ответ: I_к.з = 8400 А.

3.5.2. Группа трансформаторов общей мощностью 580000 кΒ·Α, питает шины напряжением U_ном=220 кВ. Определить общее индуктивное сопротивление X и ток к.з., если реактивность трансформатора составляет 8%.

3.5.3. Определить значение индуктивности фазы трансформатора в условиях высокочастотного процесса, если мощность трансформатора Р_ном = 240000 кВ·А; напряжение U_ном=220 кВ; процентная реактивность X=10%, общая емкость фазы трансформатора на землю C=2500 пФ.

Решение. Для промышленной частоты f=50 Гц индуктивность одной фазы трансформатора в соответствии с (3.19)

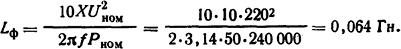
Принимаем эквивалентную емкость на конце обмотки равной половине общей емкости: С_пр=С_ф/2= 2500/2 =1250 пФ.

Частота свободных колебаний без учета снижения индуктивности

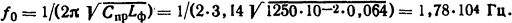
При частоте около 20 кГц индуктивность может снижаться на 20%, т.е. L_f0=0,8·0,064 = 0,051 Гн.

Ответ: L_f0=0,051 Гн.

3.5.4. Определить частоту и среднюю скорость восстановления напряжения на выключателе (первом рвущем полюсе), если имеет место короткое замыкание за выключателем в начале линии, присоединенной к шинам весьма мощной станции или подстанции

через реактор. Номинальное напряжение U_ном=10 кВ, процентная реактивность реактора Х_р = 10%, номинальный ток I_ном = 2000 А. Емкость элементов цепи, находящейся за реактором, определяется следующими составляющими одной фазы: реактор - 200 пФ, трансформатор тока - 1500 пФ, опорные изоляторы - 500 пФ, воздушный выключaтeль - 100 пФ. Частота тока в нормальном режиме f =50 Гц.

Решение. Общая емкость одного полюса на землю С =200+ 150+500+100 = 950 пФ.

Индуктивное сопротивление реактора [см. (3.20)]

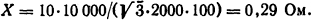
Индуктивность одной фазы реактора

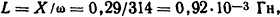
где ω = 2πf=2·3,14·50 = 314 с^-1.

Частота колебания восстанавливающегося напряжения на разрыве выключателя

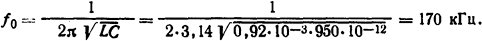
Средняя скорость восстановления напряжения на первой рвущей фазе определится по формуле (3.21)

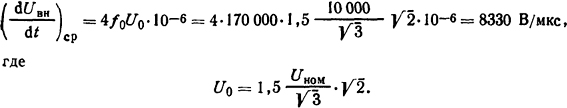
Ответ: f₀ = 170000 Гц, (dU_вн/dt)_ср=8330 В/мкс.

3.5.5. Определить частоту /₀ и скорость восстановления напряжения dU/dt на выключателе, установленном за трансформатором, если Р_ном = 300000 кВ·А. Напряжение U_ном=220 кВ. Емкость одной фазы трансформатора C = 2000 пФ. Нейтраль не заземлена.

3.5.6. Определить частоты и скорости восстановления напряжения в контурах двухчастотного контура для первой рвущей фазы. Напряжение U_ном=110 кВ. Данные первого контура: L₁ = 0,3 Гн, C₁ = 15000 пФ; второго: L₂=0,4 Гн, C₂=2000 пФ.

3.5.7. Определить ток трехфазного к.з. трансформатора и частоту восстановления напряжения на первой рвущей фазе при емкости фазы C = 2000 пФ, если Р_ном = 160000 кВ·А, U_ном = 110 кВ, процентная реактивность X = 8%.

3.5.8. Определить частоту, амплитуду и скорость восстановления напряжения на первом рвущем полюсе выключателя, если короткое замыкание имеет место в начале линии, непосредственно за выключателем, присоединенным к шинам весьма мощной станции через реактор. Данные установки: U_ном=10 кВ; индуктивное

сопротивление реактора X = 80%; I_ном=2000 А; общая емкость одного полюса на землю C = 1000 пФ.

3.5.9. Определить критическую величину шунтирующего сопротивленря на полюсах трехфазного выключателя, которое давало бы при всех возможных режимах к.з. апериодический процесс восстановления напряжения (рис. 3.5, а). Мощность трансформатора

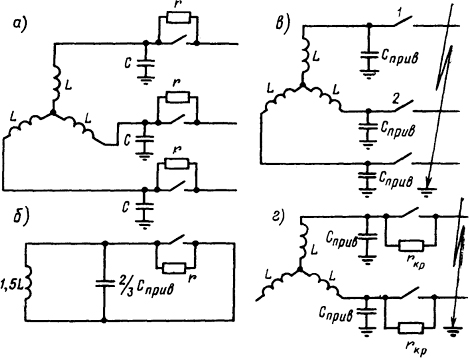
Рис. 3.5. Схема сети и место короткого замыкания

Р_ном=20000 кВ·А. Напряжение U_ном=10 кВ; реактивность Х=6%; емкость обмотки на землю С_тр=1500 пФ. Нейтраль транформатора не заземлена. Емкость оборудования иг шин на землю одной фазы в общей сложности C₀=1000 пФ.

Решение. При частоте 50 Гц индуктивность рассеяния одной фазы трансформатора определим по формуле (3.19)

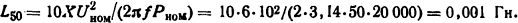
Индуктивность трансформатора при высокой частоте восстановления напряжения будет равна [см. (3.22)]

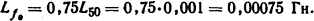
Приведенная расчетная емкость одной фазы трансформатора

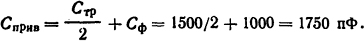
Для различных возможных к.з. за выключателем могут быть приняты следующие приведенные контуры и их параметры:

1. Трехполюсное к.з. без замыкания на землю (рис. 3.5, б). Для первой рвущей фазы без замыкания на землю в месте к.з.

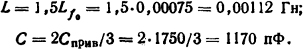
Критическое сопротивление

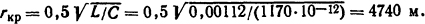
2. Трехполюсное к.з. с замыканием на землю (рис. 3.5, в). Если фаза 1 является первой рвущей, то емкости фаз 2 и 3 оказываются зашунтированными дуговым замыканием на землю. В приведенном контуре в этом случае будет индуктивность L=1,5L_f0= 0,00112 Гн, как в предыдущем случае. Емкость в приведенном контуре будет равна фазовой приведенной емкости С_прив, а критическое сопротивление

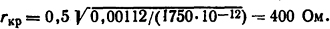
3. Двухполюсное к.з. (без земли) (рис. 3.5, г) :

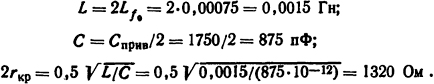
В данном случае присутствуют два сопротивления на полюсах и, следовательно, сопротивление на один полюс r_кр= 1320/2 =660 Ом. Таким образом, наименьшее из значений критических сопротивлений дает случай трехфазного к.з. с замыканием на землю (r_кр=400 Ом). Выбираем шунтирующее сопротивление с двойным запасом, а именно: r_ш=r_кр/2= 400/2 = 200 Ом. Такое сопротивление обеспечит апериодический процесс восстановления напряжения в довольно широких пределах изменения постоянных контура.

Ответ: r_ш=200 Ом.

3.5.10. Определить значение критического сопротивления Гкр, шунтирующего фазу выключателя при мощности P_ном = 5000 кΒ·Α. Приведенная к фазе выключателя емкость С_прив =2500 пФ, номинальное напряжение U_ном=20 кВ.

3.6. Отключение малых емкостных и индуктивных токов

В этом параграфе рассмотрены задачи на отключение токов трансформаторов и воздушных линий передачи переменного тока, на определение превышения напряжения на выключателе в случае отключения зарядного тока линии при различных значениях шунтирующего сопротивления и значения первой наибольшей амплитуды напряжения при отключении холостых трансформаторов в условиях среза токов, а также на определение условий отключения одной фазы линии передачи и значений сопротивлений, шунтирующих выключатель для ограничения напряжения на определенном уровне. При этом используются следующие расчетные формулы и соотношения.

Наибольший пик напряжения при срезе тока на максимуме

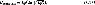
где I₀ - ток холостого хода трансформатора, A; L₀ - индуктивность одной фазы трансформатора; Гн; С - приведенная емкость, Ф.

Остаточный ток при однофазном отключении

где U - напряжение сети, Α; ω=2πf; f - частота тока, Гц; С - междуфазовая емкость, Ф; l - длина линии передачи, м.

Коэффициент превышения напряжения на выключателе при отключении емкостного тока [1]

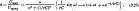
где ω - угловая частота сети; r - шунтирующее сопротивление на фазу, Ом; С - отключаемая фазовая емкость, Ф.

Значение напряжения, кВ, остаточного дугового столба открытой дуги

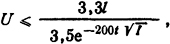
где l - длина дуги, м; t - время, с; I - ток, А.

3.6.1. Определить начальную скорость и амплитуду восстановления напряжения на выключателе при отключении холостой линии емкостью C от трансформатора, если номинальная мощность трансформатора Р_ном=5000 кВ·А, номинальное напряжение U_ном=110 кВ, процентная реактивность Х=12%, приведенная емкость C=0,l мкФ. Зарядный ток холостой линии I=25 А частоты f=50 Гц.

Решение. Индуктивность фазы трансформатора в соответствии с (3.19)

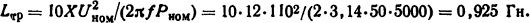
Амплитуда падения напряжения на сопротивлении рассеяния трансформатора

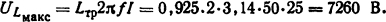
Собственная частота колебаний напряжения

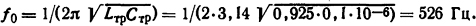
Начальная средняя скорость восстановления напряжения на выключателе определится из формулы (3.21)

Ответ: U_Lмакс = 7,26 кВ; (dU_в/dt)_ср=15,2 В/мкс.

3.6.2. Определить значение тока х.х. линии длиной l=100 км при номинальном напряжении U_ном = 220 кВ, если ее отключают от бесконечно мощного источника энергии. Найти перенапряжение на линии, если при отключении имеет место образование двух повторных пробоев на амплитудном напряжении.