Простейшие методы расчета нагрева я охлаждения электрических аппаратов и их частей 10 страница

3.6.3. Трехфазный трансформатор работает то в режиме к.з., то в режиме отключения х.х. Определить частоты восстановления и амплитуды напряжений, если мощность трансформатора Р_ном=120 MB·А; напряжение U_ном=110 кВ; реактивность к.з. X=10%; ток х.х. I₀ = 2%; приведенная емкость С = 2000 пФ; f = 50 Гц.

Решение. Индуктивность рассеяния одной фазы трансформатора можно определить по формуле (3.19).

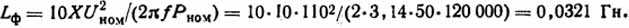
Частота колебания восстанавливающегося напряжения в режиме к.з.

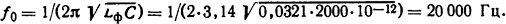
Амплитуда первого пика восстанавливающегося напряжения [1]

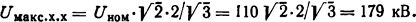
Ток х.х. трансформатора

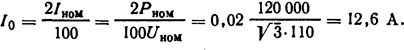
Индуктивное сопротивление фазы обмотки трансформатора в режиме х.х.

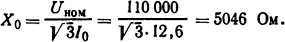
Тогда индуктивность одной фазы L₀=X₀/ω= 5046/314 =16,1 Гн.

Частота колебания напряжения на трансформаторе в режиме х.х.

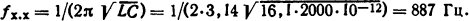
Наибольший пик напряжения при срезе тока на максимуме

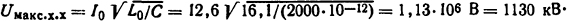
Ответ: f₀=20000 Гц; f_x.x = 887 Гц; U_{макс к.з}=179 кВ; U_{макс х.х} = 1130 кВ.

3.6.4. Определить значение шунтирующего сопротивления полюса выключателя для ограничения (до 215 кВ) перенапряжения х.х. трансформатора, если его мощность Р_ном = 120000 кВ·А, напряжение U_ном=110 кВ, суммарная емкость, приведенная к началу фазы (вводу), С_прив = 3500 пФ, процентная реактивность Х = 10%.

3.6.5. Определить пик ожидаемого напряжения на трансформаторе при отключении х.х. если мощность одного полюса трансформатора Р_ном = 60000 MB·А, напряжение U_ном = 70 кВ. Ток х.х. составляет 3% от номинального, емкость фазы трансформатора C=2000 пФ, емкость остальных элементов (шин, изоляторов, трансформатора тока) выключателя C=1800 пФ.

3.6.6. На линии электропередачи напряжением U = 220 кВ и протяженностью t = 60 км произошло однофазное короткое замыкание на землю, которое можно устранить с помощью одного полюса выключателя. Оценить возможность деионизации остаточного столба дуги, если междуфазовая емкость C = 0,001 мкФ/км, частота сети f = 50 Гц.

Решение. При однофазном отключении остаточный дуговой столб будет получать подпитку от междуфазовых емкостных связей. Ток подпитки определим из формулы (3.24) :

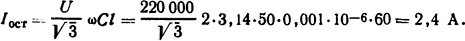
При емкостных связях и полной деионизации остаточного столба дуги возвращающееся напряжение на отключенном проводе по отношению к земле

U_з≈0,15·U/√3 = 0,15·220000/√3= 19100 Β = 19,1 κΒ. Критическая длина дуги за счет подпитывающего тока

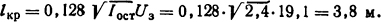
На основании экспериментальных данных действительная длина дуги за счет мелких петель и изгибов получается по крайней мере в 2 раза больше, чем расчетная, поэтому для угасания дуги ее кажущаяся длина должна быть l<l_кр/2 = 3,8/2 =1,9 м.

При номинальном напряжении 220 кВ наименьшее расстояние по гирлянде изоляторов П-4,5 составляет 2,5 м, однако следует иметь в виду, что при протекании тока к.з. через дуговой столб он будет растянут электродинамическими силами, создаваемыми током к.з. Таким образом, несомненно, путь остаточного тока будет значительно больше, чем кажущаяся длина дуги, и, следовательно, дуга остаточного тока гореть не сможет и должна угаснуть.

Ответ: остаточная дуга угасает.

3.6.7. Оценить возможность гашения дуги на линии, возникающей при перекрытии фаза - земля при условии пофазного отключения. Напряжение U_ном=110 кΒ, длина линии t=50 км.

3.6.8. Определить условие самоугасания открытой дуги, если начальный ток дуги I=100 А, линейное напряжение сети U_ном = 110 кВ. Дуга возникает между проводом и землей.

3.6.9. Определить максимальный ток, который можно разомкнуть с помощью открытой дуги, если длина, на которую может быть растянута дуга в процессе отключения, l_д=8 м, а номинальное напряжение U_ном = 6 кВ.

3.6.10. Оценить кратность напряжения, возникающего на выключателе при отключении им участка линии емкостью C=1,5 мкФ, если каждая фаза выключателя зашунтирована сопротивлением r=3000 Ом. Повторные пробои и замыкания не принимаются во внимание.

Решение. Повышение напряжения на выключателе при отключении им емкостного тока [4] определим на основе формулы (3.25)

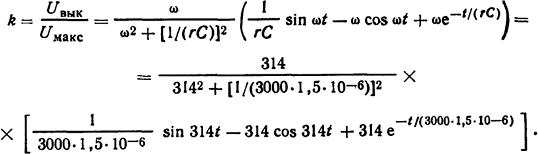
Наибольшая кратность напряжения, как показано в [4], наступает при t = 0,0076 с и составляет k = 0,92.

Ответ: k = 0,92.

3.6.11. Оценить ориентировочное значение напряжения остаточного дугового столба через время t = 0,3 с после его отключения, если до отключения ток дуги I=1000 А. Дуга открытая, длина канала достигает l = 2,0 м.

Решение. Оценить это напряжение можно с помощью формулы (3.26):

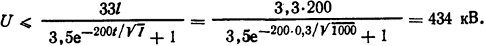
Ответ: U=434 кВ.

3.6.12. Оценить сопротивление остаточного дугового канала, если номинальное напряжение цепи U_ном=110 В, а остаточный ток I=200 мА.

4.2. Сваривание контактов

В этом параграфе даны задачи на сваривание контактов аппаратов. Сваривание контактов - весьма сложное явление сочетания тепловых и динамических процессов. При расчете токов сваривания используются следующие расчетные формулы и соотношения

Минимальный сваривающий ток [1]

где m=1,5... 2 - коэффициент, α - радиус площадки касания, м; λ - коэффициент теплопроводности материала контактов, Вт/(м·К); ϑ_пл - температура плавления материала контактов, °С; ρ - удельное сопротивление материала контактов, Ом·м.

Эмпирическая формула Буткевича для определения минимального тока сваривания [4]

где k - коэффициент, зависящий от материала и типа контактов; Ρ - усилие контактного нажатия.

4.2.1. Два стержня диаметром d=20 мм сжаты силой Р=390 Н. Торцы обработаны таким образом, что образуют сферические поверхности радиуса r= 10 мм. Определить, какой постоянный ток в течение времени t=0,2 с эти контакты могут выдержать без сваривания.

Решение. Минимальный сваривающий ток определяется по формуле (4.10)

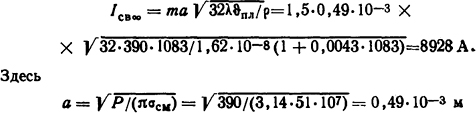
- радиус площадки касания; m=1,5 - коэффициент; σ_см=51·10⁷ Н/м² - напряжение смятия для меди (см. табл. П.16); λ=390 Вт/(м·К) -теплопроводность меди; ϑ_пл = 1083°С- температура плавления меди, ρ=1,62·10^-8 Ом·м - удельное сопротивление меди при 0°С. Для параметра

4.2.2. Определить ток сваривания в задаче 4.2.1, если сила контактного нажатия Р=1000 Н, а все остальные данные остались без изменения.

4.2.3. Определить сваривающий ток медных контактов, образуемых параллельными стержнями и перемычкой (траверсой).

Контакты торцовые, диаметр стержня d=20 мм. Расстояние между осями стержней а=400 мм. Механическая сила, сжимающая контакты (каждую пару), Ρ=200 Η, контакты одноточечные.

4.2.4. Определить минимальный сваривающий ток розеточного контакта из меди, если сила нажатия на одну ламель составляет 50 Н, всего ламелей 6 шт.

Решение. Величина амплитуды минимального сваривающего тока может быть определена по формуле (4.4) для случаев, когда наибольший пик симметричного тока получается в начале процесса:

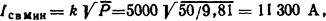
где Ρ - сила сжатия контактов, k = 5000 - числовой коэффициент для одной ламели.

Для шести ламелей сваривающий ток можно получить по крайней мере в 6 раз большим:

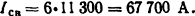
В действительности сваривающий ток может оказаться более высоким, если учитывать силу взаимодействия между ламелями.

Ответ: I_св=67,7 кА.

4.2.5. Определить минимальный ток сваривания медных контактов, сжимаемых с силой Р=150 Н, если ток при к.з. имеет сильное затухание симметричной составляющей (т.е. возможно сваривание только на первом максимальном пике).

4.2.6. Определить минимальный сваривающий ток для сильно затухающего симметричного тока в пальцевых медных контактах, сжимаемых силой Ρ = 100 Н, для несамоустанавливающихся и самоустанавливающихся пальцев и сравнить полученные результаты.

4.2.7. Определить допустимую величину амплитуды тока к.з. для розеточного контакта выключателя, если величина контактного нажатия, которое осуществляется каждой ламелью розетки, Р= 100 Н, число ламелей в контакте n=6.

4.2.8. Определить требуемую с точки зрения сваривания величину контактного нажатия медного щеточного контакта пускового реостата, если максимальное значение амплитуды ударного тока к.з. i_уд =10 кА.

4.2.9. Определить минимальный ток сваривания самоустанавливающегося пальцевого медного контакта, прижимаемого пружиной с силой 100 Н. Допускаем, что составляющая симметричного тока имеет сильно затухающий характер. Сваривание в этом случае возможно только на первой наибольшей полуволне тока.

4.2.10. Определить силу, с которой должны сжиматься между собой медные контакты, если амплитуда наибольшего тока в цепи может достигнуть I_макс=30 кА. Результаты сравнить, когда контакты снабжены медно-вольфрамовыми накладками.

4.2.11. Оценить предельный минимальный сваривающий ток контакта разъединителя с учетом механической силы, сжимающей

контакты и внешних электродинамических сил, возникающих от взаимодействия шин длиной l=0,5 м. Максимальный ток, протекающий через каждый контакт, I=20 кА. Расстояние между осями шин а=0,04 м. Механическая сила, сжимающая контакты, постоянна; Р=100 Н.

Решение. Электродинамическая сила, прижимающая один контакт, Ρ/2=10^-7I²2l/(2a) = 10^-7(20000)²2·0,5/(0,04·2)=500 Η. Общая сила на один контакт Р_Σ =500+100=600 Н. Амплитуда сваривающего тока для одного контакта по формуле (4.11) будет равна

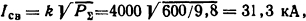
где k = 4000 - числовой коэффициент [4].

Этот ток больше действительного тока, приходящегося на один контакт (20 кА), и, следовательно, сваривания не произойдет.

Ответ: I_св=31,3 кА.

4.2.12. Определить минимальный сваривающий ток к.з. одноточечного латунного контакта разъединителя, сжимаемого с силой Р=150 Н, если подводящие шины дополнительно сжимают контакты с максимальной электродинамической силой, развиваемой током. Размеры шин 5×30 мм, расстояние между шинами а=10 мм, а длина их l=0,5 м.

ГЛАВА 5. РАСЧЕТ ЭЛЕКТРОМАГНИТНЫХ МЕХАНИЗМОВ

5.1. Расчет магнитных проводимостей воздушных промежутков

В данном параграфе рассматриваются задачи по расчету магнитных проводимостей путей магнитного потока по воздуху, характерных для электромагнитных механизмов постоянного и переменного тока. Приводятся задачи

по расчету преводимостей рабочих и паразитных зазоров, проводимостей рассеяния и суммарных проводимостей различных магнитных систем (клапанного, броневого и других типов), а также цепей с постоянными магнитами, применяющихся в поляризованных и других системах электрических аппаратов. В дальнейшем тексте теории и задач пятой главы¹ будем для упрощения использовать термин электромагнит, подразумевая электромагнитный механизм, т.е. такое устройство, в котором электрическая энергия преобразуется в механическую (приводы высоковольтных выключателей, магнитные пускатели, контакторы, реле, силовые электромагниты и т.п.).

При равномерном (однородном) поле магнитная проводимость воздушного промежутка (Гн)

где μ₀=4π·10^-7 Гн/м - магнитная постоянная; S - площадь полюса, м²; δ - величина воздушного промежутка, м.

Для цилиндрических с диаметром d или квадратных со стороной α полюсов, обращенных друг к другу торцовыми поверхностями, поле можно считать равномерным при d/δ, а/δ≥20 (приближенно при d/δ, а/δ≥10 [6]); поле также можно считать равномерным для паразитных зазоров.

Магнитное сопротивление (являющееся величиной, обратной проводимости) (Гн^-1) равно

где μ₀=4π·10^-7 Гн/м; S - площадь полюса, м²; δ - воздушный зазор, м.

При неравномерном поле расчет магнитных проводимостей поля с боковой поверхности полюсов вблизи воздушного зазора может быть произведен по кривым Буля [1], приведенным на рис. П.17 и П.20 приложения.

Расчет магнитных проводимостей с учетом выпучивания может быть сделан также по формулам Сливинской, полученным путем математической обработки экспериментальных данных, на основании разработанного метода подобия магнитных полюсов [14].

Для обращенных друг к другу цилиндрических полюсов диаметром d (м) упрощенная формула проводимости с учетом выпучивания с торца

где μ₀=4π·10^-7 Гн/м; δ - зазор, м.

Формулы для расчета проводимостей квадратных, конических и цилиндрических полюсов приведены в табл. П.25.

Для броневого электромагнита с внутренним диаметром кожуха D проводимость рабочего зазора б с учетом поля выпучивания с торцов и боковой поверхности цилиндрических полюсов диаметром d определяют по формуле [6]

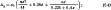
здесь μ₀=4π·10^-7 Гн/м; x=(D-d)/π-δ/2 (считается, что линии потока выпучивания замыкаются по дугам полуокружностей) ; D, d, δ - в м.

Для рабочего зазора клапанного электромагнита с цилиндрическим полюсом, имеющим полюсный наконечник (шляпку), проводимость с учетом

выпучивания с торца и с боковой поверхности шляпки находят по формуле [14]

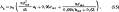
где μ₀=4π·10^-7 Гн/м; δ, d_шл и h_шл - соответственно зазор, диаметр и толщина шляпки, м; ϰ₁ - коэффициент, равный

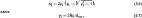
где R₀ - расстояние от оси вращения якоря до оси полюса, м.

Для концентрических полюсов, имеющих постоянный зазор δ, толщину а, ширину b и радиус r (м), проводимость (Гн) без учета выпучивания находят, по формуле

здесь μ₀=4π·10^-7 Гн/м; β - угол перекрытия, рад, равный

где α - угол сдвига между осью полюсов и осью якоря.

Удельная магнитная проводимость (на единицу длины в осевом направлении) (Гн/м) для параллельных цилиндров с радиусами r₁, r₂, оси которых находятся на расстоянии h (м), равна

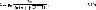
где μ₀=4π·10^-7 Гн/м; u - коэффициент, равный

Формулы для расчета удельной проводимости между параллельными цилиндрами для других случаев приведены в табл. П.23 (по этим формулам определяют обычно удельную проводимость рассеяния λ_σ).

По методу вероятных путей потока Ротерса суммарная магнитная проводимость между двумя параллельными призмами равна

где Λ_элi - проводимость элементарного t'-ro пути магнитного потока.

Для проводимости между двумя параллельными гранями шириной с и длиной b, лежащими в одной плоскости на расстоянии δ (элементарная геометрическая фигура-полукольцо), при δ<3с имеем

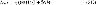
где μ₀=4π·10^-7 Гн/м; размеры b, с и зазор δ выражаются в метрах.

Формула для определения проводимости при δ≥3с, а также формулы для проводимостей между остальными элементами параллельных призм приведены в табл. П.28. При вычислении проводимости между призмой и плоскостью следует учесть, что путями магнитного потока будут полуобъемы от показанных в табл. П.28. Тогда проводимость каждого элементарного пути будет вдвое больше соответствующей проводимости, указанной в

табл. П.28 [или в формуле (5.10)]; при этом за длину воздушного зазора принимают удвоенное расстояние от плоскости до торца призмы.

Расчет магнитных проводимостей с торца коаксиального цилиндра на кожух (например, для электромагнитов с незамкнутой магнитной цепью) может быть произведен по формулам² табл. П.29.

Для параллельных граней призмы (с размерами a, b и шириной с), находящихся на расстоянии δ и обращенных в противоположные стороны, расчет ведут по формуле Кремпа и Кольдервуд, полученной методом конформных преобразований:

Здесь μ₀=4π·10^-7 Гн/м; λ' находят по n'=a/δ, λ" - по n"=b/δ (в зависимости от коэффициента m=(δ+2с)/δ) с помощью рис. П.18.

При плоскопараллельном поле проводимость с учетом выпучивания может быть найдена по построенной графическим путем картине поля. Для этого проводят эквипотенциальные линии и линии индукции, выходящие с поверхности полюса под прямым углом (считая, что полюса не насыщены и их поверхности эквипотенциальны), добиваясь при этом перпендикулярности пересечений вышеуказанных линий, а также равенства средних размеров криволинейных квадратов, заключенных между ними. Используя полученную картину поля, проводимость между полюсами находят по формуле

где μ₀=4π·10^-7 Гн/м; m_i - число трубок магнитного потока; n_i - число элементов в каждой трубке; h - толщина поля, м. Суммарная магнитная проводимость двух зазоров δ₁ и δ₂, через которые последовательно проходит магнитный поток, равна

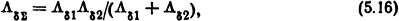
где Λ_δ1 и Λ_δ2 - соответственно проводимости зазоров δ₁ и δ₂, Гн.

Для двух одинаковых зазоров

5.1.1. Определить суммарную проводимость рабочих зазоров полюсов, показанных на рис. 5.1, без учета выпучивания. Размеры полюсов: b=2·10^-2 м, r=2·10^-2 м, толщина полюса (в направлении, перпендикулярном чертежу) a=2·10^-2 м; δ=0,06·10^-2 м; угол α=15°.

Решение. Определив по (5.9) угол перекрытия β=2 arcsin (2·10^-2/2·2·10^-2)-15=45°= 0,785 рад находим согласно (5.8) проводимость одного зазора

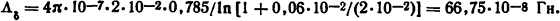
Суммарная проводимость по (5.16а) Λ_δΣ = Λ_δ/2 = 66,75·10^-8/2≈33,4·10^-8 Гн.

Ответ: Λ_δΣ =33,4·10^-8 Гн.

5.1.2. Решить предыдущую задачу при α=0°.

Ответ: Λ_δΣ=44,5·10^-8 Гн.

5.1.3. Определить суммарную проводимость рабочих зазоров и удельную проводимость рассеяния прямоходового электромагнита,

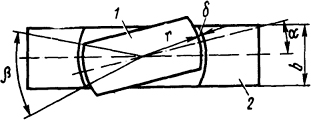
Рис. 5.1. Концентрические полюса: 1 - якорь; 2 - полюсные наконечники

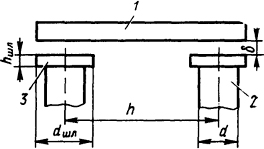
Рис. 5.2. Полюса прямоходового электромагнита с внешним притягивающимся якорем: 1 - якорь; 2 - сердечник; 3 - полюсный наконечник (шляпка)

полюса которого показаны на рис. 5.2, для δ=0,1·10^-2м, если d_шл=2,4·10^-2 м; h_шл=0,3·10^-2 м; h=3,6·10^-2 м; d=1,6·10^-2 м.

Решение. Применив формулу (5.4) для полюсов подковообразного электромагнита и подставив в нее d=d_шл и х=h_шл, найдем

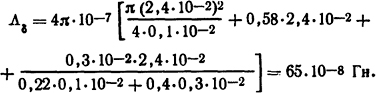
Согласно формуле (5.16а) суммарная проводимость Λ_δΣ = 65·10^-8/2 = 32,5·10^-8 Гн. Удельную проводимость рассеяния определяем по формуле (1) табл. П.23 (n=h/d=3,6·10^-2/1,6·10^-2 = 2,25):

Ответ: Λ_δΣ = 32,5·10^-8 Гн; λ_σ = 2,7·10^-8 Гн/м.

5.1.4. Для клапанного электромагнита, имеющего полюсный наконечник (шляпку), рассчитать по формуле (5.5) проводимость рабочего зазора. Найти предварительно по формуле (5.7) значение коэффициента ρ₁, зависящего ог соотношения размеров, а по формуле (5.6) - соответствующее ему значение ϰ₁. Рабочий зазор δ=0,5·10^-2 м. Размеры (рис. 5.3): d=1·10^-2 м; h_шл=0,3·10^-2 м; d_шл=1,5·10^-2 м; h=1,5·10^-2 м; a_яр=0,5·10^-2 м, необходимый для вычисления ρ₁ размер R₀=h+a_яр+0,5d.

Ответ: τ₁ = 3,33; ϰ₁ = 1,024; Λ_δ=9,7·10^-8 Гн.

5.1.5. Для условий предыдущей задачи определить суммарную проводимость воздушных зазоров и удельную проводимость рассеяния магнитной системы при b_яр=1,6·10^-2 м.

Решение. Полюса магнитной системы, показанные на рис. 5.3, имеют два изменяющихся зазора δ и δ_е. По заданному значению δ, используя соотношение 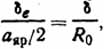, находим соответствующее значение

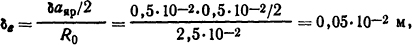
где R₀ =h-а_яр+0,5d =1,5·10^-2+0,5·10^-2 +0,5·1·10^-2= 2,5·10^-2 м. Проводимость паразитного зазора δ_е определяем по (5.1):

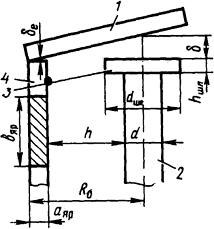
Рис. 5.3. К определению проводимости между тор-дом цилиндра и наклонной плоскостью: 1 - якорь; 2 - сердечник; 3 - полюсный наконечник; 4 - ярмо

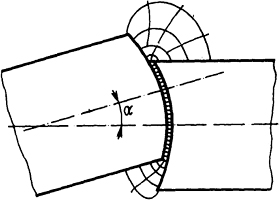
Рис. 5.4. Картина поля в зазоре концентрических полюсов

Суммарная проводимость согласно (5.16)

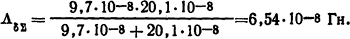
Проводимость рассеяния определяем по формуле (2) табл. П.23. С учетом отношения b_яр/h=1,6·10^-2/(1,5·10^-2) = 1,07<1,25, принимаем k_a=0,8; тогда

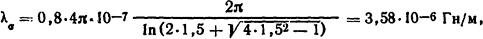
5.1.6. Решить задачи 5.1.4 и 5.1.5 при δ=2,5·10^-3 м и h=2·10^-2 м.

5.1.7. Используя метод графического построения картины поля, определить проводимость рабочих зазоров электромагнита с внешним поперечно-движущимся якорем по данным, приведенным

в задаче 5.1.1, с учетом полей выпучивания. Сопоставить результат с ответом задачи 5.1.1.

Решение. По заданным размерам с учетом масштаба вычерчиваем эскиз полюсов (рис. 5.4) и, выполняя указанные в теории рекомендации, проводим линии потока и эквипотенциальные линии. Исходя из рис. 5.4 m₁=26 (число трубок с одним элементом), m₂=6 (число трубок с двумя элементами) и m₃=2 (число трубок с четырьмя элементами). Учитывая, что h=a=2·10^-2 м, находим по формуле (5.15): Λ_δ=4π·10^-7·2·10^-2(26/1+6/2+2/4) =74,13·10^-8 Гн. Суммарная проводимость рабочих зазоров согласно (5.16а) Λ_δΣ = Λ_δ/2 = 74,13·10^-8/2≈37,07·10^-8 Гн. Таким образом, с учетом выпучивания проводимость получается на 11% больше, чем без учета выпучивания (Λ_δΣ =33,4·10^-8 Гн найдено в задаче 5.1.1).

Ответ: Λ_δΣ = 37,07·10^-8 Гн, что на 11% больше значения проводимости без учета выпучивания (полученного в задаче 5.1.1).

5.1.8. Решить задачу 5.1.7 при α=20°, 10°, 5°.

5.1.9. Для магнитной системы с втягивающимся якорем (рис. 5.5), имеющим плоский торец, определить проводимость рабочего зазора δ с учетом поля выпучивания (Λ_δ) и без учета поля выпучивания (Λ_δ') при δ=0,4·10^-2 м, а также удельную проводимость

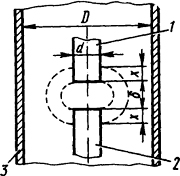
Рис. 5.5. К определению проводимости с учетом выпучивания с боковых поверхностей цилиндрических полюсов: 1 - якорь; 2 - стоп; 3 - корпус

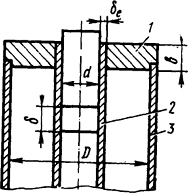
Рис. 5.6. Эскиз к определению проводимости паразитного зазора δ_е: 1 - верхний фланец; 2 - немагнитная направляющая втулка; 3 - корпус

рассеяния λ_σ. Найдя при заданных размерах отношение d/δ, выяснить, какой процент составляет проводимость выпучивания от величины полной проводимости. Размеры: D=8·10^-2 м; d=3,3·10^-2 м.

Решение. Без учета выпучивания согласно (5.1) Λ_δ'=4π·10^-7·π(3,3·10^-2)²/(4·0,4·10^-2) =26,9·10^-8 Гн. С учетом поля выпучивания с торцовой и боковой поверхности согласно (5.4)