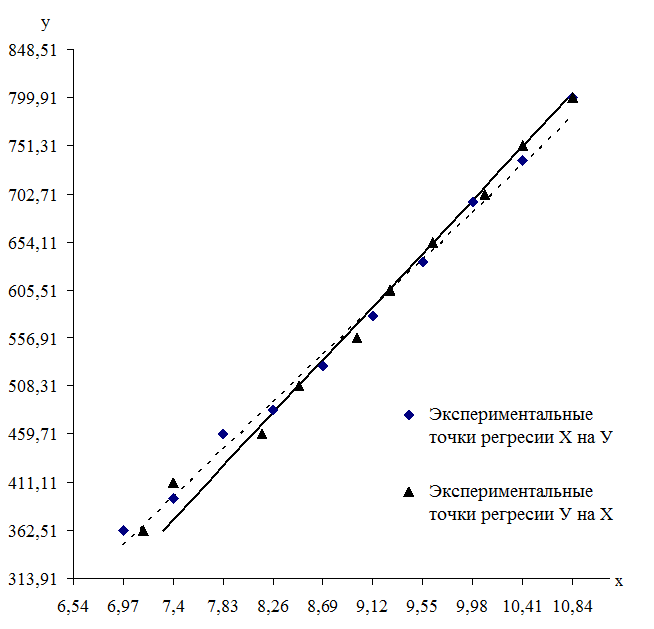
Построение линейной регрессионной модели

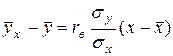и

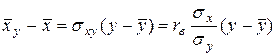
По формуле (5) определим выборочный коэффициент корреляции, для чего сначала вычислим

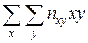= 534309,8911.

r_в= 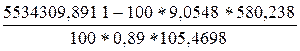=0,9458.

Так как полученный коэффициент 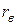равен 0,9458, то линейная связь между признакам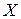и и 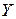весьма высокая.

Найдем выборочные коэффициенты регрессии:

r_yx=r_в 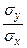=0,9458 105,4698/0,89=111,6114;

r_xy=r_в 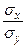=0,9458·0,89/105,4698=0,008.

Следовательно, выборочное уравнение прямой линии регрессии 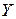на 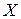(6) имеет вид

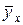–580,238=111,611 (x–9,0548); 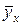=111,611 x–430,3773.

Выборочное уравнение прямой линии регрессии 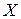на 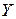(7) имеет вид

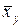–9,0548=0.008(y–580,238); 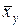=0.008 y+4,412896.

Точкой пересечения двух прямых является точка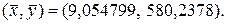

	Рисунок 1 – Прямые линии регрессии 1: =111,611 x–430,3773. 2: =0,008 y+4,412896.

Точечная и интервальная оценки коэффициента корреляции генеральной совкупности

Точечная оценка: , ;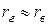

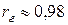Интервальная оценка (8):

0,9458– 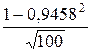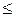r_г£0,9458+ ;

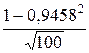0,9142£r_г£0,977449.

Проверка гипотезы о значимости выборочного коэффициента корреляции

Проверим нулевую гипотезу о равенстве нулю генерального коэффициента корреляции 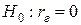при конкурирующей гипотезе .

.

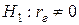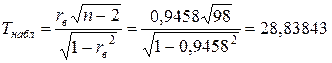Найдем 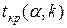, где 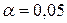– уровень значимости, 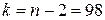– число степеней свободы; 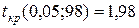. Сравним 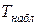и 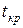: 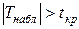– нулевую гипотезу отвергаем, выборочный коэффициент значимо отличается от нуля, т.е. 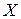и 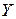линейно коррелированы.