Порядок проверки адекватности модели

1. Определяют сумму квадратов, характеризующую адекватность модели 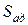. При равномерном дублировании опытов

,

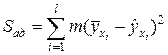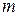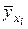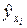где – число дублированных опытов в каждой серии, – среднее значение результатов в -той серии дублированных результатов, – теоретическое значение, вычисленное с помощью полученной регрессионной модели.

В случае неравномерного дублирования

,

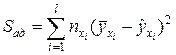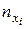– число дублированных опытов в -той серии.

2. Вычисляют число степеней свободы 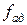дисперсии адекватности. При любой методике дублировании .

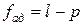3.Вычисляют дисперсию адекватности

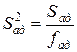(19)

С помощью 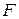-критерия Фишера проверяют однородность дисперсии адекватности (18) и дисперсии воспроизводимости (19). При этом вычисляют

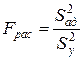, (20)

которое сравнивается с табличным значением 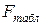, найденным при выбранном уровне значимости a для чисел степеней свободы 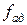, в числителе и 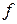в знаменателе ( ).

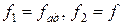Если 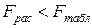, то модель считается адекватной и может быть использована для описания объекта. В противном случае модель не адекватна.

Рассмотренный метод проверки адекватности играет простой физический смысл.

В основе этой процедуры лежит проверка гипотезы об однородности дисперсии адекватности и дисперсии, характеризующей ошибку эксперимента. Заметим, что дисперсия адекватности характеризует расхождение между результатами эксперимента 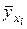и значениями выходной величины 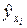, вычисленными по уравнению регрессии. Очевидно, что модель удовлетворительно описывает объект исследования, т.е. является адекватной, если указанное расхождение вызвано только экспериментальными ошибками, а не связано, например, с неудачным выбором вида математической модели.

Проверка гипотезы об однородности рассматриваемых дисперсий и выясняет общность происхождения экспериментальных ошибок и расхождения между 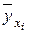и .