Вычисление корреляционных отношений
Вычислим по формуле (14) корреляционное отношение 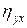 .
.
 1066412,721/100=10664,12721;
1066412,721/100=10664,12721;
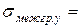
 =103,2673;
=103,2673;
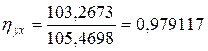 .
.
Аналогично находим 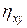 по формуле (15).
по формуле (15).
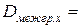 1/100*77,47869723=0,774787;
1/100*77,47869723=0,774787;  ;
;
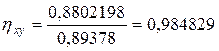 .
.
Следовательно, 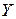 связан с
связан с 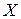 корреляционной зависимостью.
корреляционной зависимостью.
Построение квадратичной регрессионной модели по методу наименьших квадратов
Предположим, что СВ 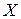 и
и 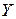 связаны следующим уравнением
связаны следующим уравнением 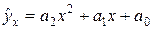 . Система линейных уравнений для нахождения оценок коэффициентов аппроксимирующего многочлена
. Система линейных уравнений для нахождения оценок коэффициентов аппроксимирующего многочлена  , полученная методом наименьших квадратов, имеет вид:
, полученная методом наименьших квадратов, имеет вид:
 (22)
(22)
Найденные из этой системы выборочные параметры 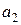 ,
, 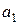 ,
, 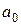 подставляют в выборочное уравнение регрессии
подставляют в выборочное уравнение регрессии 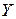 на
на 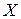 :
: 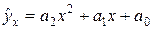 и в итоге получают искомое уравнение регрессии.
и в итоге получают искомое уравнение регрессии.
Составим расчетную таблицу
| № | 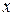
| 
| 
| 
| 
| 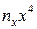
| 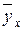
| 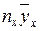
| 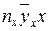
| 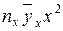
|
| 6,97 | 20,895 | 145,5337 | 1013,642046 | 7060,016853 | 362,51 | 1087,53 | 7574,64645 | 52757,41252 | ||
| 7,40 | 44,37 | 328,1162 | 2426,418929 | 17943,36798 | 394,91 | 2369,46 | 17522,1567 | 129576,3488 | ||
| 7,83 | 15,65 | 122,4613 | 958,2592813 | 7498,378876 | 459,71 | 919,42 | 7194,4615 | 56296,66124 | ||
| 8,26 | 115,57 | 954,0304 | 7875,520539 | 65012,42205 | 484,01 | 6776,14 | 55937,0357 | 461760,2297 | ||
| 8,69 | 121,59 | 1056,009 | 9171,439468 | 79653,95178 | 529,14 | 7407,96 | 64338,1326 | 558776,6816 | ||
| 9,12 | 218,76 | 1993,997 | 18175,2863 | 165667,7346 | 579,185 | 13900,44 | 126702,511 | 1154893,384 | ||
| 9,55 | 133,63 | 1275,498 | 12174,63175 | 116206,8601 | 633,28 | 8865,92 | 84625,2064 | 807747,5951 | ||
| 9,98 | 109,725 | 1094,507 | 10917,70608 | 108904,1181 | 693,87 | 7632,57 | 76134,8858 | 759445,4854 | ||
| 10,41 | 104,05 | 1082,64 | 11264,8718 | 117210,9911 | 736,73 | 7367,3 | 76656,7565 | 797613,5514 | ||
| 10,84 | 21,67 | 234,7945 | 2543,997866 | 27564,21688 | 799,91 | 1599,82 | 17334,0497 | 187814,4285 | ||
| ∑ | 89,00 | 100,00 | 905,91 | 8287,59 | 76521,77 | 712722,06 | 5673,26 | 57926,56 | 534019,84 | 4966681,78 |
Получим систему уравнений:
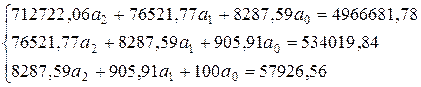
Решим полученную систему:
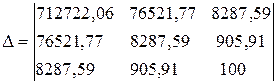 =855819,84;
=855819,84;
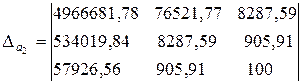 =5564530,01;
=5564530,01;
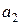 =
=  =5564530,01/855819,84=6,502;
=5564530,01/855819,84=6,502;
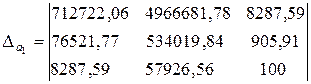 =–1368934,16;
=–1368934,16;
 =
=  =–1368934,16/855819,84=–1,5996;
=–1368934,16/855819,84=–1,5996;
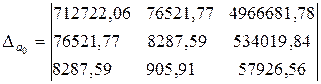 =46982871,1;
=46982871,1;
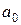 =
=  =46982871,1/855819,84=54,898.
=46982871,1/855819,84=54,898.
Получаем выборочное уравнение регрессии 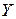 на
на 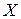 :
:
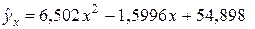 .
.
|

Точечные оценки параметров уравнения регрессии 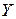 на
на 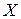 генеральной совокупности.
генеральной совокупности.
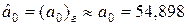 ;
;  ;
; 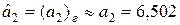 .
.
Дата добавления: 2016-02-24; просмотров: 567;
