Пример выполнения расчетно-графической работы
Данные для статистической обработки
| Столбец 1 | Столбец 2 | Столбец 3 | Столбец 4 | Столбец 5 | |||||

| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| 8,91 7,36 9,10 9,80 8,43 10,10 7,45 9,01 8,07 8,86 | 560,47 395,40 583,13 668,37 506,74 706,87 404,02 571,92 467,60 554,50 | 10,19 10,71 9,68 9,33 8,93 9,03 10,11 7,46 9,30 8,62 | 718,20 788,63 653,88 610,69 562,38 574,46 708,69 405,15 606,14 526,98 | 8,92 7,33 8,63 9,24 8,66 8,44 9,54 8,02 8,62 8,12 | 561,67 392,71 528,04 599,47 532,26 507,66 636,39 462,43 527,94 472,49 | 9,73 8,43 7,95 9,89 9,93 8,49 6,75 8,38 8,72 9,57 | 659,48 506,18 454,53 680,49 684,68 512,47 338,21 501,19 539,20 639,34 | 9,96 9,42 9,24 9,56 8,29 7,13 9,42 9,84 8,06 8,67 | 689,24 621,28 598,93 638,56 491,13 373,06 621,16 673,62 466,31 532,75 |
| Столбец 6 | Столбец 7 | Столбец 8 | Столбец 9 | Столбец 10 | |||||

| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| 8,98 8,43 9,04 10,60 9,63 10,97 8,77 9,07 8,91 10,38 | 568,23 506,65 575,46 773,63 646,83 824,15 543,87 579,56 560,95 743,22 | 9,31 9,29 9,04 10,13 9,68 8,66 8,88 9,43 8,81 8,20 | 608,14 605,72 576,15 710,49 653,68 531,79 557,32 622,92 548,98 480,97 | 10,43 8,97 9,18 10,33 10,04 9,14 10,22 9,10 8,25 8,66 | 750,59 567,78 592,59 736,87 699,34 587,48 723,08 583,02 486,95 531,98 | 9,68 10,50 9,51 9,88 8,16 8,98 8,13 7,21 9,33 10,60 | 653,25 759,24 631,76 679,17 476,74 568,97 474,10 381,13 610,68 774,19 | 8,99 9,13 9,14 10,25 6,84 8,72 10,35 8,12 9,94 7,41 | 570,25 586,56 587,68 726,99 346,08 538,49 739,89 472,21 686,47 400,57 |
2.1. Определение основных параметров случайных величин
 и
и 
Возьмем некоторые данные для случайной величины  из расчетно-графической работы №1. Интервальный ряд для СВ
из расчетно-графической работы №1. Интервальный ряд для СВ  :
:
| № п/п | Интервалы | Середина интервала
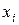
| Частота
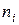
|
| [6,75; 7,18) | 6,97 | ||
| [7,18; 7,61) | 7,40 | ||
| [7,61; 8,04) | 7,83 | ||
| [8,04; 8,47) | 8,26 | ||
| [8,47; 8,9) | 8,69 | ||
| [8,9; 9,33) | 9,12 | ||
| [9,33; 9,76) | 9,55 | ||
| [9,76; 10,19) | 9,98 | ||
| [10,19; 10,62) | 10,41 | ||
| [10,62; 11,05) | 10,84 |
Среднее арифметическое наблюдаемых значений случайной величины X: 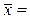 9,0548. Дисперсия
9,0548. Дисперсия 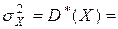 0,7988. Среднеквадратическое отклонение:
0,7988. Среднеквадратическое отклонение: 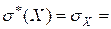 0,89.
0,89.
Используя критерий Пирсона, получаем, что случайная величина  распределена по нормальному закону.
распределена по нормальному закону.
Построим интервальный ряд для случайной величины  . Весь диапазон измерений признака
. Весь диапазон измерений признака 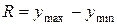 , где
, где  и
и 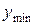 – соответственно максимальное и минимальное значение признака
– соответственно максимальное и минимальное значение признака  , разбивают на
, разбивают на 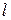 интервалов, где
интервалов, где 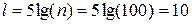 . Найдем оптимальную длину интервалов:
. Найдем оптимальную длину интервалов:
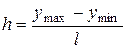 . ymax=824,15, ymin=338,21, h=(824,15–338,21)/10=48,6.
. ymax=824,15, ymin=338,21, h=(824,15–338,21)/10=48,6.
Получаем интервальный статистический ряд следующего вида:
| № п/п | Интервалы | Середины интервала | Частоты |
| [338,21; 386,81) | 362,51 | ||
| [386,81; 435,41) | 411,11 | ||
| [435,41; 484,01) | 459,71 | ||
| [484,01; 532,61) | 508,31 | ||
| [532,61; 581,21) | 556,91 | ||
| [581,21; 629,81) | 605,51 | ||
| [629,81; 678,41) | 654,11 | ||
| [678,41; 727,01) | 702,71 | ||
| [727,01; 775,61) | 751,31 | ||
| [775,61;824,21) | 799,91 |
Среднее арифметическое наблюдаемых значений случайной величины Y:
 =58023,80/100=580,238.
=58023,80/100=580,238.
Дисперсия:  =D*(Y)=
=D*(Y)=  =1112388,68/100=11123,8868. Среднеквадратическое отклонение:
=1112388,68/100=11123,8868. Среднеквадратическое отклонение: 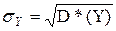 =105,4698.
=105,4698.
Проверим нулевую гипотезу о нормальном виде распределения 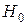 :
: 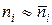 , где
, где 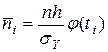 . Проверку гипотезы о виде нормального распределения можно провести с помощью критерия Пирсона
. Проверку гипотезы о виде нормального распределения можно провести с помощью критерия Пирсона 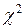 . Для чего нам потребуется следующая таблица:
. Для чего нам потребуется следующая таблица:
| yi | ni | yi– 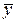
| 
| j(ti) | 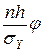 (ti) (ti)
| 
|
| 362,51 | 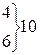
| –217,73 | –2,06 | 0,0478 | 2,2997 | 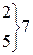
|
| 411,11 | –169,13 | –1,60 | 0,1109 | 5,3354 | ||
| 459,71 | –120,53 | –1,14 | 0,2083 | 10,0214 | ||
| 508,31 | –71,93 | –0,68 | 0,3166 | 15,2317 | ||
| 556,91 | –23,33 | –0,22 | 0,3894 | 18,7341 | ||
| 605,51 | 25,27 | 0,24 | 0,3876 | 18,6476 | ||
| 654,11 | 73,87 | 0,70 | 0,3123 | 15,0248 | ||
| 702,71 | 122,47 | 1,16 | 0,2036 | 9,7953 | ||
| 751,31 | 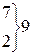
| 171,07 | 1,62 | 0,1074 | 5,1670 | 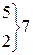
|
| 799,91 | 219,67 | 2,08 | 0,0459 | 2,2083 |
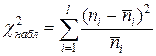 =
=

Найдем  , a – уровень значимости (a=0.05), n –число степеней свободы n=l–r–1. Так как l=8–2–1=5, то
, a – уровень значимости (a=0.05), n –число степеней свободы n=l–r–1. Так как l=8–2–1=5, то  (0.05,5)=11.1.
(0.05,5)=11.1.
Сравним 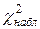 и
и  :
: 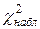 <
<  , следовательно, нет оснований отвергнуть гипотезу о нормальном распределении случайной величины Y.
, следовательно, нет оснований отвергнуть гипотезу о нормальном распределении случайной величины Y.
Дата добавления: 2016-02-24; просмотров: 573;
