Построение корреляционной таблицы

Построим корреляционную таблицу:

X Y	[6,75; 7,18)	[7,18; 7,61)	[7,61; 8,04)	[8,04; 8,47)	[8,47; 8,9)	[8,9; 9,33)	[9,33; 9,76)	[9,76; 10,19)	[10,19; 10,62)	[10,62; 11,05)	ny
6,97	7,40	7,83	8,26	8,69	9,12	9,55	9,98	10,41	10,84
[338,21; 386,81)	362,51												7,142	0,04438
[386,81; 435,41)	411,11												7,4
[435,41; 484,01)	459,71												8,1644444	0,03196
[484,01; 532,61)	508,31												8,4893333	0,04602
[532,61; 581,21)	556,91												8,9842105	0,03995
[581,21; 629,81)	605,51												9,2717647	0,04223
[629,81; 678,41)	654,11												9,636	0,02958
[678,41; 727,01)	702,71												10,0875	0,03467
[727,01; 775,61)	751,31												10,41
[775,61;824,21)	799,91												10,84
nx
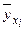
		362,51	394,91	459,71	484,01	529,1385714	579,185	633,2814	693,87364	736,73	799,91
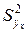
			524,88		590,49	578,4391837	586,389375	578,4392	351,36595	496,0116

2.3. Проверка однородности дисперсий случайных величин и по критерию Бартлетта

Проверим однородность дисперсий случайных величин и по критерию Бартлетта.

Проверим нулевую гипотезу, состоящую в том, что генеральные дисперсии случайной величины Y равны между собой.

.

Найдем дисперсию воспроизводимости 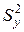по формуле (17).

В качестве критерия проверки нулевой гипотезы об однородности дисперсий примем критерий Бартлетта (18).

Критическую точку 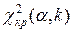находим по уровню значимости 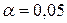и числу степеней свободы : .

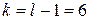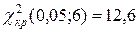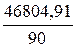=520,0545; 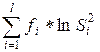=540,7162115;

V=(90 ln520,0545–234,8300669)=50,9834;

C=1+ 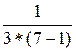0,674247492=1,037458;

B=50,9834/1,037458=49,14261.

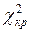Сравним и : – гипотеза об однородности дисперсий случайной величины Y отвергается.

Проверим однородность дисперсий случайной величины :

.

Найдем дисперсию воспроизводимости :

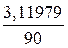= = 0,034664; 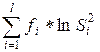=–260,372

V=(90 ln0,034664–(–260,372))= –97,2151

C=1+ 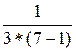(0,766504–1/90)=1,041966; B=–97,2151/1,041966=–40,5195.

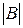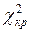Сравним и : – гипотеза об однородности дисперсий случайной величины отвергается.

Итак, обе величины и 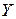имеют неоднородные дисперсии, т.е. экспериментальные данные получены некорректно. Вообще говоря, мы не имеем права продолжать работу по статистической обработке. Но в учебных целях перейдем к следующему пункту.