ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ОБЪЕКТОВ И ИХ АТРИБУТОВ

До сих пор мы занимались структурами данных, которые имеют мало общего с графическим представлением картографических или географических объектов. Хотя все три упомянутые системы могут использоваться для управления графикой, они мало что говорят нам о том, как сама графика будет представляться в ГИС. Мы знаем, что человеческий разум способен создавать графическое представление пространства и объектов в нем. Это представление в действительности довольно сложное, как вы увидите, когда мы попытаемся перейти к компьютерной реализации графических приемов. Главная трудность состоит в том, что наше графическое восприятие включает набор подразумеваемых отношений между элементами, расположенными на бумаге. Одни линии соединяются с другими линиями, и вместе они образуют области или многоугольники. Связь линий друг с другом в пространстве выражается посредством углов и расстояний. Одни линии замкнуты, другие - нет. Одни многоугольники имеют соседей, другие — изолированы. Список возможных взаимоотношений, которые могут содержаться в чертеже, практически бесконечен. Нам нужно найти способ представления каждого объекта и каждого отношения в виде набора явных правил, которые помогут компьютеру "понять", что все эти точки, линии и области представляют нечто на земле, что они находятся в определенных местах пространства и что эти места также связаны с другими объектами в пространстве. Мы можем даже захотеть объяснить компьютеру, что многоугольник имеет непосредственного соседа слева, и этот сосед может иметь с ним общие точки и линии. В общем, нам нужно создать язык пространственных отношений.

Существуют два основных метода представления географического пространства. Первый метод используетквантование (quantization), или разбиение пространства на множество элементов, каждый из которых представляет малую, но вполне определенную часть земной поверхности. Этотрастровый (raster) метод может использовать элементы любой подходящей геометрической формы при условии, что они могут быть соединены для образования сплошной поверхности, представляющей все пространство изучаемой области.

Хотя возможны многие формы элементов растра, например, треугольная или шестиугольная, обычно проще использовать прямоугольники, а еще лучше — квадраты, которые называются ячейками (grid cells). В растровых моделях ячейки одинаковы по размеру, но это не является обязательным требованием для разбиения пространства на элементы, которое не выполняется в не очень широко используемом подходе, называемом квадродеревом. В данном разделе мы рассмотрим модели, в которых все ячейки — одинакового размера, и представляют такое же количество географического пространства, как любые другие.

Растровые структуры данных не обеспечивают точной информации о местоположении, поскольку географическое пространство поделено на дискретные ячейки конечного размера. Вместо точных координат точек мы имеем отдельные ячейки растра, в которых эти точки находятся (Рисунок 4.9). Это еще одна форма изменения пространственной мерности, которая состоит в том, что мы изображаем объект, не имеющий измерений (точку), с помощью объекта (ячейки), имеющего длину и ширину. Линии, то есть одномерные объекты, изображаются как цепочки соединенных ячеек. Опять же, здесь имеет место изменение пространственной мерности от одномерных объектов к двухмерным структурам. Каждая точка линии представляется ячейкой растра, и каждая точка линии должна находиться где-то внутри одной из ячеек растра. Легко увидеть, что эта структура данных изображает линии ступенчатым образом (Рисунок 4.9). Этот ступенчатый вид также обнаруживается при изображении областей с помощью ячеек растра (Рисунок 4.9).

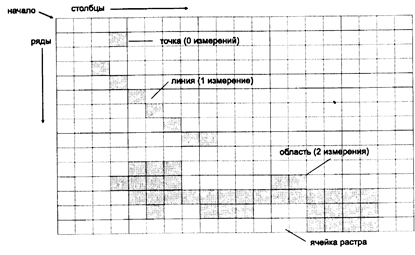
Рисунок 4.9. Растровое представление графики. Рисунок показывает точки, линии и области как объекты квантованного географического пространства. Растровые структуры не содержат точной координатной информации для таких объектов.

В растровых системах есть два способа включения атрибутивной информации об объектах. Простейшим является присваивание значения атрибута (например, класса растительного покрытия) каждой ячейке растра. Распределяя эти значения, мы в конечном итоге позволяем позициям значений атрибутов играть роль местоположений объектов. Например, если числом 10 мы представляем водную поверхность, и записываем его в левую верхнюю ячейку растра, то по умолчанию эта ячейка является участком земной поверхности, представляющем воду. Таким образом мы можем каждой ячейке на данной карте присвоить только одно значение атрибута. Альтернативный подход, а на самом деле, - расширение только что описанного, состоит в связывании каждой ячейки растра с базой данных, так что любое число атрибутов может быть присвоено каждой ячейке растра. Этот подход становится все более преобладающим, так как он уменьшает объем хранимых данных и может обеспечивать связь с другими структурами данных, которые также используют СУБД для хранения и поиска данных.

Хотя абсолютное местоположение не является явной частью растровой структуры данных, оно подразумевается относительным положением ячеек. Таким образом, линия представляется ячейками в определенных положениях относительно друг друга; области представляются смежными ячейками. Как вы могли догадаться, чем больше размер ячейки, тем большую площадь земли она покрывает, то есть, тем ниже (грубее)разрешение (resolution) растра, и тем меньше точность положений точек, линий и областей, представленных данной структурой.

Ячейки растра примыкают друг к другу для покрытия всей области. Благодаря этому мы можем использовать номера ячеек по вертикали и горизонтали в качестве координат, а также можем сопоставить с этими номерами обычные декартовы координаты (см. Главу 3). Как мы уже видели, системы прямоугольных координат используют картографические проекции для приблизительного изображения трехмерной формы участка земли. Ячеечное представление может иметь встроенную координатную систему, которая лучше аппроксимирует абсолютное положение, чем декартовы координаты. Например, пикселы изображений дистанционного зондирования (см. Главу 3) создаются в некоторой проекции, и для измерений на растре может помещена более точная координатная сетка. Однако в общем случае точные измерения на любой растровой структуре затруднены. Поэтому когда требуются точные измерения, растровые структуры используются реже, чем другие типы. ^

Растровые структуры данных могут показаться плохими из-за отсутствия точной информации о местоположении. На самом деле верно обратное. Растровые структуры имеют много преимуществ перед другими. В частности, они относительно легко понимаются как метод представления пространства. Возможно, некоторые из вас видели распечатки изображений героев мультфильмов на календарях, отпечатанных на АЦПУ и столь распространенных в 60-х и 70-х годах. Если нет, то вы уж наверняка знакомы с телевидением, которое использует то же растровое представление изображений. Немногие из нас имеют трудности в опознавании актеров по их изображениям на экране телевизора, даже несмотря на то, что все представлено набором точек (пикселов). В действительности, родство между пикселом, используемом в дистанционном зондировании, и ячейкой, используемой в ГИС, обеспечивает легкий перенос спутниковых изображений в ГИС, основанные на растре, не требуя каких-либо изменений. Это ~ еще одно преимущество растровых структур данных перед Другими. Еще одной замечательной характеристикой растровых систем является то, что, как вы увидите в Главе 12, многие функции, особенно связанные с операциями с поверхностями и наложением (overlay), легко выполняются на этом типе структур данных.

Среди главных недостатков растровой структуры данных - уже упоминавшаяся проблема низкой пространственной точности, которая уменьшает достоверность измерения площадей и расстояний, и необходимость большого объема памяти, обусловленная тем, что каждая ячейка растра хранится как отдельная числовая величина. Последняя проблема сегодня не так серьезна, как прежде, благодаря огромному росту емкости внешних запоминающих устройств компьютеров. Кроме того, как вы увидите позднее в этой главе, существуют методы уменьшения необходимого для хранения объема памяти, использующие упаковку групп ячеек растра в более компактные формы. Хотя объем памяти и не является теперь главным ограничением в использовании растровых структур, даже самые быстрые компьютеры могут быть загружены до состояния черепашьего хода вычислениями высокой сложности, выполняемыми на больших изображениях.

Второй метод представления географического пространства, называемый векторным (vector), позволяет задавать точные пространственные координаты явным образом. Здесь подразумевается, что географическое пространство является непрерывным, а не квантованным на дискретные ячейки. Это достигается приписыванием точкам пары координат (X и Y) координатного пространства, линиям - связной последовательности пар координат их вершин, областям - замкнутой последовательности соединенных линий, начальная и конечная точки которой совпадают (Рисунок 4.10).

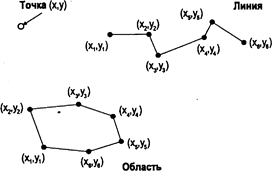
Рисунок 4.10. Векторное представление графики. Рисунок показывает точки как отдельные пары координат, линии - как группы пар координат, области - как соединенные линии с началом и концом в одной точке.

Векторная структура данных показывает только геометрию картографических объектов. Чтобы придать ей полезность карты, мы связываем геометрические данные с соответствующими атрибутивными данными, хранящимися в отдельном файле или в базе данных. Благодаря этому контурное изображение объектов становится больше похожим на карту. В растровой структуре мы записывали значение атрибута в каждую ячейку, в векторном же представлении мы используем совсем другой подход, храня в явном виде собственно графические примитивы без атрибутов и полагаясь на связь с отдельной атрибутивной базой данных.

В векторных структурах данных линия состоит двух или более пар координат. Для одного отрезка достаточно двух пар координат, дающих положение и ориентацию в пространстве. Более сложные линии состоят из некоторого числа отрезков, каждый из которых начинается и заканчивается парой координат. Для кривых линий может использоваться приближенное изображение с помощью большого числа коротких прямых отрезков. Чем короче отрезки, тем более точно они представляют сложную линию. Таким образом, мы видим, что хотя векторные структуры данных лучше представляют положения объектов в пространстве, они не абсолютно точны. Они все же являются приближенным изображением географического пространства.

Хотя некоторые линии существуют самостоятельно и имеют определенную атрибутивную информацию, другие, более сложные наборы линий, называемыесетями, содержат также дополнительную информацию о пространственных отношениях этих линий. Например, дорожная сеть содержит не только информацию о типе дороги и ей подобную, она показывает также возможное направление движения. Эта информация должна быть присвоена каждому отрезку, чтобы сообщить пользователю, что движение может продолжаться вдоль каждого отрезка до изменения атрибутов, возможно, до того момента, когда двухсторонняя улица станет односторонней. Другие коды, связывающие эти отрезки, могут включать информацию об узлах, которые их соединяют. Узел, например, может иметь знак останова, светофор или знак запрета разворота. Все эти дополнительные атрибуты должны быть определены по всей сети, чтобы компьютер знал присущие реальности отношения, которые этой сетью моделируются. Такая явная информация о связности (connectivity) и пространственных отношениях называетсятопологией (topology). Мы вернемся к этой теме, когда будем рассматривать векторные модели данных, которые мы можем создать на основе базовой векторной структуры данных.

Площадные объекты могут быть представлены в векторной структуре данных аналогично линейным. Соединяя отрезки линии в замкнутую петлю, в которой первая пара координат первого отрезка является одновременно и последней парой координат последнего отрезка, мы создаем область, или полигон (polygon)*. Как с точками и линиями, так и с полигонами связывается файл, содержащий атрибуты этих объектов.

*То же, что многоугольник в геометрии — прим. перев.

Вообще говоря, картографы предпочитают векторные структуры данных перед растровыми из-за их сходства с графическими структурами, чаще всего связываемыми с бумажными картами. За некоторыми исключениями, картографические документы, создаваемые на основе векторных структур данных, сильно напоминают нарисованные от руки карты. Только лишь вывод карт не является главной целью ГИС, но способность измерять и анализировать картографически организованные данные. А для этого необходим какой-то способ комбинирования графических объектов с их атрибутами. Мы упомянули в этой связи использование отдельных файлов с атрибутами и баз данных. Структуры данных должны разрабатываться так, чтобы обеспечивать эту связь, явно или косвенно. Кроме того, существуют многие другие характеристики графических структур, важные с точки зрения анализа карт. Мы должны перейти от простых структур данных к тому, что часто называютмоделями данных, которые больше похожи на карты в смысле способности участвовать в анализе. Мы рассмотрим некоторые их типы, как для растровых, так и для векторных структур.