Векторные модели данных

Как мы уже видели, векторные структуры данных дают представление географического пространства более интуитивно понятным способом и очевидно больше напоминают хорошо известные бумажные карты. Вы также помните, что они представляют пространственное положение объектов явным образом, храня атрибуты чаще всего в отдельном файле для последующего доступа. Существуют несколько способов объединения векторных структур данных в векторную модель данных, позволяющую нам исследовать взаимосвязи между показателями внутри одного покрытия или между разными покрытиями. Мы рассмотрим их на примере трех основных типов: спагетти-модели, топологической модели и кодирования цепочек векторов. Хотя существуют и другие типы, и многие варианты каждого типа, этих должно вам хватить для обзора того, что имеется для векторных ГИС.

Простейшей векторной структурой данных является спагетти-модель [Dangermond, 1982] (Рисунок 4.13), которая по сути переводит "один в один" графическое изображение карты. Возможно, она представляется большинством из нас как наиболее естественная или наиболее логичная, в основном потому, что карта реализуется как умозрительная модель. Хотя название звучит несколько странно, оно на самом деле весьма точно по сути. Если представить себе покрытие каждого графического объекта нашей бумажной карты кусочком (одним или несколькими) макарон, то вы получите достаточно точное изображение того, как эта модель работает. Каждый кусочек действует как один примитив: очень короткие — для точек, более длинные — для отрезков прямых, наборы отрезков, соединенных концами, - для границ областей. Каждый примитив — одна логическая запись в компьютере, записанная как строки переменной длины пар координат (X,Y).

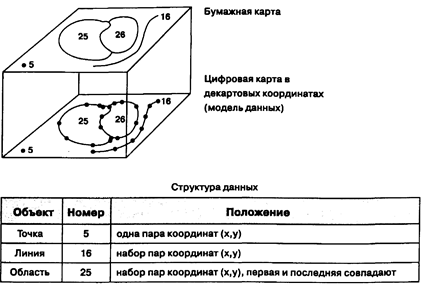
Рисунок 4.13. Спагетти-модель векторных данных. Нет явной топологической информации, модель — прямой перевод графического изображения.

В этой модели соседние области должны иметь разные цепочки спагетти для общих сторон. То есть, не существует областей, для которых какая-либо цепочка спагетти была бы общей. Каждая сторона каждой области имеет свой уникальный набор линий и пар координат. Хотя, конечно, общие стороны областей, даже будучи записанными отдельно в компьютере, должны иметь одинаковые наборы координат.

Поскольку спагетти-модель выглядит как перевод "один к одному" аналоговой карты, пространственные отношения между объектами (топология), например, такие, как положение смежных областей, -подразумеваются, а не записываются в компьютер в явном виде. И все отношения между всеми объектами должны вычисляться независимо. Результатом отсутствия такого явного описания топологии является огромная дополнительная вычислительная нагрузка, которая затрудняет измерения и анализ. Но так как спагетти-модель очень сильно напоминает бумажную карту, она является эффективным методом картографического отображения и все еще часто используется в компьютеризованной картографии, где анализ не является главной целью. Кроме того, это представление оказывается весьма близким к языку управления многих плоттеров, что упрощает преобразование и повышает его эффективность. Отрисовка на плоттере данных спагетти-модели обычно довольно быстрая по сравнению с другими.

В отличие от спагетти-модели,топологические модели [Dangermond, 1982] (Рисунок 4.14), как это следует из названия, содержат топологическую информацию в явном виде. Для поддержки продвинутых аналитических методов нужно внести в компьютер как можно больше явной топологической информации. Подобно тому, как математический сопроцессор объединяет многие специализированные математические операции, так и топологическая модель данных объединяет решения некоторых из наиболее часто используемых в географическом анализе функций. Это обеспечивается включением в структуру данных информации о смежности для устранения необходимости определения ее при выполнении многих операций. Топологическая информация описывается набором узлов и дуг.Узел (node) - больше, чем просто точка, обычно это пересечение двух или более дуг, и его номер используется для ссылки на любую дугу, которой он принадлежит. Каждаядуга (arc) начинается и заканчивается либо в точке пересечения с другой дугой, либо в узле, не принадлежащем другим дугам. Дуги образуются последовательностями отрезков, соединенных промежуточными (формообразующими) точками. В этом случае каждая линия имеет два набора чисел: пары координат промежуточных точек и номера узлов. Кроме того, каждая дуга имеет свой идентификационный номер, который используется для указания того, какие узлы представляет ее начало и конец.

Области, ограниченные дугами, также имеют идентифицирующие их коды, которые используются для определения их отношений с дугами. Далее, каждая дуга содержит явную информацию о номерах областей слева и справа от нее, что позволяет находить смежные области. Эта особенность данной модели позволяет компьютеру знать действительные отношения между графическими объектами. Другими словами, мы имеем векторную модель данных, которая лучше отражает то, как мы, пользователи карт, определяем пространственные взаимоотношения, записанные в традиционном картографическом документе.

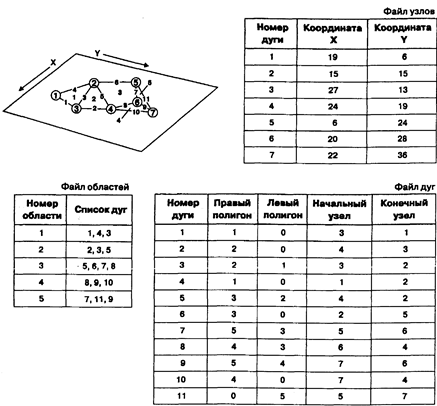
Рисунок 4.14. Топологическая векторная модель данных. Обратите внимание на включение явной информации о соединении узлов, дуг и областей.

Разработаны и применяются несколько топологических моделей данных. Все они немного различаются, и мы посмотрим на некоторые наиболее общие из них с тем, чтобы выяснить, как можно их реализовать. Возможно, наиболее известной является модельGBF/DIME (geographic base file/dual independent map encoding), созданная Бюро переписи США для хранения в компьютере уличной сети, используемой при переписях, проходящих каждые десять лет [U.S. Department of Commerce, Bureau of the Census, 1969] (Рисунок 4.15а). В ней дуги используются для представления улиц, рек, рельсовых путей и т.д. [Peuquet, 1984]. В этой топологической структуре данных каждая дуга заканчивается при смене направления или при пересечении с другой дугой (то есть, не используются промежуточные точки), а узлы идентифицируются кодами. Вдобавок к базовой топологической модели, GBF/DIME присваивает дугам коды направлений в форме пар Начальный узел - Конечный узел. Этот подход упрощает проверку потери узлов (см. Главу 6) при редактировании. Если, например, вы хотите посмотреть, не потерял ли контур полигона какие-либо дуги, просто проверьте совпадение начального узла каждой дуги с конечным узлом предыдущей дуги. Если где-то обнаружится несовпадение, то это значит, что какая-то дуга потеряна [Peuquet, 1984].

Дополнительным полезным свойством системы GBF/DIME является то, что для каждой дуги явно определены почтовые адреса и координаты UTM, что обеспечивает доступ к адресам через координаты. Однако, эту модель данных преследует та же проблема, что и базовую топологическую модель и, конечно, спагетти-модель тоже. Поскольку нет определенного порядка, в котором отрезки встречаются в системе, то чтобы найти какой-то конкретный отрезок, программа должна выполнить утомительный последовательный поиск по всей базе данных. А это самый медленный из возможных способов поиска. Более того, GBF/DIME основана на идее теории графов, где не важна форма линии, соединяющей любые две точки. Поэтому сторона многоугольника, используемая для обозначения извилистой границы реки, будет записана не как кривая линия, а как прямая между двумя точками, а результирующая модель не будет иметь графической точности, к которой мы привыкли, общаясь с бумажными картами.

Некоторые проблемы GBF/DIME были устранены с разработкой другой системы,TIGER (topologically integrated geographic encoding and referencing system) [Marx, 1986], созданной для использования в переписи США 1990 года (Рисунок 4.15b). В этой системе точки, линии и области могут адресоваться явно, поэтому участки переписи могут выбираться прямо по номеру участка, а не через информацию о смежности, содержащуюся в связях. Кроме того, так как эта модель не полагается не только на теорию графов, объекты реального мира, такие как извилистые реки и нерегулярная береговая линия отображаются графически более точно [Clarke, 1990]. Поэтому файлыTIGER полезны также и для исследований, не связанных с переписью.

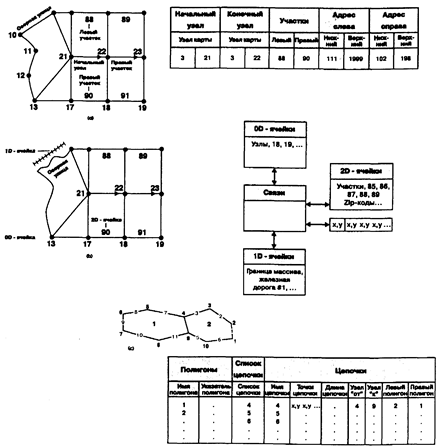
Рисунок 4.15. Топологические модели данных. Примеры топологических векторных моделей данных: а) GBF/DIME, b) TIGER, с) POLYVRT.

Еще одна модель, разработанная Пьюкером и Крисмэном [Peucker and Chrisman, 1975], и реализованная позже в Гарвардской лаборатории компьютерной графики [Peuquet, 1984], называетсяPOLYVRT (POLYgon conVeRTer) (Рисунок 4.15с). Как и TIGER, она устраняет неэффективность хранения и поиска, присущую базовой топологической модели, раздельным хранением каждого типа объектов (точки, линии, области). Эти отдельные объекты затем связываются в иерархическую структуру данных, где точки через указатели связаны с линиями, а линии — с областями. Каждый набор отрезков, называемый в данной моделицепочкой, начинается и заканчивается в определенных узлах (пересечениях двух цепочек). И, как и в GBF/DIME, каждая цепочка содержит явную информацию о направлении в форме "Начальный узел - Конечный узел", а также идентификаторы правых и левых областей (Рисунок 4.15с).

Как и TIGER, POLYVRT имеет преимущество отдельного хранения каждого типа объектов: вы можете выбрать точки, линии или области по желанию, идентифицируя их по кодам (которые, конечно, связаны с записями их атрибутов). Поскольку в POLYVRT списки цепочек, окружающие полигоны, хранятся в явном виде и связаны через указатели с каждым полигоном, размер БД определяется в большей степени числом полигонов, нежели сложностью их геометрических форм. Это повышает эффективность хранения и поиска, особенно в случае сложных полигональных форм, встречающихся у многих природных объектов [Peuquet, 1984]. Главный недостаток POLYVRT-это трудность обнаружения неверного указателя для заданного полигона пока он не будет реально выбран, и даже тогда вы должны точно знать, что этот полигон должен представлять.