Распознавание образов с применением минимаксного критерия

Минимаксный критерий используется для построения систем распознавания, когда априорные вероятности появления объектов соответствующих классов 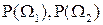неизвестны. В этом случае невозможно минимизировать средний риск и байесовская стратегия непосредственно неприменима.

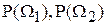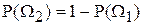Минимаксный критерий рассматривает наихудший вариант величин априорных вероятностей по отношению к величине среднего риска . Рассматривая классификацию на два класса, можно считать, что справедливо равенство: . Это равенство позволяет записать формулу для среднего риска (30.1) в виде функции от априорной вероятности. Типичный вид такой функции приведен на рис.25.1. Точки графика вычисляются путем решения уравнения байесовской стратегии (24.2) для каждого значения априорной вероятности .

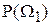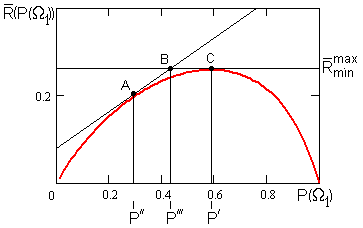
Рис.25.1. Зависимость среднего риска от априорной вероятности

Минимаксная стратегия соответствует точке С, выбор которой обеспечивает то, что при любом фактическом значении априорной вероятности 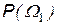средние потери не будут превышать 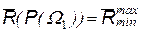. Значение порога минимаксного критерия определяется из уравнения:

.

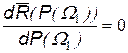Вычисление производных слагаемых среднего риска приводит к следующему уравнению:

.

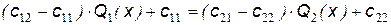Иногда используют упрощающие соотношения и обозначения: 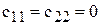, , 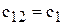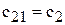. В таком случае уравнение для порога критерия минимакса имеет вид:

.

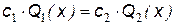Выбор иной стратегии, например стратегии, соответствующей точке А, приводит к тому, что на интервале 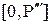средний риск меньше 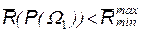, но на интервале 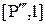потери будут больше гарантированного значения .

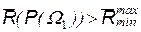Минимаксная стратегия есть байесовская стратегия для наихудших значений априорных вероятностей, дающая осторожное, но гарантированное значение среднего риска.