Пример определения пороговых значений для вероятностных алгоритмов распознавания
Заданы следующие функции условной плотности вероятности:
 ,
,
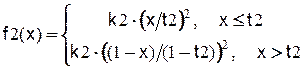 .
.
Параметры и константы этих функций имеют следующие значения:
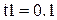 ,
, 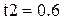 ,
, 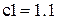 ,
, 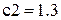 ,
, 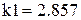 ,
, 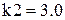 ,
, 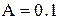 .
.
Графики функций 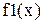 и
и 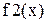 приведен на рис.28.1.
приведен на рис.28.1.

Рис.28.1. Графики функций условной плотности вероятности
С целью упрощения процесса поиска пороговых значений, параметры распределений подобраны так, что для всех критериев значения порогов находятся в интервале [x1,x2], поэтому в уравнениях используются правая ветвь функции f1(x) и левая - f2(x). Для критерия Байеса уравнение имеет вид: 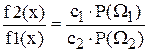 .
.
Подстановка численных значений и последовательные преобразования позволяют получить квадратное уравнение:
 ,
, 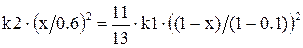 ,
,
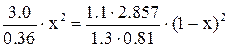 ,
, 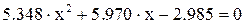 .
.
Решение квадратного уравнения дает следующее значение порога критерия Байеса: 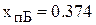 .
.
Уравнение для порога критерия минимакса имеет вид:
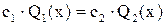 .
.
Подставив в это уравнение заданные функции получим:
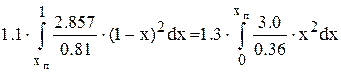 ,
,
 ,
, 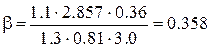 ,
,
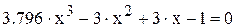 .
.
Решение кубического уравнения дает следующее значение порога критерия минимакса: 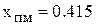 .
.
Уравнение для порога критерия Неймана-Пирсона имеет вид:
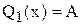 .
.
Подставив в это уравнение заданные функции, получим:
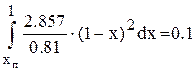 ,
,
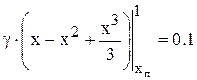 ,
, 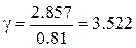 ,
,
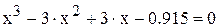 .
.
Решение кубического уравнения дает следующее значение порога критерия Неймана-Пирсона: 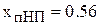 .
.
Дата добавления: 2016-02-16; просмотров: 854;
