Основные определения исчисления предикатов

Предикат – это высказывательная функция, определенная на некотором множестве М, то есть такая n-местная функция Р, которая каждому упорядоченному набору 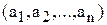элементов множества М сопоставляет некоторое высказывание, обозначаемое 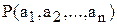[20].

Предикат – фундаментальное понятие математической логики, являющееся условием, сформулированным в терминах некоторого точного логико-математического языка. Предикат содержит обозначения для произвольных объектов – переменные. При замещении переменных именами объектов предикат задает точно определенное высказывание.

Предикат, имеющий одну переменную, называется свойством, а предикат с двумя переменными – отношением.

Исчисление предикатов первого порядка – формальный язык, выражающий разнообразные утверждения.

Правильно построенные формулы (ППФ) –допустимые выражения исчисления предикатов. Элементы формул: предикатные символы, символы переменных, функциональные символы, символы констант, символы логических операций.

Система продукций – обобщение вычислительного формализма, использующего предикаты и оперирующее понятиями: структура, класс, объект, свойства, правила.

Пример: 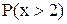- предикат, который имеет значение «истина», если 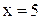. Если 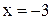, то предикат возвратит значение «ложь».