Система опровержения на основе резолюций
Правило построения резолюций позволяет формализовать процесс доказательства теорем [11]. Система доказательств использует метод доказательства от “противного”.
Дано: S - множество ППФ.
Доказать: W - целевая ППФ.
Алгоритм:
1) К множеству S добавляется отрицание ППФ W.
2) Расширенное множество преобразуется в множество предложений.
3) Ищется резолюция, представленная пустым предложением, т.е. соответствующая противоречию.
4) Если пустое предложение найдено, то теорема считается доказанной.
5) Если не удается получить резолюцию, соответствующую противоречию, то теорема считается не доказанной.
Пример 1: Имеются следующие утверждения:
1) Кто может читать, тот грамотный: 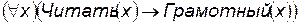 .
.
2) Дельфины не грамотны: 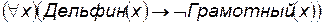 .
.
3) Некоторые дельфины обладают интеллектом: 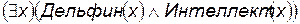 .
.
Требуется доказать: некоторые из тех, кто обладает интеллектом, не могут читать:  .
.
Множество утверждений соответствует следующим предложениям:
1) 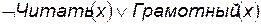
2) 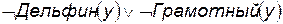
3) 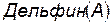 ,
, 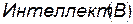 , где А, В – сколемовские константы.
, где А, В – сколемовские константы.
4) 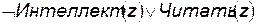 – отрицание доказываемой теоремы.
– отрицание доказываемой теоремы.
Процесс поиска противоречивой резолюции представляют в виде диаграммы, называемой деревом резолюций. Для рассматриваемого примера диаграмма представлена на рис.36.1. Базисное множество резолюций расположено в верхней строке диаграммы, а вычисляемые резолюции располагаются на более низких уровнях.
Рассматриваемое утверждение следует считать доказанным, так найдено пустое предложение. Верхняя строка диаграммы состоит из предложений базового множества. Вторая и все следующие строки принадлежат к различным уровням резолюций, номер уровня вершины дерева доказательств является одной из характеристик скорости получения доказательства.
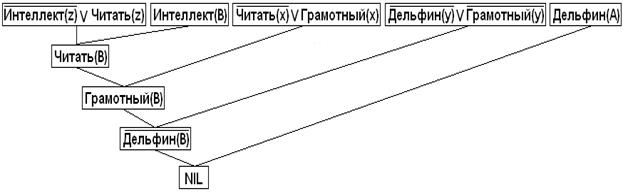
Рис36.1. Диаграмма вычисления резолюции
Пример 2: В Солнечном городе образованы три партии коротышек: винтиков, шпунтиков и болтиков. Оказалось, что для любых трех членов партий найдется партия, в которую входят двое из них. Верно ли, что все члены одной из партий являются членами какой-либо из двух других партий? (Данная логическая задача взята из журнала «Квант» №5, 2007 г.)
Обозначения:
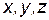 - имена конкретных коротышек,
- имена конкретных коротышек,
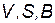 - название партий винтиков, шпунтиков и болтиков,
- название партий винтиков, шпунтиков и болтиков,
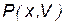 - двухместный предикат, определяющий принадлежность коротышки
- двухместный предикат, определяющий принадлежность коротышки 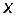 партии
партии 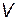 .
.
Задача состоит из двух высказываний, которые можно формализовать в виде следующих ППФ:
| 1) В Солнечном городе образованы три партии коротышек: винтиков, шпунтиков и болтиков. Оказалось, что для любых трех членов партий найдется партия, в которую входят двое из них. |
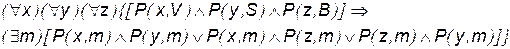
|
| 2) Верно ли, что все члены одной из партий являются членами какой-либо из двух других партий? |
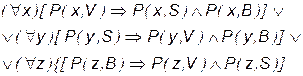
|
Второе высказывание является вопросом, поэтому его следует включить в базисное множество под знаком отрицания. Преобразование высказываний и отрицания вопроса во множество предложений дает следующие множества предложений:
1)
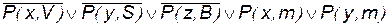 ; ;
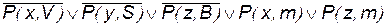 ; ;
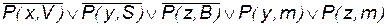 ; ;
|
2)
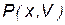 ; ; 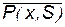 ; ; 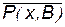 ; ; 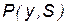 ; ; 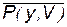 ; ; 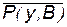 ; ;
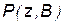 ; ; 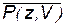 ; ; 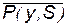
|
Базисное множество образовано 12 предложениями. Дерево доказательств приведено на рис.36.2. В дереве достаточно использовать 6 из 12 базисных предложений. Резольвенты одноместных предложений целевой функции и пятиместных предложений базисного множества позволяют последовательно, с ростом уровня вычисляемых резолюций, получать более короткие предложения. Имена констант важны и неизменны при вычислении резольвент.
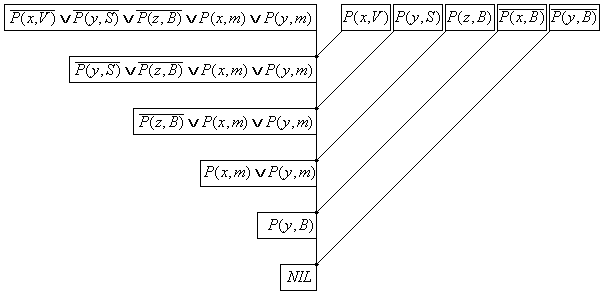
Рис.36.2. Дерево доказательств.
Второй пример демонстрирует, что пятиместные предикаты могут возникнуть при формализации довольно простых задач. Следует заметить, что шуточный характер примеров использован для более легкого восприятия условий и процесса решения задач, однако замена терминов легко переводит данные примеры в разряд технических задач. Второй пример может быть интерпретирован следующим образом:
«Механическая обработка деталей осуществляется тремя видами станков. Оказалось, что при обработке трех любых деталей, две детали обрабатывались на одном виде станков. Верно ли, что все детали, обработанные на одном из видов станков, были обработаны на одном из двух других видов станков?»
Дата добавления: 2016-02-16; просмотров: 1134;
