Моделирование процесса обучения нейронной сети

В данном разделе приводятся результаты моделирования процесса обучения нейронной сети методом обратного распространения ошибки в среде MahtCad. Рассматривается пример обучения распознаванию изображений трех символов.

Начальный этап моделирования: чтение эталонных изображений.

Векторизация и нормализация изображений к диапазону .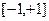

Собирание изображений в один вектор, каждая компонента которого – вектор.

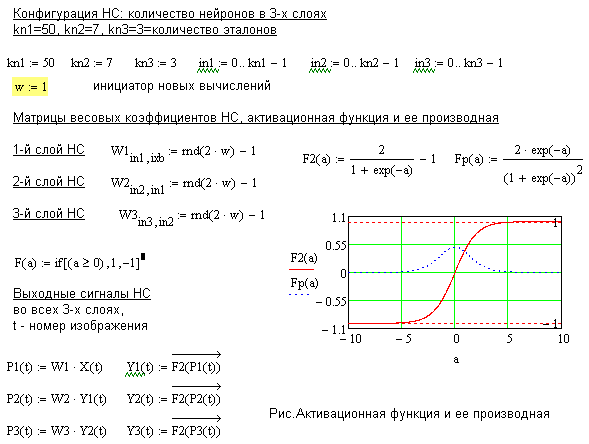
Формирование модели трехслойной нейронной сети. Матрицы весовых коэффициентов генерируются по равномерному закону распределения в интервале 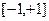. Определяется сигмоидальная активационная функция.

Множество правильных ответов на элементы обучающей выборки создается в виде вектора, количество элементов которого равно числу элементов обучающей выборки. Каждый вектор этого множества представляет собой вектор выходного сигнала НС, его длина соответствует числу нейронов выходного слоя. В программе используется пропозиционный код, то есть только один выход может находиться в состоянии «1», в то же время все остальные коды должны быть в состоянии «-1».

.

С целью проверки правильности формирования исходных матриц и векторов целесообразно провести контрольное вычисление прямого и обратного сигналов, формируемых нейронной сетью.

Программа обучения нейронной сети распознаванию изображений обучающей выборки вычисляет вектор, состоящий из 5-ти компонент: три матрицы весовых коэффициентов, матрицу изменения невязки и вектор выходных сигналов НС. Программу образуют два цикла: цикл 300 повторений процедуры обучения и цикл перебора изображений обучающей выборки.

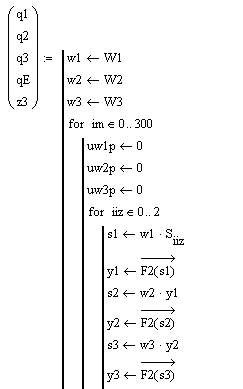
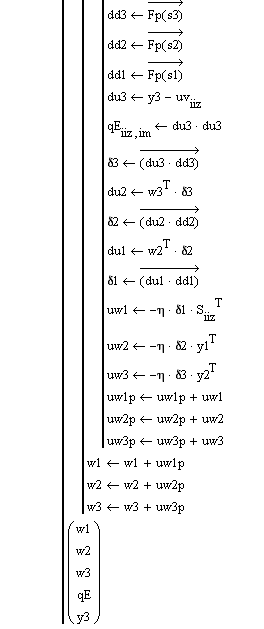
Программа обучения возвращает значения весовых коэффициентов, массив значений невязки и значения выходного сигнала. График изменения невязки в процессе обучения приведен ниже. Сплошная линия соответствует суммарной невязке по всем выходам НС. Из графика видно, что ошибка в процессе обучения уменьшилась в более чем 100 раз и составляет менее 1%.

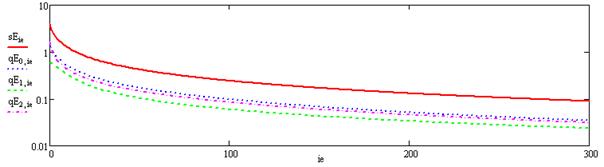
В приведенном ниже фрагменте программы формируется структура обученной нейронной сети – в ней используются матрицы весовых коэффициентов, полученных после завершения обучения.

Проверка правильности обучения может быть осуществлена путем построения карты выходных сигналов, которая приведена в следующем фрагменте моделирующей программы. Нейронная сеть работает правильно, если на всех выходах только по одному разу появляется единичный сигнал и моменты появления единиц не совпадают, то есть графики выходных сигналов образуют периодическую структуру. Дополнительным показателем завершенности процесса обучения является близость к «1» абсолютных величин выходных сигналов.

Пунктирными линиями соединены выходные сигналы до начала процесса обучения – они носят случайный характер.

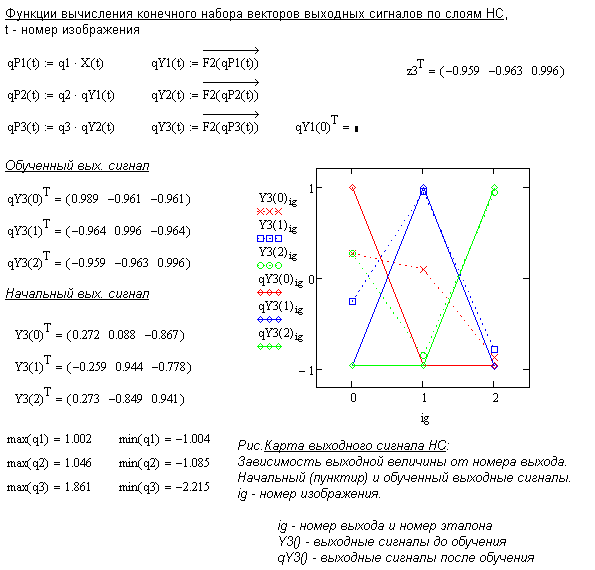
В программе выведены величины максимальных и минимальных значений весовых коэффициентов. Генерация начальных случайных величин весовых коэффициентов осуществлялась в интервале 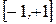, после обучения границы значений этих коэффициентов изменились несущественно.

Заключительной частью процесса моделирования служит эксперимент по предъявлению обученной НС ряда неизвестных изображений. В данном примере новые изображения синтезировались из двух эталонных: из первого изображения заимствовалось 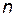верхних строк, а из второго – недостающие нижние строки. В рассматриваемом примере показаны изображения комбинированного символа с шагом в 5 строк.

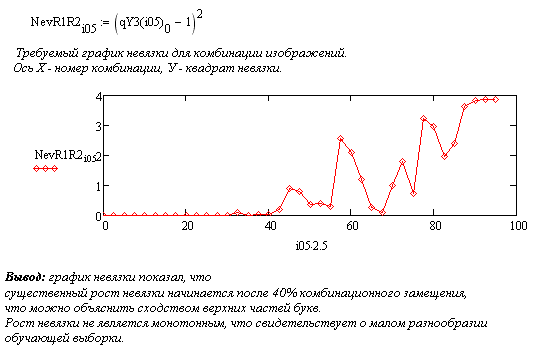
Результат работы НС можно оценить величиной суммарной невязки на выходе НС, график которой получен в последнем фрагменте моделирующей программы.

Заключительный эксперимент продемонстрировал свойство устойчивости НС к небольшим изменениям распознаваемого образа относительно эталонного изображения.

Приведенный пример модели НС может использоваться как образец для самостоятельного решения учебных заданий. Варианты заданий для самостоятельного выполнения приведены в следующем списке. Исследовать зависимость величины невязки на выходе обученной НС от следующих факторов:

· количества помеховых точек средней интенсивности;

· величины смещения символа по горизонтали в пределах изображения;

· интенсивности светлых точек изображения;

· количества удаляемых точек, образующих символ;

· интенсивности четных вертикальных линий изображения;

· величины контрастности верхней половины изображения.

Модель обучения НС может использоваться для поиска оптимальной величины коэффициента скорости обучения, способа генерации начальных значений весовых коэффициентов, конфигурации нейронной сети для решения конкретных задач распознавания символов или иных структур.