Уравнения гидростатики

Основное уравнение гидростатики, выражаемое часто в виде закона Паскаля, имеет ряд важных практических приложений; некоторые из них рассматриваются ниже.

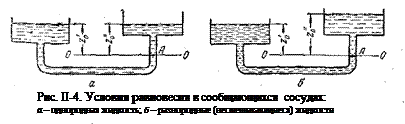
Принцип сообщающихся сосудов и его использование. Пусть два от­крытых сообщающихся сосуда (рис. II-4, а) заполнены жидкостью плотностью р. Выберем произвольно плоскость сравнения 0-0 и некоторую точку А внутри жидкости, лежащую в этой плоскости. Если считать точку А принадлежащей левому сосуду, то, согласно уравнению (II,18г), давление в данной точке

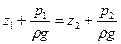(II,18)

Если же считать точку А принадлежащей правому сосуду, то давление в ней

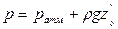
(z' = z" = 0, так как плоскость 0-0 проходит через точку А).

При равновесии для каждой точки давление одинаково в любом на­правлении (в противном случае происходило бы перемещение жидкости). Следовательно

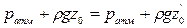
или

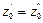(II,19)

Аналогичный вывод может быть сделан для двух закрытых сообщаю­щихся сосудов, в которых давления над свободной поверхностью жид­кости одинаковы.

Таким образом, в открытых или закрытых находящихся под одинаковым давлением сообщающихся сосудах, заполненных однородной жидкостью, уровни ее располагаются на одной высоте независимо от формы и попереч­ного сечения сосудов. Этот принцип используется, в частности, для измере­ния уровня жидкости в закрытых аппаратах с помощью водомерных стекол,

Если сообщающиеся сосуды заполнены двумя несмешивающимися жидкостями, имеющими плотности r' (левый сосуд) и r" (правый сосуд), то при проведении плоскости сравнения 0—0 через границу раздела жидко­стей (рис. II-4, б) аналогично предыдущему получим

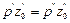(II,20)

или

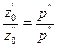(II,20a)

Отсюда следует, что в сообщающихся сосудах высоты уровней разно­родных жидкостей над поверхностью их раздела обратно пропорциональны плотностям этих жидкостей.

Если сосуды заполнены одной жидкостью плотностью r, но давления над уровнем жидкости в них неодинаковы и равны р' (левый сосуд) и р" (правый сосуд), то

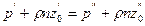
откуда разность уровней жидкости в сосудах

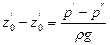(II,21)

Уравнение (II,21) применяют при измерениях давлений или разностей давлений между различными точками с помощью дифференциальных U-образных манометров.

Условия равновесия жидкостей в сообщающихся сосудах используют также для определения высоты гидравлического затвора в различных ап­паратах. Так, в непрерывно действующих сепараторах (рис. II-5) смесь жидкостей различной плотности (эмульсия) непрерывно поступает в ап­парат 1 по центральной трубе 2 и расслаивается в нем, причем более легкая жидкость плотностью r' удаляется сверху через штуцер 3, а более тяжелая имеющая плотность r", — снизу через U-образный затвор 4.

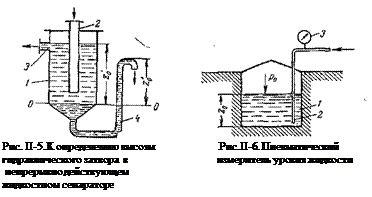
Если при­нять, что уровень границы раздела фаз поддерживается на границе ци­линдрической и конической частей аппарата и провести через эту границу плоскость сравнения 0-0, то необходимая высота гидравлического затвора, согласно уравне­нию (II,20), составит

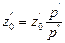(II,20б)

При этом допускается, что давление над жидкостью внутри аппарата и на выходе из затвора одинаково.

Пневматическое измерение количества жидкости в резервуарах. Для контроля за объемом жидкости в каком-либо резервуаре 1, например подземном (рис. II-6), в него помещают трубу 2, нижний конец которой доходит почти до днища резервуара. Давление над жидкостью в резервуаре равно р₀. По трубе 2 подают сжатый воздух или другой газ, постепенно повышая его давление, замеряемое манометром 3. Когда воздух преодолеет сопротивление столба жидкости в резервуаре и начнет барботировать сквозь жидкость, давление р, фиксируемое манометром, перестанет воз­растать и будет равно, согласно уравнению (II,18г)

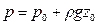
откуда уровень жидкости в резервуаре

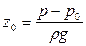(II,22)

По величине z₀ и известной площади поперечного сечения резервуара определяют объем находящейся в нем жидкости.

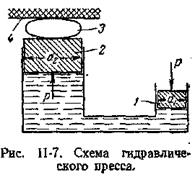Гидростатические машины. На использовании основного уравнения гидростатики основа-на работа гидростатических машин, например гид­равлических прессов (рис. II-7), применяемых в химической промышленности для прессования и брикети-рования различных материа­лов. Если приложить относительно небольшое усилие к поршню 1, дви­жущемуся в цилиндре меньшего диаметра d₁, и создать давление р на поршень, то, согласно закону Паскаля, такое же давление р будет при­ходиться на поршень 2 в цилиндре большего диаметра d₂. При этом сила давления на поршень 1 составит

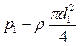
а сила давления на поршень 2

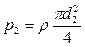
В результате поршень в цилиндре большего диаметра передаст силу давления, на столько большую, чем сила, приложенная к поршню в цилиндре меньшего диаметра, на сколько поперечное сечение цилиндра 2 больше, чем цилиндра 1. Таким способом с помощью сравнительно не­больших усилий осуществляют прессование материала 3, помещенного между поршнем 2 и неподвижной плитой 4.

Давление жидкости на дно и стенки сосуда. Если жидкость помещена в сосуд любой формы, то гидростатическое давление во всех точках гори­зонтального дна сосуда одинаково, давление же на его боковые стенки возрастает с увеличением глубины погружения.

Гидростатическое давление р на уровне дна сосуда (рис. II-3), как и для любой точки внутри жидкости, определяется уравнением (II,18г), но для всех точек дна величина (z₀ — z) представляет собой высоту жид­кости в сосуде. Обозначив последнюю через H, получим

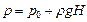(II,23)

Таким образом, сила давления P на горизонтальное дно сосуда не зави­сит от формы сосуда и объема жидкости в нем. При данной плотности жидкости эта сила определяется лишь высотой столба жидкости Н и пло­щадью F дна сосуда:

P = pF

или

P = (p₀ + rgH)F (II,24)

Гидростатическое давление, жидкости на вертикальную стенку сосуда изменяется по высоте. Соответственно сила давления на стенку также раз­лична по высоте сосуда. Поэтому

Р = (p₀ + rgh)F (II.24а)

где h — расстояние от верхнего уровня жидкости до центра тяжести смоченной пло­щади F стенки.

В уравнении (II,24а) выражение в скобках представляет собой гидро­статическое давление в центре тяжести смоченной площади стенки. По­этому сила давления на вертикальную стенку равна произведению ее смоченной площади на гидростатическое давление в центре тяжести смоченной площади стенки.

Точка приложения равнодействующей Р сил давления на стенку называется центром давления. Эта точка расположена всегда ниже центра тяжести смоченной площади. Если давление р₀ передается жидкостью в одинаковой степени каждому элементу стенки, независимо от глубины его погружения, и, следовательно, равнодействующая сила этого давления приложена в центре, тяжести стенки, то давление столба жидкости на стенку тем больше, чем глубже расположен соответствующий ее элемент. В результате, в частности, для вертикальной прямоугольной стенки центр давления расположен на расстоянии 2/3 Н от верхнего уровня жидкости.

ЛЕКЦИЯ 3